焊接变形三维摄影测量技术的研究

平 萍 白 泉

(1.太原重工煤化工分公司设计所，山西030024；2.太原重工铸锻分公司工艺所，山西030024)

在焊接构件的生产中，残余变形不仅影响结构的尺寸精度和外观，而且可能降低其承载能力和力学性能。矫正焊接变形费时、费工，甚至还会带来新的问题。因此，采取相应措施预测和减少变形对焊接结构质量的改进是十分重要的[1～6]。因此，国内外研究者都花费了大量的时间去设计各种方法对焊接变形进行测量。传统的焊接变形测量方法一般分为动态测量和静态测量两大类，区别是前者需要在测量变形的同时对温度加以测量；后者不需测量温度，可以直接得到变形量，但不能实时测量[7]。由于焊接是一个涉及到热、力、冶金等多学科的极为复杂的过程，因此要对其焊接变形进行准确模拟十分困难[8]。随着计算机和传感技术的发展，焊接变形的测量方法开始向自动化、智能化的方向发展[9，10]。其中，将三维摄影测量技术应用于焊接动态变形测量是一种较好的尝试。目前该方法已经较广泛的应用于材料力学试验当中，用于焊接变形测量则比较少见。本文基于摄影测量的原理，研究一种新的焊接变形动态测量的方法。

1 数字图像的自动处理

1.1 图像的获取

获取被测目标的影像是摄影测量的一个首要的基本过程。本文采用DH1302UM双目像机，如图1所示，其主要参数为1 280×1 024 pixel，CCD尺寸6.7 mm×5.3 mm。

图1 DH1302UM双目像机Figure 1 DH1302UM binocular camera

1.2 标志点的设计

数字近景摄影测量是一种基于图像的测量技术，一般都是通过处理被测物体图像中的特征目标(边缘、拐角点、十字刻划线、激光投射点或光条、圆形标志等)的影像，得到特征目标的二维图像坐标即对特征目标图像进行定位，然后进行测量。本文采用圆形作为基础形状来设计所需要的标志点。

对于非编码的标志点以一定半径的圆点(黑底白色或者白底黑色，图2所示)来实现就可以了，在使用中再去调整圆点的半径以使其适和场景的大小以保证精度。

对于编码的标志点必须设计一种确定的规则来约束使之能够正确识别解码。以白底黑色的编码点为例(图3)，其设计方案为：中心的黑色圆点总是不变用来计算编码点的圆心位置，而外圈的圆环则用来编码，编码的方式是把外圈等分成n(n为位数)个部分。

1.3 标志点的自动检测识别

本文采用的椭圆中心定位流程如图4所示。

图2 两种非编码标志点Figure 2 Two kinds of non-coded mark point

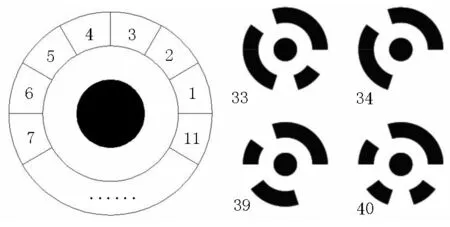
图3 编码点示意及实例Figure 3 The schematic diagram and example of coded mark points

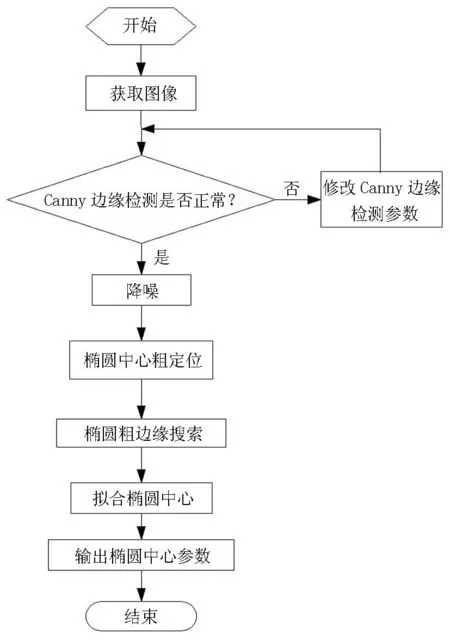
图4 椭圆中心定位的流程图Figure 4 The flow diagram of ellipse centering

对于编码点的检测，则需要在上述椭圆检测的基础上进行进一步的操作。由已经得到的椭圆参数，在每个椭圆长轴的2.8倍处构造一个新椭圆(见图5)。然后估算所构造的新椭圆边界大致包含的像素数量，根据像素数量计算步进角度，每个步进角度应包含2～5个边界像素。最后根据步进角度计算细分数量。

在实际的应用中，通过处理灰度图而得到一个由0和1组成的序列。另外，在每一个步进角度，在大小不同的同心椭圆上采了三个点(图6所示)，再由这三个序列通过一定的处理，得到一个和它们有相同容量的序列，通过这个序列经过进一步的处理，最终得到编码序列。

最后，根据上面所得到的序列，找到这个序列在循环移位过程中的最小值，得到它的编码，再根据设计时编码和实际编号之间的关系查表计算实际编号。

图5 编码点周围构造新椭圆Figure 5 Building new ellipse around coded point

图6 编码点周边采样Figure 6 Sampling around coded point

1.4 像点的系统误差

根据像机的成像原理，物点经过透镜摄影后成像在一个平面上，理想的透镜成像可以简化为一个小孔成像的数学模型。事实上，像机在制造过程中不可避免的会有镜头畸变、装配误差等，因此实际上得到的图像并不是物体的完美投影，特别是采用广角镜头时这种情况更是明显。任一像点的系统性误差是径向畸变、偏心畸变、像平面内畸变和内方位元素不准确引起的畸变的总和，这些内部参数所引起的像点坐标偏差称之为像点的系统误差，写成下式：

2 像机的标定

像机自标定是指仅通过像机运动所获取的图像序列来标定内部参数，而不需要任何的外部控制点，因而更加灵活，适用于在线测量。

本课题组采用自制的如图7所示的标定板，该标定板上所有的标志点坐标均为未知，只有斜对角两对编码点的距离为已知。用双目像机从不同角度拍摄8次照片。通过图像检测算法得到标志点的图像坐标和编码标志点的编号之后，采用10参数模型，利用自标定算法对该像机进行标定计算，得到像机的10个内参数。标定误差为0.035像素，两像机间的夹角为28.23°。

图7 实验所用标定板Figure 7 Calibration plate used for test

在对数字像机标定之后可以根据误差公式对获取的图像进行校正，调整使其更加接近于理论上的投影成像。

3 三维重建

假如能得到物体表面所有点的三维坐标，则三维物体的形状与位置就是唯一确定的。在有些简单的场合，如三维物体是个多面体，我们只需要知道它的各个顶点的三维坐标与相邻关系，则该多面体的形状和位置也是唯一确定的。因此，用立体视觉方法获取三维点的坐标是最基本的，也是最简单的，称为基于点的三维重建。

立体视觉技术是指通过对同一物体从不同角度获得的两幅图像来恢复出被摄物体的三维信息(尤其是物体的深度信息)的过程。如图8所示，根据实物点P在一幅图像中的像P1和摄像机的光心仅能确定一条经过P的投影射线O1P，O1P上的任何一点在图像1上的像点均为 P1。如果存在另一条与 O1P 不重合的投影射线经过P，则P在射线O1P上的位置就可以确定了。

摄影测量的基本成像模型是针孔模型。在成像模型满足针孔模型假设的前提下，像点、光心和物点满足共线方程，即三点共线。对于单像机的情况，如果光心和像点已知就可以确定像点和光心组成的唯一射线，而物点必然在此射线上。但是物点在此射线上的具体位置无法确定，就是说在没有其他附加信息的条件下，仅用单个像机的单幅图片是无法确定目标的三维位置的。

点的三维重建至少需要该点的两个投影，在已知图像坐标的前提下，再得到两幅图像的拍摄方位，就能计算出物体在物方空间直角坐标系中的三维坐标。

图8 立体视觉原理Figure 8 The principle of stereoscopic vision

4 实验及结果分析

采用上述动态变形测试系统对不锈钢薄板和普通低碳钢薄板TIG堆焊的焊接变形进行了测试。实验采用200 mm×160 mm×0.8 mm规格的板。焊接参数：焊接电流40 A；焊接电压11 V；焊接速度分别为30 cm/min和25 cm/min；氩气流量为8 L/min。3个位移传感器位于距焊缝中心60 mm的点1、2、3处(如图9所示)。

焊件的另一面布置编码点或者非编码点，如图10所示。

实验结果如图11所示。

图11中第一点变形情况为：前2 min内基本没有变形，可能是由于焊件本身就有比较大的初始变形，而且焊接速度较快，焊接热影响区较窄，

图9 位移传感器布置示意图Figure 9 The schematic diagram for displacement transducer arrangement

图10 编码点和非编码点布置Figure 10 The arrangement of coded and non-coded points

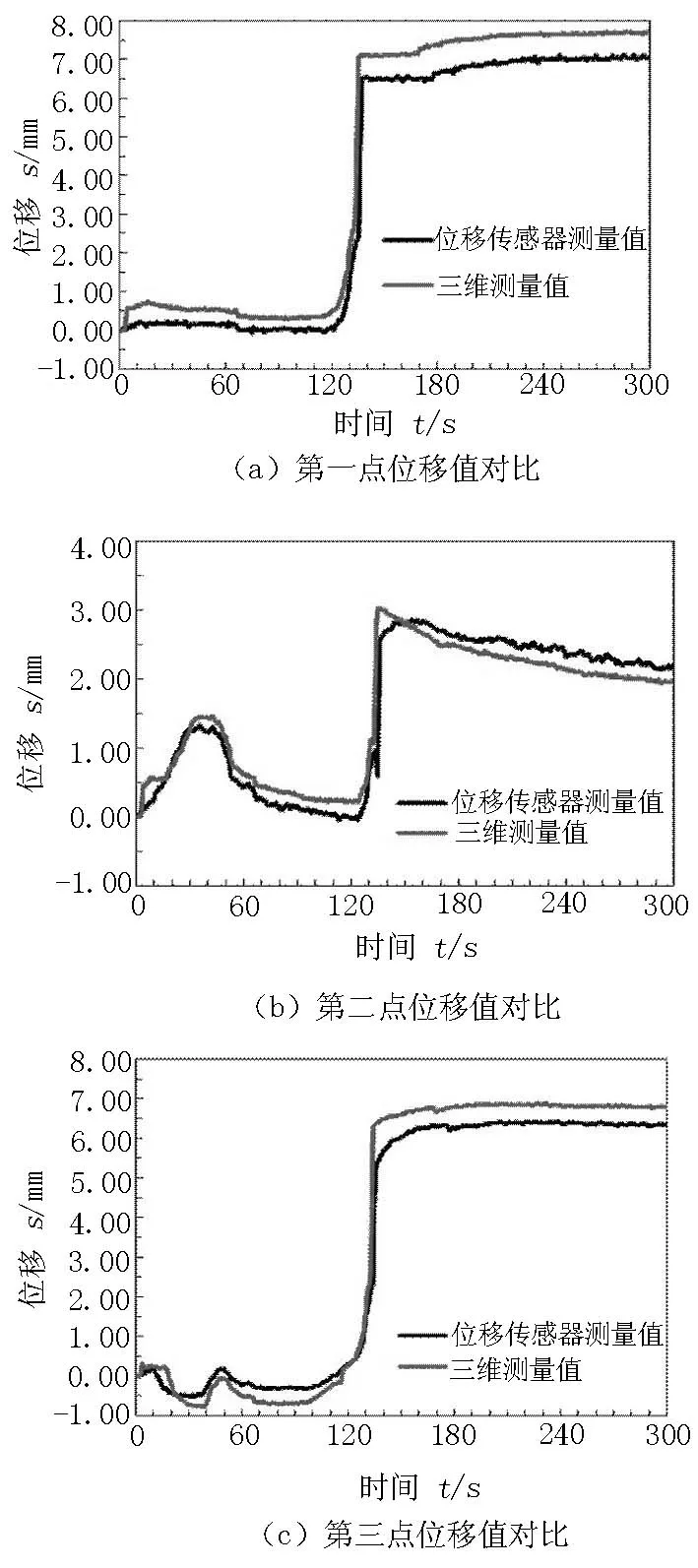
图11 实验1位移值对比Figure 11 The comparison of displacemen values for test 1

对第一点的影响不大所致。在135 s左右突然产生很大的变形，几秒钟之后变形就趋于稳定，这是由于焊接的残余变形突然释放的结果；第二点变形情况为：在前40 s内，随着时间的延续，焊件产生一个角变形，反映在2点处即该点变形逐渐变大。之后角变形逐渐释放，所以40 s后到130 s内，变形又逐渐减小。之后突然产生很大的变形，几秒钟之后变形就趋于稳定，与第一点的情况相同；第三点变形的情况基本同第一点，不同的是前2 min左右内变形较第一点稍大，可能是由于焊接方向是由下往上，焊接热量首先传到第三点，所以对第三点的影响较为明显的缘故。

图12 实验2位移值对比Figure 12 The comparison of displacemen values for test 2

图12中这三点的变形情况都是随着时间的延长，变形逐渐增大，到最大值之后开始减小，随后减小到某一固定值后趋于稳定。这是由于焊接速度较小，焊件产生了较大的角变形，随后的冷却过程中，这种角变形又稍微释放一点，稳定在一个固定值处。由于焊件上下两端与中间位置处释放的变形量不同，所以最终焊件是角变形与弯曲变形的复合变形。

从以上两个实验可以看出，三维摄影测量系统的测量值与位移传感器的测量值基本趋于一致，说明三维摄影测量系统可以很好的应用于焊接变形的动态测量。

三维摄影测量系统由于采用的是非接触式测

图13 实验1不同时刻焊件的变形云图Figure 13 The deformation cloud charts of weldment for test 1 under different moment

图14 实验2不同时刻焊件的变形云图Figure 14 The deformation cloud charts of weldment for test 2 under different moment

量，因此可以避免接触式测量的很多缺点。此外三维摄影测量系统还可以根据不同时刻各点的变形值得到焊件整个面的动态变形云图。由本实验数据近似计算得到的几个时刻的变形云图见图13和图14。

从图13中可以看出，实验1的60 s时刻焊件的四个边角都略为上翘，中间下凹，大致符合初始角变形与小弯曲变形复合变形的情况；134 s时刻焊件上下两端位移最大，左右两边位移次之，中间位移较小，符合大弯曲变形与角变形复合变形的情况。其余云图也都与实验过程中观察到的焊件变形一致。

5 结论

试验结果证明，该三维测量系统可以很好的应用于焊接变形的动态测量中，并且可以获得焊件不同时刻的变形云图。从而为焊接变形的动态测量提供了一种新的方法。

[1] 张建强，赵海燕，吴廷，等.焊接过程三维应力变形数值模拟研究进展[J].焊接学报，2003，24(5)： 91-96.

[2] 刘川，张建勋.基于动态子结构的三维焊接残余应力变形数值模拟[J].焊接学报，2008，29(4)：21-24.

[3] SAA Akbari Mousavi, R Miresmaeili. Experimental and numerical analyses of residual stress distributions in TIG elding process for 304L stainless steel[J]. Journal of Materials Processing Technology, 2008, 208: 383-394.

[4] Dean Deng, Hidekazu Murakawa. FEM prediction of buckling distortion induced by welding in thin plate panel structures[J]. Computional Materials Science, 2008, 43: 591-607.

[5] Dean Deng. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects[J]. Material and Design, 2009, (30): 359-366.

[6] Dean Deng, Wei Liang, Hidekazu Murakawa. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements [J]. Journal of Materials Processing Technology, 2007, 183: 219-225.

[7] 阮星谊，包晔峰，石忠贤.焊接变形测量方法[J].电焊机，2005，35(5)：55-57.

[8] 徐琳，严仁军.T形焊接接头残余应力与变形的三维数值模拟[J]. 江苏船舶，2007，24(1)：5-8.

[9] 王蕊，张建勋，肖克民，等.焊接变形与热循环动态测试系统开发[J].焊接设备与材料，2006，35(4)：37-39.

[10] 王蕊，张建勋，梁振新.新型焊接变形与热循环动态测试系统[J].焊接，2006(1)：27-30.