复Loeb测度空间中的Radon-Nikodym定理

史艳维，陈文利，冯晶晶

（西安培华学院 基础部，陕西 西安 710125）

复Loeb测度空间中的Radon-Nikodym定理

史艳维，陈文利，冯晶晶

（西安培华学院 基础部，陕西 西安 710125）

在非标准多饱和模型下，讨论了复 Loeb测度空间中的 Radon-Nikodym定理．首先，给出了复测度及其变差相应的Loeb测度之间的关系．其次，给出了有限测度的复Loeb空间中的Radon-Nikodym定理．最后，得到了σ-有限测度的复Loeb空间中的Radon-Nikodym定理．

复Loeb测度空间；绝对连续；Radon-Nikodym定理

自20世纪60年代，美国数学家Robinson A创立了非标准分析理论以来[1]，非标准分析的理论和应用得到了不断的发展[2-4]．作为以数理逻辑和模型论为基础的新兴的数学分支，非标准分析为其他数学方向的研究提供了新的方法和新的思路．1975年，Loeb P在文献[5]中应用非标准饱和模型，提出了一类以内集为支集的测度空间理论，即 Loeb测度，现在已经广泛地应用于测度扩张、测度表示等许多领域，是近年来非标准分析理论最活跃的研究方向之一．

本文在非标准多饱和模型下，讨论了复Loeb测度空间中的Radon-Nikodym定理．给出了复测度及其变差相应的Loeb测度之间的关系．并得到了有限测度和-有限测度的复Loeb空间中的Radon-Nikodym定理．本文总假设非标准模型V(*S)是多饱和模型．

设(Y,A,ν)是一个内有限可加复测度空间，ν=ν′ +iν ′，其中ν′和ν′是(Y,A)上的内有限广义测度．令L(A,ν)=L(A,ν′)∩L(A,ν′)，νL=+′，则复测度空间(Y,L(A,ν),νL)称为关于(Y,A,ν)的复Loeb空间，简记为(Y,L(A,νL)．

特别地，设(X,A,μ)是一个复测度空间，由转换原理， (*X,*A,*μ)是内有限可加复测度空间，其相应的复Loeb空间为(*X,L(*A),(*μ)L)．

定理1 设(Y,A,ν)是内有限可加复测度空间，则

(1) L(A,ν)=L(A,|ν|)．

(2) 对于任意的A∈L(A,ν)，|ν|L(A)=|νL|(A)．

证明 (1) 因为L(A,ν)=L(A,ν′)∩L (A,ν′)，于是L(A,ν′)=L(A,|ν′|)，L(A,ν′)=L(A,|ν′|)，所以L(A,ν)=L(A,|ν′|)∩L (A,|ν′|)．对于任意的A∈L(A,ν)，则A∈L(A,|ν′|)且A∈L(A,|ν′|)，由Loeb测度的定义，对于任意的ε＞0，存在Cn,Dn∈A，En,Fn∈A使得Cn⊆A⊆Dn，En⊆A⊆Fn且，

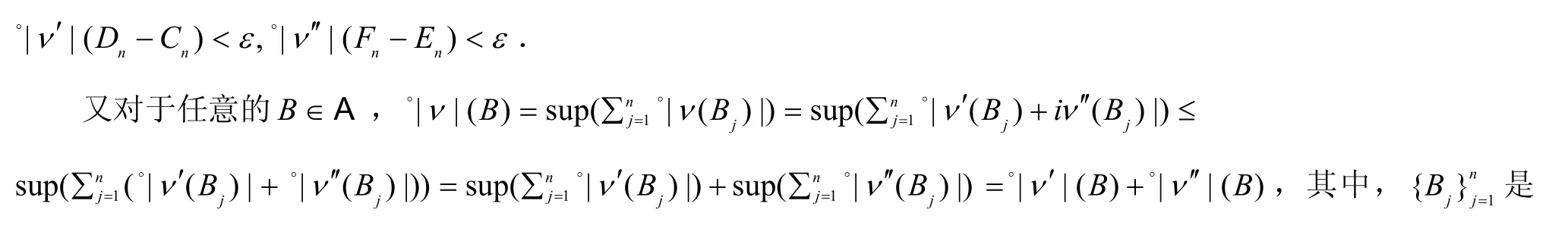
下面的定理称为复Loeb空间中的Radon-Nikodym定理．

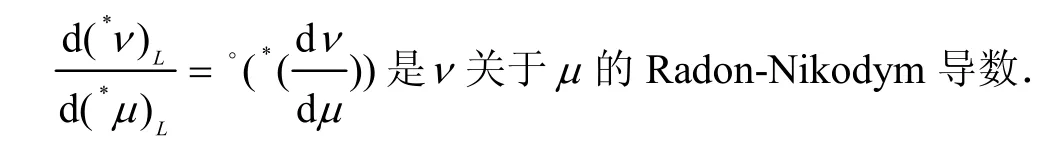
至此，z值已不能再改进．即得最优解：maxz=8,x*=（x1,x2,x3）=（1,0,1）．

比较表 1与表 2，显然表 2的计算判断次数明显少于表1的计算判断次数，表2总共只计算判断了12次．而表1总共要计算判断24次．

通过实例分析比较，我们可以得出这样一个结论：隐枚举法和改进的隐枚举法在对同一个问题的求解中，解的结果是完全相同的．但是，改进的隐枚举法在实际运用中却凸现了比隐枚举法更加方便快捷的优越性，表现在：对隐枚举法的第一步进行改进，即对于目标函数为最大(小)化的，我们若从目标函数中 xj的系数为正(负)的变量都取 1而其他变量都取 0开始试探，就会发现下面步骤的运算次数会大大减少，本文例 1使用了2种方法进行求解，大家明显可以看到使用改进的隐枚举法求解时确实大大地减少了运算次数，并且在运算次数大大减少的同时，还提高了运算的精确度．也体现了这种方法在推动实际工作实践中的有效性．

表2 改进后的判断过程

Abstract:This paper, from a perspective of contrastive analysis, has researched into the improvement of the Implicit Enumeration Method in applying the 0-1 Integer Programming in the Linear Programming. Practical examples have proved that the improved method is faster and feasible.

Key words:the 0-1 Integer Programming; the Implicit Enumeration Method; the improved enumeration

(责任编校：李建明英文校对：李玉玲)

Reflections on Improving the Implicit Enumeration Method

CHENG Hong-ping1; ZHAO Yin-feng2

(1. Teaching Office of Mathematics, Xi’an Eurasia University, Xi’an, Shaanxi 710065, China;
2. Siemens Signaling Company Ltd. Xi’an, Shaanxi 710016, China)

O141.41

A

1673-2065(2011)01-0012-03

2010-08-05

陕西省自然科学基金资助项目(2007A12); 西安培华学院校级课题资助项目(PHKT029201011)

史艳维(1980-),女,陕西西安人,西安培华学院基础部教师,理学硕士.