最小二乘外推与ARIMA(P,1,0)组合模型在极移短期预报中的应用*
2011-09-20张昊王琪洁朱建军张晓红
张昊 王琪洁 朱建军 张晓红
(中南大学地球科学与信息物理学院测绘与国土信息工程系,长沙410083)
最小二乘外推与ARIMA(P,1,0)组合模型在极移短期预报中的应用
*
张昊 王琪洁 朱建军 张晓红
(中南大学地球科学与信息物理学院测绘与国土信息工程系,长沙410083)
将ARIMA(P,1,0)模型应用到极移随机性部分序列的预报中,提出了利用最小二乘外推与ARIMA(P,1,0)的组合模型来对整体极移序列进行短期预报。并与其他方法对极移1~5天的短期预报精度进行了对比,结果证明了该模型在极移短期预报上的有效性与优越性。
极移;短期预报;最小二乘外推;ARIMA(P,1,0)模型;精度改善
AbstractThe necessity of the short-term prediction of polar motion and the current common prediction approach are discussed.ARIMA(P,1,0)is used in prediction of stochastic components in polar motion before,non a combinational model of least squares extrapolation and ARIMA(P,1,0)is given to forecast the polar motion from one to five day in the future.Through accuracy analysis,the efficiency and superiority of this model is proved.
Key words:polar motion;short-term prediction;least squares extrapolation;ARIMA(P,1,0)model;accuracy improving
1 引言
极移(PM)是指地球瞬时自转轴在地球本体内运动而导致极点在地球表面上的位置发生缓慢变化的现象。对于极移的预报,许多学者建立了各种预报模型对其进行研究[1-8]。总的来说这些模型都是将极移分成有规律的确定性部分及不规律的随机性部分分别进行预报。极移中有规律的确定性部分包括极移的长期趋势(LT)、钱德勒摆动(CW)、周年摆动(AW)和半周年摆动(SAW)。各种预报模型对这部分大都采用最小二乘对已有极移数据进行拟合,得出确定性的拟合模型,然后对其进行外推预报。极移中不规律的随机性部分是指极移中除去确定性部分而剩余的部分,很多文献也将之称为确定性模型残差,这一部分主要包括极移数据中周期低于半年的项及其他高频摆动项,极移中的这一部分振幅和相位变化极不规律,具有很大的随机性,对于这部分的预报不同的模型采用不同的预报方法,主要有人工神经网络(ANN)模型[2]、模糊推理系统(FIS)[3]、平稳自回归(AR)模型[4]等。极移最终的预报结果为确定性部分的外推值与随机性部分的预报值之和。现代测地技术对极移的测定精度可达到0.1毫角秒级[4],而以上方法对极移1~5天的短期预报精度却远远小于这一量级。本文提出利用最小二乘外推与ARIMA(P,1,0)组合方法对极移进行短期预报,经过实验分析得出:相对于其他方法,该方法对极移1~5天的短期预报精度有显著地提高。
2 预报方法
利用ARIMA(P,1,0)模型对极移随机性部分进行预报,利用最小二乘拟合的方法对极移确定性部分进行外推预报。
2.1 最小二乘外推模型
对极移中的确定性部分,用最小二乘外推模型进行外推预报。对于极移的X分量PX和Y分量PY,最小二乘外推模型的数学表达式为[5,6]:
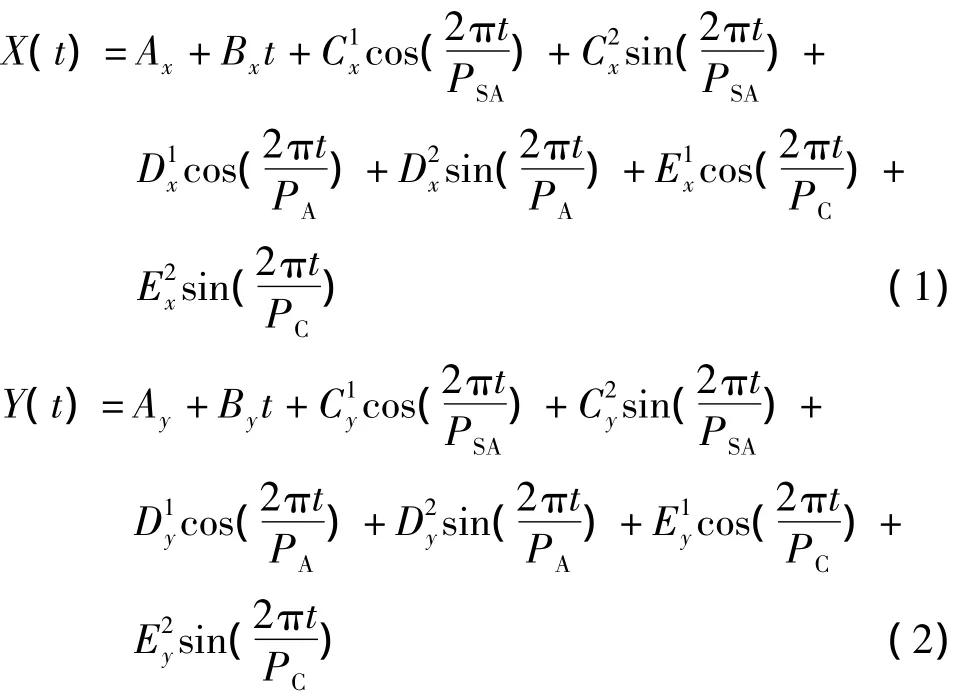
其中Ax、Bx表示极移X序列模型中LT参数,C1x、C2x表示极移X序列模型中SAW参数,D1x、D2x表示极移X序列模型中AW参数,E1x、E2x表示极移X序列模型中CW参数;PSA表示SAW周期,在拟合中取PSA=0.5年;PA表示AW周期,在拟合中取PA=1年; PC表示CW周期,在拟合中取PC=1.183年;t为序列的UTC时间,在进行拟合时单位换算为年。同样对于极移Y序列模型,各对应参数表示含义与X序列模型一样。
模型中各参数的求解是通过对已有极移数据序列进行最小二乘拟合而得到的。如图1(a)为1990-01-01—2010-11-23日的PX原始观测序列,图1(b)为该段时间内根据式(1)而得到的PX的最小二乘拟合序列,即极移观测序列中确定性部分序列。
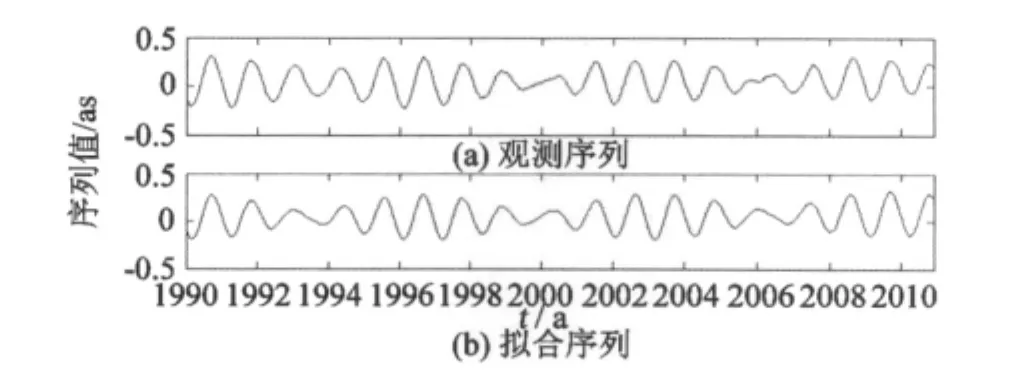
图11990 -01-01—2010-11-23PX序列Fig.1Observed series and fitted series of PX from 1990-01-01 to 2010-11-23
2.2 ARIMA(p,1,0)模型
ARIMA模型全称为求和自回归移动平均模型。该模型实质是d阶差分运算和ARMA(p,q)模型的结合。模型参数中d表示对原始时间序列进行差分的阶数,p为AR模型阶数,q为WA模型的阶数。ARIMA(p,d,q)进行预报的基本思想是:先对原始时间序列进行d阶差分,然后对差分后的时间序列运用ARMA(p,q)进行预报,最后对预报值进行差分逆运算得到原始时间序列的预报值[9-11]。
图2(a)为1990-01-01—2010-11-23日PX确定性模型残差序列,即PX中随机性部分,它是由原始观测序列与最小二乘模型拟合序列相减而得到。由图2(a)可以看出,模型残差序列两端波动较大,中间比较平缓,这是由拟合模型的本身性质而导致的:拟合模型在对原观测序列进行拟合时,在数据两端是发散的。本文在对该部分利用ARIMA进行预报时,取d=1,即对确定性模型残差序列进行一阶差分(图2(b))。
对于ARMA(p,q)模型,当p=0时,模型可表述为MA(q),即q阶移动平均模型;当q=0时,模型可表述为AR(p),即p阶自回归模型。对于一个时间序列,判断符合哪个模型,可借助该时间序列的自相关函数和偏相关函数,判定准则如表1[12]。
对模型残差一阶差分序列分别求时间延迟为1~40天的自相关函数与偏相关函数的结果见图3。
从图3可以发现对于PX序列,其确定性模型残差一阶差分序列的自相关函数具有拖尾性,偏相
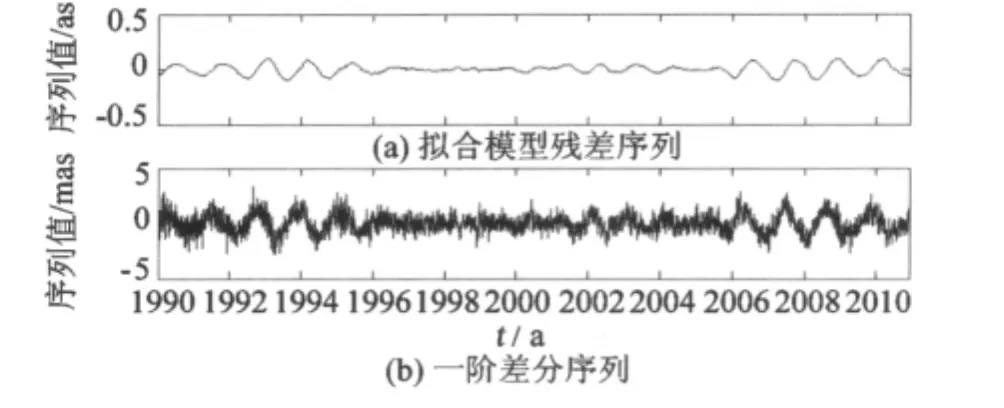
图21990 -01-01-2010-11-23PX序列Fig.2Residual series of fitting model and the first order differenced series from 1990-01-01 to 2010-11-23
关函数具有截尾性,故可采用AR(p)模型进行预报,即q=0。
AR(p)模型的数学模型为:
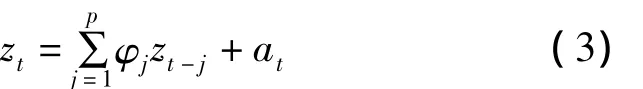
式中,zt(t=1,2,3,…,n)表示时间序列,在实际预报中代表确定性模型残差一阶差分序列。φ1,φ2,…,φp为模型参数,at表示白噪声,p为模型阶数。对于模型阶数p的确定,采用最终预报误差准则,其数学表达式为:
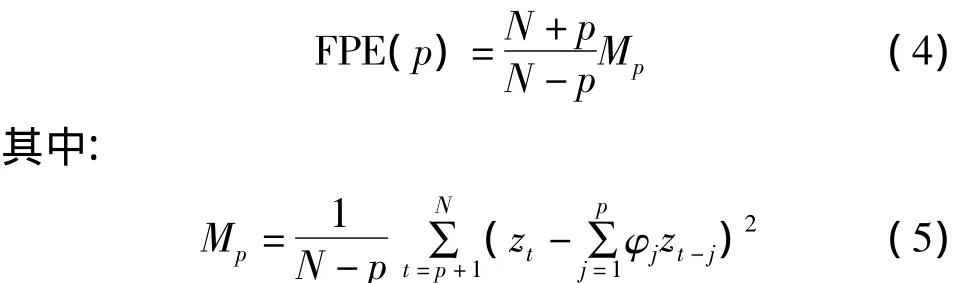

表1 时间序列模型判定准则Tab.1Judgement criterion of time series model
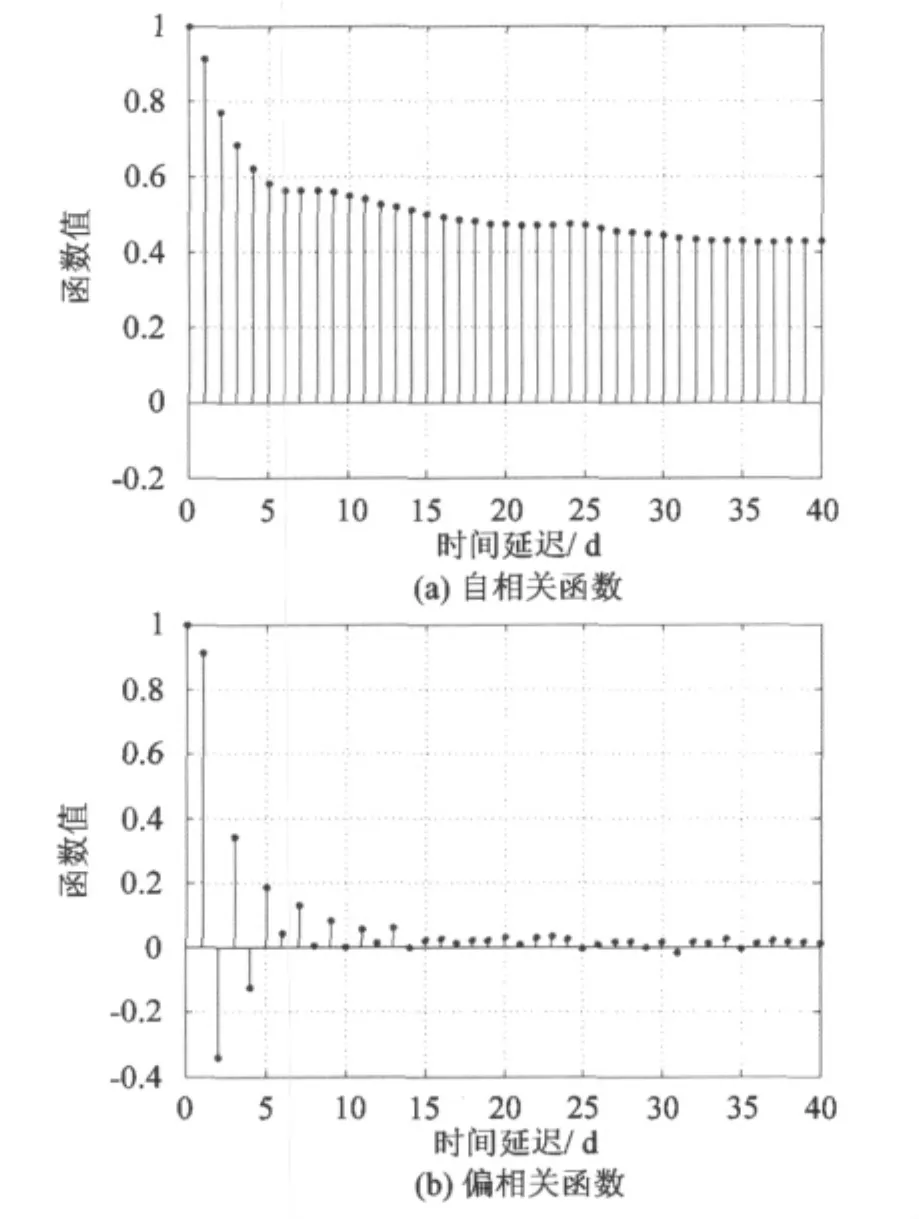
图3 差分序列时间延迟为1~40天的自相关函数与偏相关函数Fig.3Autocorrelation and partial correlation function of the difference series in time-delay from 1 to 40 days
在实际预报中,Mp是用AR(p)模型拟合zt(t= 1,2,3,…,n)序列的剩余均方差。当p=1,2,…,N时使FPE(p)达到最小时的p取作模型的阶。对AR模型参数φ1,φ2,…,φp的求解,采用李文逊[13]递推算法。
对于PX确定性模型残差序列,取参数d=1,q =0,即ARIMA(p,1,0)进行预报;PY序列与PX序列具有同样的性质,对于其确定性模型残差序列同样采用ARIMA(p,1,0)进行预报。
2.3 精度评定指标
采用均方误差(RMSE)作为精度评定指标,其计算式为:
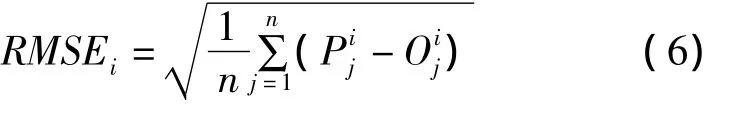
其中,Pj为j点的预报值,Oj为j点的实际值,i为预报跨度,RMSE-i为预报跨度为i的均方误差。
3 实验分析
为检验最小二乘外推与ARIMA(p,1,0)组合模型在极移短期预报上的有效性与优越性,用本文提出的方法与极移预报的其他方法进行对比,即在相同的特定时间段内做跨度1~5天的极移短期预报,然后分别统计其预报精度。
如表2,方法一为最小二乘外推与AR(p)组合模型[4],方法二为本文提出的最小二乘外推与ARIMA(p,1,0)组合模型,预报精度统计为2000年1月1日至2010年11月23日的统计值。其中极移综合预报精度由式(7)计算:
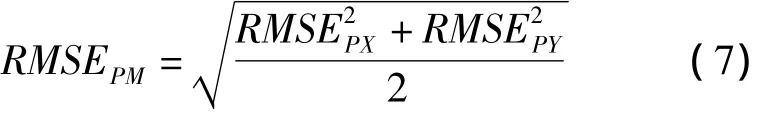
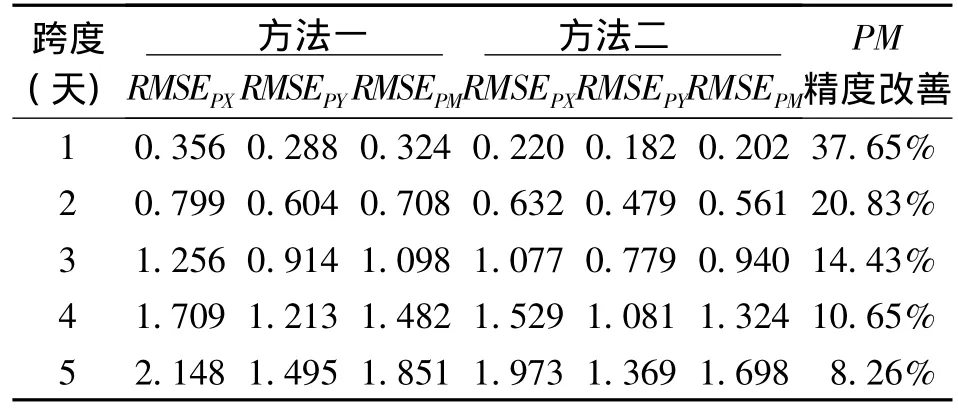
表21 -5天预报精度统计(单位:mas)Tab.2Comparison of prediction accuracy from 1 to 5 days(unit:mas)
从表2可以看出,本文提出的最小二乘外推与ARIMA(p,1,0)组合模型相对于最小二乘与AR(p)组合模型在极移短期预报精度上有较显著的改善。尤其是对于跨度为1天的预报,其精度改善达到近38%。随着跨度增加,精度改善的强度也在减弱。
另外我们还将本文提出的模型与最小二乘外推与ANN组合模型进行了对比。Schuh是对1999年到2000年内700个预报值作的精度统计[4],并且只给出了极移综合预报精度,为使实验对比更加客观,我们利用本文提出的方法与其进行对比时,精度统计也为相同周期内的同样个数的预报值。两种方法1-5天短期预报精度统计结果见表3。
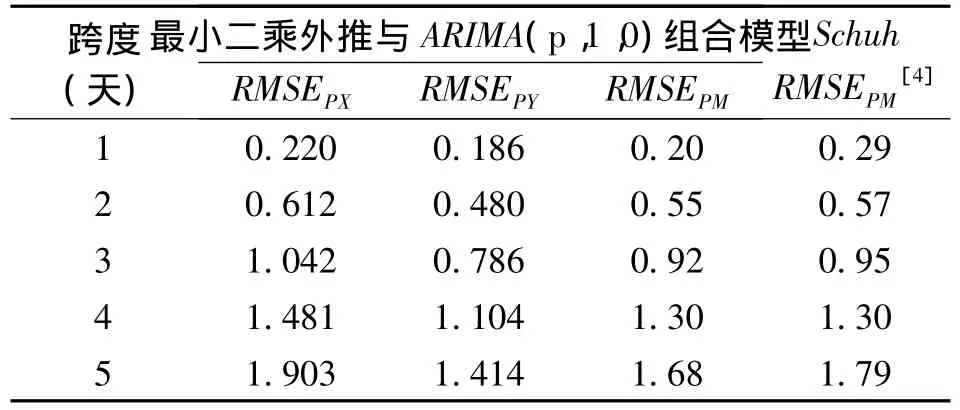
表3 在1999—2000时间段内1~5天预报精度统计(单位: mas)Tab.3Comparison of prediction accuracies from 1 to 5 days in the future between this approach and Schuh’approach during 1999—2000(unit:mas)
从表3可以看出,本文提出的方法相对于Schuh提出的模型在极移1~5天的短期预报精度上也有一定的改善,只有跨度为4天的预报值综合精度与Schuh的一样,而其他跨度均高于Schuh的预报精度。
4 总结与展望
利用最小二乘外推与ARIMA(p,1,0)组合模型对极移进行短期预报,其中对极移的确定性部分,采用最小二乘外推模型进行预报,而对极移随机性部分的预报方法利用ARIMA(p,1,0)对极移随机性部分进行预报。实验分析可以发现,本文的这一尝试在极移短期预报中具有有效性和优越性。
在实验中发现随着预报跨度的增加,本文的预报方法相对于另外两种方法对预报精度的改善强度在逐渐减弱,甚至在10~30天的短期预报中,其预报精度并不如另外两种方法,这说明了本文的预报方法只适合于极移短期预报。
1王琪洁.基于神经网络技术的地球自转变化预报[D].中国科学院上海天文台,2007.(Wang Qijie.Studies on the prediction of Earth’s variable rotation by Artificial Neural Networks[D].Shanghai Astronomical Observatory,Chinese Academy of Sciences,2007)
2Schuh H,et al.Prediction of Earth orientation parameters by artificial neural networks[J].Journal of Geodesy,2002,76:247-258.
3Akyilmaz O and Kutterer H.Prediction of Earth rotation parameters by fuzzy inference systems[J].Journal of Geodesy,2004,78:82-93.
4Kosek W,et al.Comparison of polar motion prediction results supplied by the IERS sub-bureau for rapid service and predictions and results of other prediction methods[A].In A Finkelstein and N Capitaine(eds.).Proc.journes systemes de reference spatio-temporels2003“Astrometry,geodynamics and Solar system dynamics:from milliarcseconds to microarcseconds”[C].St.Petersburg:Inst.of Applied Astronomy of the Russian Acad.of Sciences.2004.
5Zhu SY.Prediction of Earth rotation and polar motion[J].Bull Geod.,1982,56:258-273.
6Chao B F.Predictability of the Earth’s polar motion[J].Bull Geod.,1985,59:81-93.
7McCarthy DD and Luzum BJ.Prediction of Earth orientation[J].Bull Geod.,1991,65:18-21.
8徐军毅.基于截距修正的GM(1,1)模型在极移预测中的应用[J].大地测量与地球动力学,2010,(1):88-91.(Xu Junyi.GM(1,1)model based on intercept correction and application to polar motion prediction[J].Journal of Geodesy and Geodynamics,2010,(1):88-91)
9刘军,等.基于ARIMA(p,1,1)的电离层预报模型[J].大地测量与地球动力学,2010,(3):79-82.(Liu Jun,et al.A Predicting model of ionospheric based on ARIMA(p,1,1)[J].Journal of Geodesy and Geodynamics,2010,(3): 79-82)
10田铮.时间序列的理论与方法[M].北京:高等教育出版社,2001.(Tian Zheng.Time series:Theory and methods[M].Beijing:China Higher Education Press,2001)
11潘虹宇.时间序列分析[M].北京:对外经济贸易大学出版社,2006.(Pan Hongyu.Time series analysis[M].Beijing:University of International Business and Economics Press,2006)
12刘大杰,等.实用测量数据处理方法[M].北京:测绘出版社,2000.(Liu Dajie,et al.Practical measurement data processing method[M].Beijing:Surveying and Mapping Press,2000)
13丁月蓉.天文数据处理方法[M].南京:南京大学出版社,1998.(Ding Yuerong.Astronomical data processing methods[M].Nanjing:Nanjing University Press,1998)
APPLICATION OF COMBINATIONAL MODEL OF LEAST SQUARES EXTRAPOLATION AND ARIMA(P,1,0)IN SHORT-TERM PREDICTION OF POLAR MOTION
Zhang Hao,Wang Qijie,Zhu Jianjun and Zhang Xiaohong
(Department of Geomatics Engineering,Central South University,Changsha410083)
P207
A
1671-5942(2011)03-0106-04
2011-02-12
国家自然科学基金委员会与中国科学院天文联合基金(10878026);中南大学研究生学位论文创新基金
张昊,男,1987年生,硕士研究生,主要研究方向为GPS变形监测及现代测量数据处理.E-mail:zhanghao198706@gmail.com
