超大断面铁路隧道施工断面综合荷载释放过程研究

李术才，赵 岩,2，李利平，周 毅，刘 钦

（1. 山东大学 岩土与结构工程研究中心，济南 250061；2. 青岛市地下铁道公司，山东 青岛 266071）

1 引 言

近年来随着我国交通基础设施建设事业的大规模跨越式发展，我国西部地区所修建的大型公路、铁路工程数量不断增加。许多自然环境恶劣，地质条件复杂，以往被认为是“工程禁区”的地区都兴起了大规模的交通基础设施。山区基建工程的发展就使许多长大隧道工程不断涌现，尤其是在铁路工程建设中，考虑到造价等各项因素，当前的铁路隧道主要采取单洞双线的设计形式，隧道开挖断面较大，与此同时，工程建设难度及风险也进一步增加。与地面建筑物不同，隧道是修筑在具有一定应力历史和一定初始应力场的围岩中的结构物。初始应力场是在隧道开挖之前就已经客观存在的[1－5]。因此，隧道开挖的扰动会使一定范围内的围岩发生松弛，产生一定的荷载作用于隧道结构上。隧道开挖断面的加大，会增加隧道开挖的扰动范围和增加隧道结构所承受的荷载。根据岩承理论的思想，隧道洞壁围岩不仅仅是荷载的来源，更是隧道承载结构的重要组成部分，这里所说的隧道结构，不仅指狭义上的隧道支护结构，也包括在隧道开挖过程中发挥承载作用的洞壁围岩。随着隧道掌子面的推进，隧道结构所承受的荷载在围岩应力调整的过程中是不断释放的，最终开挖结束且隧道结构及围岩达到稳定状态后荷载的释放过程结束。而该荷载释放的演化过程则受到断面开挖方式、支护时机等多种因素的影响，可以认识到的是，平缓并且较少突变的荷载释放过程对隧道围岩损伤最小，同时也最有利于隧道结构的稳定。这样就可以通过对施工过程中的荷载释放规律进行研究，从而进一步分析施工过程中的围岩稳定性[6－9]。隧道施工的荷载释放过程一直是隧道施工力学的研究热点之一，许多专家学者通过数值分析或现场监测的手段对其进行过深入的研究，然而过去的研究往往只是针对隧道洞壁的一点展开，没有对开挖过程中某断面的整体荷载释放状态进行全面的研究。

本文通过数值分析及模型试验，对超大断面铁路隧道施工过程中的断面整体荷载释放过程进行了相关研究。首先，有针对性的研究了台阶法施工过程中隧道洞壁不同特征点的荷载变化规律，在此基础上定义了能够表征隧道断面整体荷载释放状态的断面综合荷载释放率和荷载释放差异系数概念，然后，分析总结了隧道开挖过程中的变化规律。随后通过隧道开挖过程地质力学模型试验的方法，监测开挖过程中洞壁不同位置的围岩径向压力变化过程，进一步说明了将整个断面作为一个整体研究对象的必要性，对断面整体荷载释放状态进行评价，有利于得出更适用性的结论，进而综合评估分析隧道施工过程中的荷载释放规律。

2 工程背景

本次研究以贵广铁路天平山隧道为工程背景。贵广铁路天平山隧道，位于广西壮族自治区桂林市，全长14 005 m，最大埋深为775 m，设计为双线单洞隧道，设计时速250 km，预留进一步提速条件。本隧道设置 0～4#斜井，6个工作面，是贵广铁路的控制性工程。图1为天平山隧道台阶法开挖断面情况。

图1 天平山隧道台阶法开挖断面Fig.1 The section of Tianpingshan tunnel

由于铁路客运专线的设计时速较高，故采用单洞双线隧道的设计形式有利于缓解行车过程中的隧道空气动力学问题。单洞双线隧道的开挖断面面积在150 m2左右，施作衬砌后的净空也在100 m2左右，属于超大断面隧道，开挖面积和净空面积的增大，导致了隧道施工过程中结构承受的围岩荷载的进一步增加。故对超大断面隧道施工中的荷载释放过程进行深入研究就有了重要的现实意义。

3 计算模型建立

数值计算方法是当前岩土工程研究中主要采取的重要手段之一，是试验手段和现场监测的有力补充，数值计算的研究不受监测点布置及测量精度的影响，有利于揭示施工过程中荷载变化过程的内在规律。

本研究使用基于拉格朗日方法的有限差分软件FLAC3D作为数值模拟手段。其计算原理遵循连续介质假设，通过每一个时步的计算积分求解，并且在计算的过程中节点与单元的坐标随着变形的增加而不断更新，能够求得介质的大变形，有利于贴近岩土工程问题的现实情况。参考地质条件及隧道实际断面设计情况，并对计算模型进行适当简化，首先，确定计算模型模拟范围：设水平方向为x轴，长度为80 m，纵向为z轴，沿隧道轴线方向30 m，竖直方向为y轴。由于计算中隧道断面及顶部荷载均为对称布置，故取隧道结构的1/2进行建模计算。所建立模型如图2所示。

数值计算屈服准则的选取是否科学是计算结果能否反映客观规律的基础，Mohr-Coulomb准则由于其能够反映岩土材料屈服时与球应力和偏应力密切相关的重要特性而在岩土工程研究中被广泛应，同时在计算中也要考虑到岩体的弹塑性变形及大变形[10－11]。计算过程中为了尽量减少模型体边界对计算结果产生的影响，主要提取开挖至计算模型中间时的计算数据。

图2 数值计算模型Fig.2 Model for numerical analysis

4 隧道施工荷载释放过程数值分析

隧道台阶法开挖是当前隧道施工中应用最广泛的方法，其具有施工效率高、工作平台空间大、方便机械化施工，并且具有可以多作业面平行作业等优点，并且在地质条件发生变化时，能够灵活及时地转换施工工序，调整施工方法[12]。

在台阶法施工过程中，围岩会受到开挖过程的多次影响，在台阶法开挖过程中，围岩应力状态转换过程的影响因素非常多，包括台阶开挖面积、长度、开挖循环进尺以及支护封闭成环距离等都对其有着重要的影响。本文选取上下台阶高度相同，台阶长度均为5 m的二台阶法开挖的标准工况作为研究对象。在台阶法施工荷载释放过程研究分析中，主要将拱顶处的竖向应力、边墙处的水平应力以及底板处的竖向应力作为研究对象。在分析过程中采用数据归一化处理的方法，消去应力的单位和方向，着重分析其数值上的变化过程。将每一步开挖结束后的径向应力的绝对值与初始地应力情况下进行对比，进而研究洞壁围岩径向应力的变化过程。图 3为监测点位置与隧道台阶分界线位置示意图。

图3 隧道台阶法开挖示意图Fig.3 Bench method excavation of the tunnel

图4为台阶法施工过程中隧道洞壁径向应力变化过程曲线图。其中，曲线的纵坐标为台阶法开挖到某一时刻隧道洞壁上不同位置的径向荷载与初始地应力情况下此处径向围岩压力的比值。

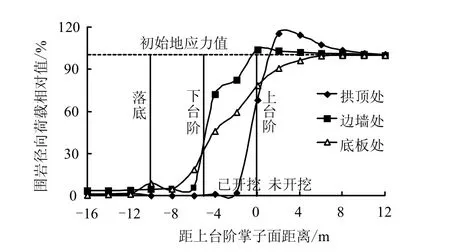
图4 台阶法施工隧道洞壁径向应力变化过程Fig.4 The load changing process of the wall rock during excavation

图中的3条竖线分别为上台阶、下台阶及落底时刻开挖到达的位置。通过相关文献的表述可知[1]，隧道围岩荷载主要来源于围岩压力，在分析过程中近似地认为，径向应力变化过程等同于围岩压力。

对于拱顶位置的径向荷载变化过程，根据数据曲线的变化趋势可以发现，拱顶位置的径向荷载主要受到上台阶开挖的影响，其整体上可以分为3个阶段；一是在开挖到监测点之前，拱顶处的径向荷载处于随着开挖临近荷载增加的阶段，在上台阶开挖面距离监测点大约2 m，即开挖之前一个循环进尺左右时，荷载增加的程度达到最大；二是在上台阶开挖通过监测点的前后各2 m，即一个循环进尺范围内，拱顶处的径向荷载发生急剧释放。分析认为，这是由于隧道拱顶位置的围岩受到上台阶开挖的扰动影响最大，上台阶的开挖使监测点位置的围岩下方瞬间出现临空面，原本作用于开挖掉那部分岩体的拱顶径向荷载失去荷载作用对象，故此处的岩体开始发生应力调整，由起初的竖向应力为主逐渐调整为水平向应力占主导。三是上台阶开挖面开挖穿过拱顶监测点一个循环进尺的距离之后，拱顶位置的径向应力在上台阶开挖穿过一个循环进尺之后基本不再发生变化。由图中曲线数据可知，上台阶长度确定为5 m是较为合理的，下台阶开挖时拱顶位置的荷载已基本释放完毕，有利于拱顶处围岩的稳定。

边墙位置的径向荷载与拱顶类似，在上台阶开挖到监测点所在断面时，边墙处的径向荷载发生了一定程度的增加，为初始地应力的 5%左右。上台阶开挖后边墙处的径向荷载开始释放，释放速率与拱顶处相比较缓慢，释放速率是同时刻拱顶的 1/3左右。边墙处径向荷载的主要释放过程处于下台阶开挖前后各一个循环进尺距离的范围内，在这两个循环的开挖过程中边墙处释放的荷载占释放荷载总数的78%。故通过调整下台阶开挖断面形式等手段可减弱下台阶开挖对边墙的影响，有利于优化边墙荷载释放，使荷载释放速率更为平缓。

隧道底板位置的径向荷载释放过程，受到了台阶法开挖全过程的影响。从受到开挖影响开始，底板位置的径向荷载一直处于不断减少的过程中，且荷载释放的速率比较平稳，每次开挖前后荷载释放过程均没有发生突变。此外，由于隧道底板位置不同于拱顶及边墙，即使围岩发生失稳破坏也不会对隧道的整体稳定性和结构安全造成太大的破坏，故隧道底板径向荷载的释放过程可以不作为研究分析的重点。

通过以上对台阶法开挖过程中隧道断面上不同位置的围岩荷载释放过程的分析研究，发现在台阶法开挖过程中，随着开挖的逼近，相同断面不同位置的荷载释放过程存在着一定的差异。受到上台阶首先开挖的影响，拱顶位置围岩首先开始荷载释放。并且在台阶法开挖逼近监测断面的过程中，拱顶及边墙位置的围岩在应力调整过程中首先发生荷载集中现象，且不同位置的荷载集中程度不同。

所以说，通过对台阶法开挖过程中的洞壁荷载释放过程分析，发现同一个断面上不同位置的荷载释放过程存在很大差异，这就需要对断面整体荷载状态进行综合研究。

5 断面整体荷载状态研究

在断面整体荷载释放状态的研究中，首先取上、下台阶开挖面位置的断面整体荷载状态进行单独分析。

图5为台阶法开挖过程中上台阶掌子面位置断面整体荷载状态，其中，黑色实线为隧道开挖轮廓，阴影部分的宽度表示洞壁该点的径向荷载与初始应力状态径向荷载比值的大小，黑色虚线为比值1的初始状态曲线。由图中曲线可知，上台阶开挖面上不同位置的荷载释放程度存在很大差异，即在应力调整的过程中，相同断面不同位置的荷载的释放是不同步的。上台阶的开挖主要对隧道上半断面的围岩的荷载释放造成影响。围岩径向荷载从拱顶到两侧边墙的集中程度逐渐增加，拱顶位置荷载释放最多，洞壁与上台阶开挖底面交界的位置的荷载集中程度达到最大，这两个位置的荷载集中程度最大，也就意味着在上台阶开挖后这两个位置围岩向隧道内发生变形和失稳的趋势最大，应对此处围岩加强支护及监控量测频率，以防此处岩体由于径向荷载变化过大发生剪切破坏。而此时隧道未开挖部分的荷载释放过程基本同步，且对已开挖临空部分的稳定基本没有影响。

图5 上台阶开挖面断面整体荷载状态Fig.5 Load condition of excavating section during upper bench cutting

图6为台阶法开挖过程中下台阶掌子面位置断面整体荷载状态，由图可知，在下台阶开挖过后不同位置的荷载释放情况存在较大差异，拱顶位置在上台阶开挖过后荷载进一步释放，当下台阶开挖到断面位置时已经趋近于全部释放，但下半部分边墙由于之前受到下台阶未开挖的钳制作用，还残存有较大的径向荷载，这同时也说明了在下台阶开挖过后隧道断面上径向荷载最大，即最容易发生失稳的位置为拱脚位置，在隧道开挖的过程中，下台阶开挖过后应及时对隧道拱脚处施加支护，消除或者缓解拱脚处的径向荷载集中程度，同时也说明在下台阶开挖过后应该及时施作锁脚锚杆以确保拱脚围岩的稳定的必要性。

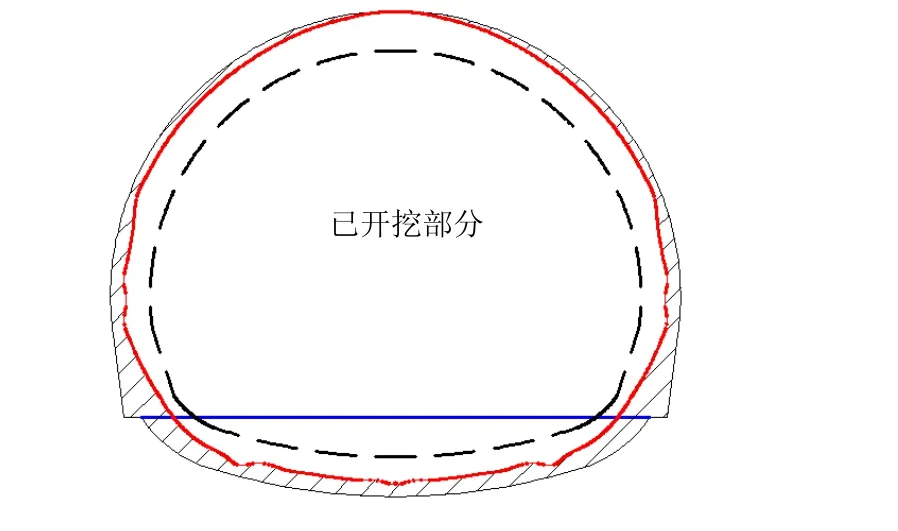
图6 下台阶开挖面断面整体荷载状态Fig.6 Load condition of excavating section during lower bench cutting

通过对上、下台阶开挖面的断面整体荷载释放状态进行分析，有必要引入新的概念，用以衡量断面的整体荷载释放状态。故定义断面综合荷载释放率和荷载释放差异系数概念如下：

（1）断面平均荷载释放率定义为开挖断面上所有径向荷载特征点荷载释放率曲线包络面积与初始地应力条件下的荷载释放率曲线包络面积的比值；

式中：Rt为断面平均荷载释放率；Si为第i个特征点的径向荷载释放率；n为洞壁围岩荷载释放率特征点总数；ha为洞壁围岩荷载释放率特征点平均间距。

（2）荷载释放差异系数定义为开挖断面上所有径向荷载特征点的径向荷载释放率与荷载释放率平均值之差的平方和除以荷载释放特征点总数得到的值。

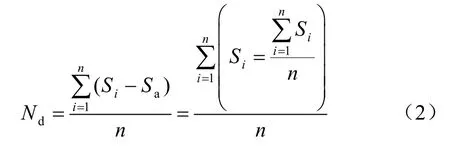
式中：Nd为荷载释放差异系数；Sa为断面上所有特征点的径向荷载释放率平均值。

通过断面综合荷载释放率和荷载释放差异系数的定义，可以通过其描述隧道施工过程中某断面整体的荷载释放状态，包括荷载释放平均程度及荷载释放进程的差异程度。

6 隧道施工过程模型试验

通过数值分析方法的研究，对施工过程的隧道断面整体荷载释放过程有了一定的认识，在此基础上，又进行了隧道开挖过程地质力学模型试验，监测隧道开挖过程中洞壁不同位置的围岩径向压力，进一步对隧道施工的荷载释放过程进行研究

本次模型试验主要针对隧道台阶法施工过程中的荷载变化过程进行研究，在开挖前应首先模拟初始地应力条件，故应采用先加载后开挖的模型试验设计方式。研究荷载释放过程要首先明确隧道荷载的来源，本试验中主要考虑岩土体压力对隧道结构的影响，故将围岩压力的变化过程作为主要监测对象。相似材料是模型试验能否贴近真实工程情况的重要一环，本次试验采用山东大学自主研制并且已经申请专利的铁晶砂相似材料作为试验用岩体相似材料[13]。根据现场的地质情况进行符合相似比的相似材料研制工作。

为了与数值模拟结论进行对比分析，模型试验采用台阶法开挖，以监测台阶法开挖中的荷载变化过程。图7为模型试验过程台阶法开挖方案示意图（试验相似比为1：50），图8为模型试验台阶法开挖过程正面观察情况。

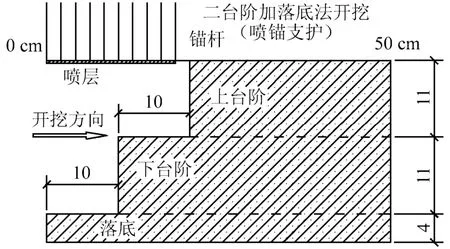
图7 台阶法开挖方案设计Fig.7 Method of the excavation in the model test

图8 模型试验台阶法开挖过程Fig.8 Excavation process of tunnel in model test

试验压力监测采用 DYB-1型微型土压力盒作为监测元件。其原理为微型单膜应变式土压力计，外形尺寸小、制作工艺成熟、测试范围宽、分辨率高、性能稳定、数据采集方便，是模型试验中测量压力的理想工具。

试验压力监测断面布置图9所示，其中，洞壁压力监测点的压力盒受压面均平行于隧道轮廓线的切线方向。

图9 压力监测断面布置Fig.9 Arrangement of stress monitoring section in model test

通过数值方法对隧道洞壁径向荷载释放过程的分析，发现同一个断面不同位置的荷载释放过程存在很大差异，故对于同一个断面不同位置的径向压力分布情况进行汇总分析。图10、11分别为上、下台阶掌子面开挖至监测断面位置时刻洞壁各个压力监测点数据图。

图10 上台阶掌子面位置洞壁径向围岩压力（单位：MPa）Fig.10 Pressures of wall rock during upper bench cutting (unit: MPa)

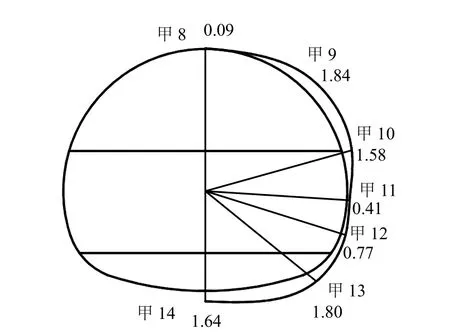
图11 下台阶掌子面位置洞壁径向围岩压力（单位：MPa）Fig.11 Pressures of wall rock during lower bench cutting (unit: MPa)

图10为上台阶掌子面位置的洞壁径向围岩压力分布图，通过上台阶对开挖面洞壁径向围岩压力分布情况的数据进行分析可知，上台阶开挖后拱顶到拱肩位置为整个断面上径向围岩压力最大的位置，而上台阶开挖范围以下直到隧道底板由于尚未受到开挖影响，径向压力值与初始状态下基本没有发生太大变化。

图11为下台阶掌子面位置的洞壁径向围岩压力分布图，通过分析可知，在下台阶开挖后断面的径向压力分布情况较之前有了较大的变化，边墙位置的围岩由于失去下台阶所开挖岩体的支撑作用，降低幅度较大。而拱肩位置相对其他位置仍分布有较大的径向围岩压力。

通过对试验数据进行分析可以发现，在隧道施工过程模型试验中，隧道洞壁围岩径向压力在掌子面推进的过程中发生了明显的变化，且不同位置的压力变化过程存在明显差异，荷载释放过程受开挖工法的影响较大，与之前进行的数值模拟得到的规律较为吻合。

7 结 论

（1）通过数值分析的方法对隧道台阶法开挖的荷载释放过程进行了深入研究，认识到同一个断面不同位置的荷载释放过程在隧道施工过程中并不是同步的，而且由于开挖工法的不同存在着很大的差异；

（2）定义了断面综合荷载释放率和荷载释放差异系数的概念，用以描述隧道施工过程中某断面整体的荷载释放状态，包括荷载释放平均程度及荷载释放进程的差异程度。通过这两个指标，可以简便地了解断面整体荷载的释放进程；

（3）通过开展隧道施工过程地质力学模拟试验，对数值分析中得出的结论加以验证，进一步证明了隧道施工过程中相同断面不同位置的荷载释放进程存在明显差异。同时也说明将断面整体作为荷载释放过程的研究对象是非常有必要的；

（4）现场监测是获取数据的重要手段，同时工程实际也是室内数值研究和试验研究的最终落脚点，通过分析监测数据对文中得到的结论进行进一步深入研究是非常有必要的，也能够对现有结论的正确性进行进一步验证，是下一步研究的方向和重点。

[1]关宝树. 隧道工程设计要点集[M]. 北京: 人民交通出版社, 2003.

[2]孙钧, 朱合华. 软弱围岩隧道施工性态的力学模拟与分析[J]. 岩土力学, 1994, 15(4): 20－32.SUN Jun, ZHU He-hua. Mechanical simulation and analysis of behaviour of soft and weak rocks in the construction of a tunnel[J]. Rock and Soil Mechanics,1994, 15(4): 20－32.

[3]朱维申, 何满潮. 复杂条件下围岩稳定性与岩体动态施工力学[M]. 北京: 科学出版社, 1996.

[4]朱维申, 李术才, 白世伟, 等. 施工过程力学原理的若干发展和工程实例分析[J]. 岩石力学与工程学报, 2003,22(10): 1586－1591.ZHU Wei-shen, LI Shu-cai, BAI Shi-wei, et al. Some developments of principles for construction process mechanics and some case studies[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 1586－1591.

[5]GU D S, DENG J, LI X B. Three-dimensional numerical simulation of excavation and backfilling in mining engineering[J]. Transactions of Nonferrous Metals Society of China, 1999, 9(2): 417－421.

[6]金丰年, 钱七虎. 隧洞开挖的三维有限元计算[J]. 岩石力学与工程学报, 1996, 15(3): 193－200.JIN Feng-nian, QIAN Qi-hu. Simulation of threedimensional tunnel excavations[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(3): 193－200.

[7]刘建华, 朱维申, 李术才. 小浪底水利枢纽地下厂房岩体流变与稳定性 FLAC3D数值分析[J]. 岩石力学与工程学报, 2005, 24(14): 2484－2489.LIU Jian-hua, ZHU Wei-shen, LI Shu-cai. Analysis of rheological characteristics and stability of surrounding rock masses of Xiaolangdi Hydrojunction underground caverns by using FLAC3D[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14): 2484－2489.

[8]SWOBODA G, ABU-KRISHA A. Three-dimensional numerical modeling for TBM tunnelling in consolidated clay[J]. Tunneling and Underground Space Technology, 1999, 14(3): 327－333.

[9]SHALABI F I. FE analysis of time-dependent behavior of tunneling in squeezing ground using two different creep models[J]. Tunneling and Underground Space Technology, 2005, 20(3): 271－279.

[10]刘涛, 沈明荣, 陶履彬, 等. 连拱隧道动态施工模型试验与三维数值仿真模拟研究[J]. 岩石力学与工程学报,2006, 25(9): 1802－1808.LIU Tao, SHEN Ming-rong, TAO Lü-bin, et al. Model test and 3D numerical simulation study on excavation of double-arch tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1802－1808.

[11]陈育民, 徐鼎平. FLAC/FLAC3D基础与工程实例[M].北京: 中国水利水电出版社, 2008.

[12]于学馥, 郑颖人, 刘怀恒, 等. 地下工程围岩稳定分析[M]. 北京: 煤炭工业出版社, 1983.

[13]张强勇, 王汉鹏, 李勇, 等. 铁晶砂胶结岩土相似材料及其制备方法: 中国, ZL2005101045814[P]. 2007-09-12.