不对称双连拱海底隧道施工引起的地层变形分析
2011-09-20张成平王梦恕
王 凯,张成平,王梦恕
(北京交通大学 隧道及地下工程教育部工程研究中心,北京 100044)
1 引 言
随着经济建设的高速发展,由于城市市区工程的增加、土地利用上的限制以及保护文物和环境等问题,城市建设中采用连拱隧道的情况不断增加。对于城市隧道,人们不仅关心隧道的结构安全,更加关注隧道施工对环境和生态的影响。城市隧道开挖使地层从原有的平衡状态向新的平衡状态转化,地层内部和地表较大范围内将产生位移和变形,这种现象对于浅埋大跨连拱隧道尤其敏感。为有效地预防和减少隧道施工引起的地表沉降和变形及其对周围环境所造成的损害,有必要研究隧道施工引起的地层变形规律并提出较为可靠的预计与控制方法[1-2]。目前,国内工程技术人员和相关学者对连拱隧道施工引起的地层变形进行了一些有意义的研究工作。何川等[3]对连拱隧道软弱围岩洞口段进行了施工全过程数值模拟,并用相似模拟试验进行验证和补充,提出了该类隧道施工全过程的地层位移规律和施工中应重点关注的区域。汪海滨等[4]结合城市浅埋大跨连拱隧道工程实例,根据现场监测数据进行反分析,采用数值模拟方法对开挖沉降曲线的偏态性及其内在机制进行了深入研究,并提出了具体防范对策。汪振伟等[5]以重庆彭家花园双连拱隧道为工程背景,就矿山法双连拱隧道施工引起的地表变形进行了研究。尽管对连拱隧道施工引起的地层变形的研究取得了一些很有应用价值的成果,但对于不对称双连拱隧道施工引起地层变形的研究还很少,而且城市隧道的地质荷载条件和周边环境比山岭隧道复杂得多,因此,对城市浅埋连拱隧道施工引起的地层变形开展研究工作很有必要。
青岛胶州湾海底隧道全长7 800 m,是连接青岛市主城与辅城的重要通道,南接薛家岛,北连团岛,下穿胶州湾湾口海域,其中海域段长3 950 m,由两条正线隧道、一条服务隧道、团岛端进出匝道隧道组成。青岛海底隧道主隧道与匝道交叉过渡段断面类型较多,隧道结构形式变换频繁,而且断面跨度大,施工工序多,受力状态复杂。其中 D11Z型大跨度不对称双联拱断面位于里程ZK2+800.78~ZK2+811.55,其开挖跨度为27.1 m,开挖高度为10.0 m,隧道最大覆盖层厚度14.78 m,围岩级别V级,是施工难度很大的地下洞室群。为比较准确地分析青岛海底隧道不对称双联拱断面施工对周围环境的沉降影响,本文分别采用隧道施工地层变形预测的经验公式和 FLAC3D软件计算青岛海底隧道不对称双联拱断面施工引起的横向地表沉降、地表以下不同埋深地层沉降、横向地表水平位移,通过相互验证和回归分析,得出不对称双连拱隧道施工地层运动的基本规律。
2 隧道施工地层变形预测的经验公式
隧道施工中影响地层变形的因素很多,地表移动和变形的大小主要受隧道的埋深、断面尺寸、地层条件、支护方式以及施工方法的影响。关于隧道施工引起的地层变形的研究方法主要包括经验法、随机介质法、解析法、离心模型试验法、数值分析法,其中Peck公式无疑是最简便、也是应用最为广泛的方法。
2.1 横断面地表沉降
在 Martos[6]首次提出隧道开挖引起的地表横向沉降槽符合高斯分布的基础上,Peck[7]、Schmidt[8]、O’Reilly和 New[9]等学者总结了当时广泛应用的经验方法,并提出了地表沉降横向分布的预测公式(即Peck公式):
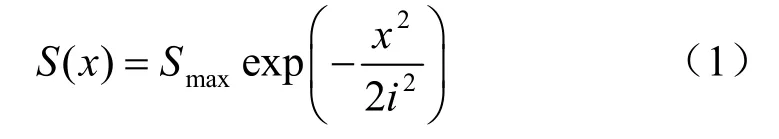
式中:S(x)为距离隧道中心轴线x处的地表沉降量;Smax为隧道中线处的地表最大沉降量;i为地表沉降槽的宽度系数,亦即沉降曲线反弯点至隧道中线的水平距离,它定义了沉降槽的形状与范围。
对式(1)进行积分可得到隧道掘进方向上单位距离的沉降槽体积,即地层损失:

地层损失率即单位距离内沉降槽体积占隧道开挖体积的百分比

式中:Vl为地层损失率;R为隧道等效半径。
地表沉降槽宽度系数i与隧道开挖深度、断面尺寸、地层条件和施工条件等密切相关。Peck及其他学者对参数i的取值进行了大量的研究,给出了不同地层及不同埋深条件下对应的地表沉降槽宽度系数i的经验公式,见表1。

表1 沉降槽宽度系数i的计算公式Table 1 Formulae of determination of settlement trough parameter i
2.2 地表以下不同埋深地层沉降
对于地表以下至隧道以上地层,地层损失的体积假设依然成立[12],就是说地层沉降沿深度在任一横断面呈正态分布,最大沉降位于隧道中心位置处,随着隧道埋深的不断增加,地表最大沉降值不断增大,沉降槽宽度不断减小。常用的计算地表以下不同埋深地层沉降分布的方法主要有 Mair[12]、Atkinson和Potts[10]提出的经验公式,见表2。

表2 不同埋深地层沉降的计算公式Table 2 Formulae of determination of subsurface settlement
2.3 横断面地表水平位移
对于隧道开挖引起地表水平移动的研究相对较少,O’Reilly、New[9]和 Attewell[11]建议对黏土中的隧道,可假定地层位移矢量指向隧道轴线,从而存在下面的关系式:

式中:Sx为横断面地表水平位移;Sz为横断面地表沉降;z0为隧道轴线埋深。
Mair等[12]则假定地层位移矢量指向(1 +0.175/0.325)倍隧道轴线埋深处点,则有
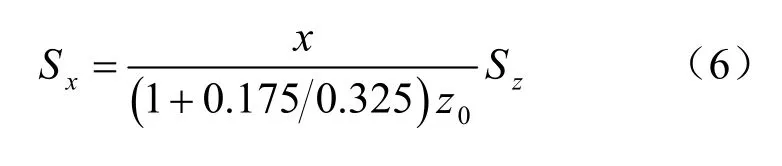
3 不对称双连拱隧道断面三维模拟
3.1 计算模型
整个 D11Z型不对称双联拱断面所在里程为ZK2+800.78~ZK2+811.55,选择位于其中的ZK2+800.78为典型断面。该断面围岩级别为V级,最大覆盖层厚度为 14.78 m。为进行三维动态施工情况的模拟以及考虑隧道开挖的端部效应,模型取纵向36 m进行模拟计算,隧道结构和关心部位附近采用小尺寸单元进行加密。整个计算范围为 200 m×100 m×36 m,模型网格划分见图1,图2为模型局部网格图,计算模型共有47 850个节点,44 016个单元。

图1 隧道计算模型Fig.1 Calculation model of tunnel

图2 局部网格模型Fig.2 Partial mesh model
3.2 计算参数
围岩物理力学参数沿隧道走向变化不大,故计算中采用断面 ZK2+800.78的围岩参数,按《青岛胶州湾湾口海底隧道工程地质详勘工程地质报告》选取,具体取值见表 3。围岩材料采用实体单元模拟,力学模型为Mohr-Coulomb塑性模型。
隧道初期支护采用钢拱架、挂网、C25喷射混凝土,二次衬砌采用C50钢筋混凝土,衬砌结构计算参数按照《公路隧道设计规范》[15]选取,见表4。初期支护和二次衬砌均采用实体单元模拟,力学模型为各向同性弹性体模型。钢拱架的作用采用等效方法予以考虑,即将钢拱架的弹性模量折算给混凝土[16],折算后的弹性模量可以按下式计算选取:
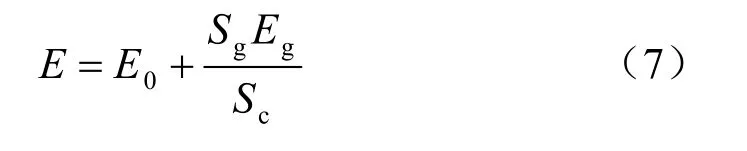
式中:E为折算后混凝土的弹性模量;E0为原混凝土的弹性模量;Eg为钢材的弹性模量;Sg为钢拱架截面积;Sc为混凝土截面积。

表3 围岩计算参数Table 3 Calculation parameters of surrounding rocks

表4 支护结构计算参数Table 4 Calculation parameters of supporting structures
3.3 初始应力场的获得
初始应力场的获得方法采取最典型的方法,对实体采取弹性模型,设定好边界条件,直接施加重力,使模型达到平衡。此时清空位移值,即获得了初始应力场。
3.4 施工步序
不对称双连拱隧道断面施工步序的描述如下:
(1)开挖中导洞并及时初支;(2)施作中隔墙模筑;(3)回填中导洞顶部及中隔墙左侧;(4)开挖匝道断面右导洞并及时初支;(5)匝道断面右导洞二次支护;(6)开挖匝道断面中部并及时初支;(7)匝道断面模筑封闭;(8)开挖主隧道断面左导洞上台阶并及时初支;(9)开挖主隧道断面左导洞下台阶并及时初支;(10)主隧道断面左导洞二次支护;(11)开挖主隧道断面中部并及时初支;(12)拆除临时支撑和中导洞左侧;(13)主隧道断面模筑封闭。
4 计算结果分析
4.1 地表沉降分析
图3是分别采用FLAC3D软件和各经验公式计算的地表沉降槽曲线。各经验公式计算参数中主隧道轴线埋深为20.77 m,等效半径为6.05 m,匝道轴线埋深为 21.31 m,等效半径为 4.76 m,均按ZK2+800.78典型断面几何尺寸换算得出。实测不对称双连拱断面施工完成时地表最大沉降值为30.56 mm,土体损失率Vl根据最大地表沉降反算得到。
从图中可以看出:
①不对称双连拱断面施工引起的地表沉降槽虽然呈现一定的不对称性,但基本仍呈正态分布,可近似为一单跨大断面施工引起的地表沉降槽曲线。

图3 地表沉降槽曲线Fig.3 Curves of surface settlement trough
②FLAC3D软件和各经验公式计算的地表沉降槽形态基本一致,其中采用Atkinson和Potts公式计算的沉降槽宽度最小,采用Lee等公式计算的沉降槽宽度最大。
③FLAC3D模拟的地表最大沉降值为26.97mm,比实测值偏小 11.7%,各经验公式的计算值与模拟值和实测值基本一致。
④FLAC3D模拟分析结果显示,距离隧道两侧一定区域内存在地表隆起的现象,这与大量工程实践相符合,但各经验公式无法模拟这一现象。
4.2 地表水平位移分析
图4是分别采用FLAC3D软件和各经验公式计算的地表水平移动槽曲线。

图4 地表水平移动槽曲线Fig.4 Curves of surface horizontal movement trough
从图中可以看出:
①不对称双连拱断面施工引起的地表水平移动槽基本呈中心对称分布,可近似为一单跨大断面施工引起的地表水平移动槽曲线。
②FLAC3D软件和各经验公式计算的地表水平移动槽形态基本一致,其中采用 Atkinson和 Potts公式和式(6)计算的水平移动槽宽度最小,采用FLAC3D软件计算的水平移动槽宽度最大。
③FLAC3D模拟分析结果显示,距离隧道两侧一定区域内地表存在远离隧道中心的现象,但各经验公式无法模拟这一现象。
4.3 地表以下不同埋深地层竖向位移分析
地表以下不同埋深地层竖向位移曲线如图 5~8所示。从图中可以看出:
①从拱顶到地表的地层沉降量逐渐减小,开挖的影响范围却逐渐增大。
②当地层埋深较浅时,FLAC3D模拟值和各经验公式所计算的结果差别不大。埋深2.5 m地层最大沉降 Mair公式计算值比模拟值偏大 8.4%,Atkinson 和Potts公式计算值比模拟值偏大13.4%;埋深 5 m地层最大沉降 Mair公式与 Atkinson和Potts公式计算值分别偏大15.8%和19.0%。而随着地层埋深的不断增加,FLAC3D模拟值和各经验公式所计算结果的差别不断增大。埋深10 m地层最大沉降两公式计算值比模拟值分别偏大 35.9%和34.5%;埋深14.78 m地层最大沉降两公式计算值分别偏大53.9%和51.6%。
③当地层埋深较浅时,地层沉降槽曲线的不对称性不明显,不对称双连拱断面产生的沉降槽可近似为一单跨大断面产生的沉降槽。随着地层埋深的不断增加,FLAC3D模拟反映的由于断面不对称引起的沉降槽的不对称性越来越明显,沉降曲线也越来越偏离正态分布。尤其是埋深10 m和14.78 m地层的沉降槽曲线,这种不对称性已非常明显。但各经验公式反映不出这种不对称性,可见随着地层埋深的增加,再将不对称双连拱断面产生的沉降槽近似为一单跨大断面产生的沉降槽已不准确。

图5 埋深2.5 m地层竖向位移曲线Fig.5 Curves of subsurface settlement trough at a depth of 2.5 m

图6 埋深5 m地层竖向位移曲线Fig.6 Curves of subsurface settlement trough at a depth of 5 m

图7 埋深10 m地层竖向位移曲线Fig.7 Curves of subsurface settlement trough at a depth of 10 m
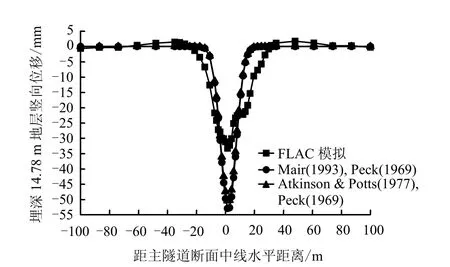
图8 埋深14.78 m地层竖向位移曲线Fig.8 Curves of subsurface settlement trough at a depth of 14.78 m
4.4 地表以下不同埋深地层水平位移分析
地表以下不同埋深地层水平位移曲线如图 9~12所示。从图中可以看出:
①不同埋深地层水平移动槽的宽度和峰值的变化规律与地层沉降槽的变化规律相似,不同的是水平移动槽的峰值位置随着地层埋深的增加而向隧道中心靠拢。
②当地层埋深较浅时,FLAC3D模拟值和表 2与式(6)联合计算的结果差别不大。埋深2.5 m地层最大水平位移Mair公式与式(6)的计算值比模拟值偏小9.9%,Atkinson 和Potts公式与式(6)的计算值比模拟值偏小5.7%;埋深5 m地层最大水平位移 Mair公式与式(6)的计算值比模拟值偏大20.3%,Atkinson 和 Potts公式与式(6)的计算值比模拟值偏大22.7%。而随着地层埋深的不断增加,FLAC3D模拟值和表2与式(6)联合计算的结果差别不断增大。埋深10 m地层最大水平位移各公式计算值比模拟值偏大均超过 50%。FLAC3D模拟值和表2与式(5)联合计算的结果差别更大。
③当地层埋深较浅时,地层水平位移曲线呈中心对称分布。随着地层埋深的不断增加,FLAC3D模拟的地层水平位移曲线越来越偏离中心对称分布,反映出一定的由于断面不对称引起的水平位移曲线的不对称性。尤其是埋深10 m和14.78 m地层的水平位移曲线,这种偏离性已非常明显。但各经验公式反映不出这种偏离性,可见随着地层埋深的增加,再按经验公式预测地层的水平位移已不准确。
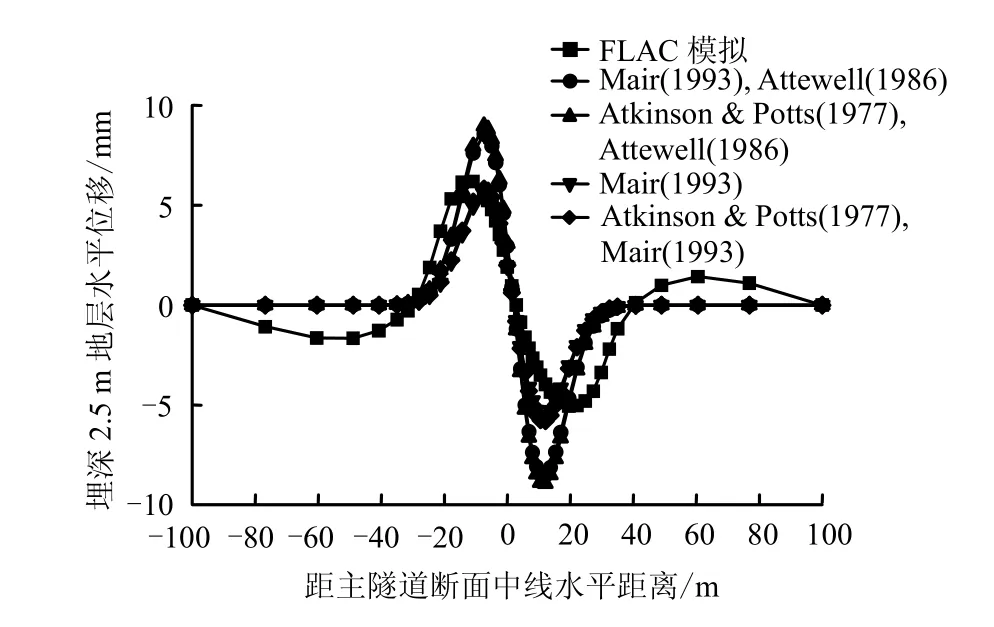
图9 埋深2.5 m地层水平位移曲线Fig.9 Curves of subsurface horizontal movement trough at a depth of 2.5 m

图10 埋深5 m地层水平位移曲线Fig.10 Curves of subsurface horizontal movement trough at a depth of 5 m

图11 埋深10 m地层水平位移曲线Fig.11 Curves of subsurface horizontal movement trough at a depth of 10 m

图12 埋深14.78 m地层水平位移曲线Fig.12 Curves of subsurface horizontal movement trough at a depth of 14.78 m
5 结 论
青岛海底隧道不对称双连拱断面施工引起的地层变形规律符合地层特性、隧道结构特点及浅埋暗挖法施工的实质。
(1)当地层埋深较浅时,不对称双连拱隧道断面地层沉降槽的不对称性并不明显,仍近似呈正态分布,可用各经验公式来预测。随着地层埋深的增大,地层沉降量不断增大,开挖的影响范围却逐渐减小。当地层埋深较大并接近拱顶时,不对称双连拱隧道断面地层沉降槽的不对称性已非常明显,此时用各经验公式来预测有较大偏差。
(2)当地层埋深较浅时,不对称双连拱隧道断面地层水平移动槽近似呈中心对称分布,与各经验公式计算结果的形态基本一致,位移值稍有差别。随着地层埋深的增大,地层水平移动槽的宽度逐渐减小。当地层埋深较大并接近拱顶时,不对称双连拱隧道断面地层水平移动槽的不对称性已非常明显,此时用各经验公式来预测有较大偏差。
(3)不同埋深地层沉降槽峰值位置基本固定,而水平移动槽两边的峰值位置随着地层埋深的增加而向隧道中心靠拢,表明对地面建筑物最危险的区域随着隧道埋深的变化在移动。
(4)经验公式只能对单一地层、单一隧道的地层变形进行初步估算,这些公式在理论上都存在明显的局限性,如无法考虑实际的应力场对变形的影响、无法考虑土的变形特性、强度特性等。因此,各经验公式无法模拟地表沉降槽距离隧道两侧一定区域内地表隆起的现象,以及地层水平移动槽距离隧道两侧一定区域内地表远离隧道中心的现象。而FLAC3D应用混合单元离散模型,采用全动态分析方法获取模型运动方程的时间步长解,可以准确模拟岩土材料的力学特性,追踪介质动态演化的全过程,深入探讨其时间效应与空间效应。因此,在预测复杂地质条件下不规则隧道断面开挖引起的地层变形时,FLAC3D较各经验公式有明显的优势。
[1]王梦恕, 刘招伟, 张建华. 北京地铁浅埋暗挖法施工[J].岩石力学与工程学报, 1989, 8(1): 52-61.WANG Meng-shu, LIU Zhao-wei, ZHANG Jian-hua. The boring excavation method and construction in Beijing metro[J]. Chinese Journal of Rock Mechanics and Engineering, 1989, 8(1): 52-61.
[2]阳军生, 刘宝琛. 城市隧道施工引起的地表移动及变形[M]. 北京: 中国铁道出版社, 2002.
[3]何川, 李永林, 林刚, 等. 连拱隧道施工引起的地层位移分析[J]. 岩土力学, 2005, 26(4): 612-616.HE Chuan, LI Yong-lin, LIN Gang, et al. Analysis of stratum displacement by multiple arch tunnel construction[J]. Rock and Soil Mechanics, 2005, 26(4):612-616.
[4]汪海滨, 李小春, 高波, 等. 城市浅埋大跨连拱隧道非对称开挖地表沉降偏态性研究及其对策[J]. 岩石力学与工程学报, 2008, 27(1): 3203-3209.WANG Hai-bin, LI Xiao-chun, GAO Bo, et al. Skewness distribution and countermeasure of ground settlement due to asymmetrical excavation in urban shallow large-span double-arch tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 3203-3209.
[5]汪振伟, 付钢. 城市连拱隧道施工地表沉降分析及预测研究[J]. 岩土力学, 2009, 30(2): 418-421.WANG Zhen-wei, FU Gang. Analysis and prediction of surface subsidence of double-arch tunnel construction in city[J]. Rock and Soil Mechanics, 2009, 30(2): 418-421.
[6]MARTOS F. Concerning an approximate equation of subsidence trough and its time factors[C]//Proceedings of the International Strata Control Congress. Leipzig: [s. n.],1958: 191-205.
[7]PECK R B. Deep excavation and tunneling in soft ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico city: [s. n.], 1969: 225-290.
[8]CLOUGH G W, SCHMIDT B. Design and performance of excavations and tunnels in soft clay[C]//Proceedings of Soft Clay Engineering. Elsevier: [s. n.], 1981: 569-634.
[9]O’REILLY M P, NEW B M. Settlements above tunnels in the United Kingdom—Their magnitudes and prediction[C]//Proceedings of Tunnelling 82. London:Institution of Mining and Metallurgy, 1982: 173-181.
[10]ATKINSON J H, POTTS D M. Subsidence above shallow tunnels[J]. Journal of Geotechnical Engineering, ASCE,1977, 103(4): 307-325.
[11]ATTEWELL P B, YEATES J, SELBY A R. Soil movements induced by tunneling and their effects on pipelines and structures[M]. London: Blackie and Son,1986: 78-85.
[12]MAIR R J, TAYLOR R N, BRACEGIRDLE A.Subsurface settlement profiles above tunnels in clays[J].Geotechnique, 1993, 43(2): 315-320.
[13]LOGANATHAN N, POULOS H G. Analytical prediction for tunneling-induced ground movements in clays[J].Journal of Geotechnical and Geoenvironmental Engineering, 1998, (9): 845-856.
[14]LEE C J, WU B R, CHIOU S Y. Soil movements around a tunnel in soft soils[C]//Proceedings of the National Science Council, Part A: Physical Science and Engineering. [S. l]: [s. n.], 1999.
[15]重庆交通科研设计院. JTG D70-2004 公路隧道设计规范[S]. 北京: 人民交通出版社, 2004.
[16]李术才, 朱维申, 陈卫忠, 等. 弹塑性大位移有限元方法在软岩隧道变形预估系统研究中的应用[J]. 岩石力学与工程学报, 2002, 21(4): 267-271.LI Shu-cai, ZHU Wei-shen, CHEN Wei-zhong, et a1.Application of elasto-plastic large displacement finite element method to the study of deformation prediction of soft rock tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 267-271.
