互补算法在一维非线性固结求解中的应用

邓岳保，谢康和

（浙江大学 岩土工程研究所，杭州 310058）

1 引 言

由于二向、三向固结理论在指标测定与计算求解方面存在诸多困难，Terzaghi单向固结理论在工程中仍被广泛应用。该理论建立在一系列简化和假设基础之上，如假定土体是均质饱和的理想弹性材料、土层的压缩和水的渗流只沿着竖向发生、渗透系数和压缩系数是常数、大面积的外荷载瞬时施加等。这些假定是对实际情况的理想化，因而理论结果与实际情况常常存在差异。对此，国内外学者通过对Terzaghi理论基本假设进行修正，得到考虑多种影响因素的固结理论，如考虑固结性状的非线性、固结荷重随时间改变等。目前，这些研究仍在进一步深入[1－6]。

笔者尝试将互补算法引入到非线性固结问题研究中。互补算法即计算互补问题的方法，是数学规划的一个重要分支。研究者对其广泛关注始于 20世纪60年代中期。40多年来，互补问题己发展成为数学、经济、工程等多个学科非常受欢迎的工具。其在工程领域中的应用包括弹塑性力学问题、接触力学问题、断裂力学问题、润滑问题、最优控制问题及交通平衡问题等[7－10]。上述研究通过挖掘互补关系，可使得待求问题模型化为互补问题，从而最终归结为利用互补算方法求解互补问题。应用互补算法的优越性在于，一方面使得所求问题有自然、清晰的数学描述、另一方面可运用其丰富而实用的理论去分析和求解问题[10]。

下文以一维非线性固结为例进行推导。首先将固结土体的压缩特性曲线进行分段线性拟合，然后挖掘其中的互补条件，构造互补模型，并将其应用于固结微分方程的差分求解。最后，通过与迭代法解答和太沙基进行对比以验证该法的合理性。

2 互补条件构造

2.1 互补问题及算法

互补问题的数学描述是：给定函数F(x)，求矢量x，使满足如下的方程和不等式条件，

上式等价的分量形式表达为

式(1)中，当 F(x)是线性函数，即 F(x)=Mx+q（M为n阶矩阵，q为n阶向量）时，上述问题为线性互补问题，否则为非线性互补问题。互补问题的名称来自于式(1)中的第3个方程，称为互补条件，即互补对( xi， Fi(x))中至少有一个变量为0。

对互补问题的深入研究，促进了互补算法的发展。目前，计算互补问题的方法主要包括Lemke算法、方程组类算法和内点法等。有关这些算法的研究可参考文献[8, 10－11]。下面将在e-σ′关系拟合曲线中寻找互补条件并构造互补方程。

2.2 e-σ'关系曲线及互补条件

不论是太沙基的单向固结理论，还是目前规范中的沉降计算，均取压缩曲线上的压缩系数为常数，相当于用直线拟合e-σ′关系曲线。然而实际上，根据常规的侧限压缩试验或三轴试验，不同类型土(尤其是高压缩性土)的 e-σ′关系曲线均反映出非线性的特点。为此，本文用分段线性来进行逼近。出于简化推导过程，选择分段数为 2（该法可方便地推广到多分段数）。

压缩曲线分段拟合情况如图1（分为OA和AB两段所示），线性分段的分界点为A(eA，σA′)。拟合曲线可描述为

式中：av1、av2分别为OA段和AB段的压缩系数，由曲线形式可知 av1≥ av2。

图1 土体e-σ' 曲线及其拟合曲线Fig.1 Soil e-σ' curve and its fitting curve

若令，

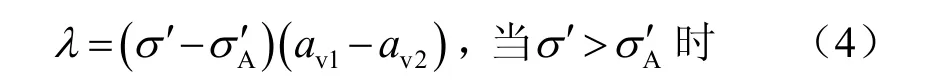
则有，

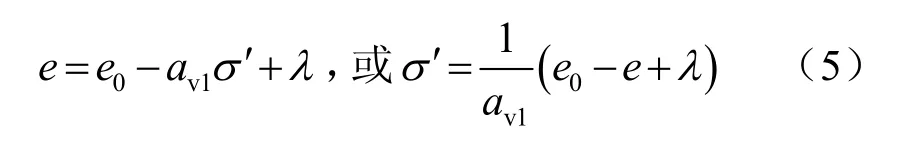
控制变量λ的物理意义如图1所示。当 σ′ ≤σA′时，λ=0，对应e-σ′关系曲线第1段；当 σ′＞ σA′ 时，λ＞ 0，对应e-σ′关系曲线第2段。至此，控制变量λ的引入，使得e-σ′关系曲线表达式统一于一个表达式。

将式(5)中σ′表达式代入式(4)并令左右相减得g，则：

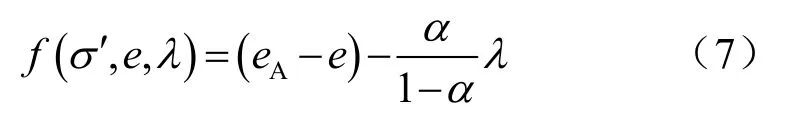
式中： α= av2av1。

结合式(4)、(6)和(7)分析 f和λ之间的关系：当σ′ ≤σA′ 时，λ=0，由 e-σ′曲线可知eA＜e，故f＜ 0；当 σ′＞ σA′ 时，λ＞0，由式(4)和式(7)的关系可得 f=0。

若引入v=-f，可得，

据前文分析有，

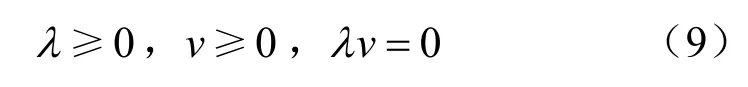
式(9)表明，v和λ之间为互补关系。这样，e-σ′关系曲线中的互补条件已经获得。

3 一维非线性固结求解

3.1 固结微分方程推导

在如图2所示厚度为H的均质饱和土层上施加无限宽广均布荷载 p，该荷载不随时间变化，土中附加应力沿深度均匀分布(即面积 abcd)，顶层面为排水边界，底层面为不透水边界。均质土层的初始孔隙比e0、渗透系数k不随时间变化。超孔隙水压力u、孔隙比e以及有效应力σ′均随时间变化而变化。分析中其他假设条件与太沙基假定相同，仅压缩系数为非常数。压缩系数在不同的应力阶段有不同的值，见式(3)。

图2 饱和软土一维固结分析Fig.2 One-dimensional consolidation analysis of saturated soil

考察土层顶面以下z深度的微元体dxdydz在dt时间内的变化。

（1）连续性条件

dt时间内微元体内水量Q的变化为

式中：q为单位时间内流过单位水平横截面的水量。dt时间内微元体内孔隙体积Vv的变化为

dt时间内微元体内水量的变化等于微元体内孔隙体积的变化，即则：

（2）达西定律

式中：i为水头梯度；h为超静水头；γw为水重度。结合式(12)和(13)，有：

（3）有效应力原理

根据有效应力原理有：

结合式(14)、(15)可得，

式（16）在推导过程中利用了一维固结过程中任一点竖向总应力σ不随时间变化的条件。

式(16)即为本文所要用到的一维非线性固结微分方程。该微分方程求解条件包括初始条件和边界条件。

初始条件：t =0时，e =e0，σ′ =0；

3.2 有限差分

式(16)形式上与太沙基一维固结微分方程相同，故可采用类似的有限差分法求解。地基差分计算网格划分如图3所示。图中地基深度方向分段数为m，时间分段数为n。时间和深度跨度分别为Δt和Δz，且Δz=H/m。

图3 差分计算网格Fig.3 Gridding of finite difference method

对式(16)进行有限差分，

式中：i =1,2,…, m，j =1, 2,…。处理后得，

相应地求解条件为

由式(18)可得：

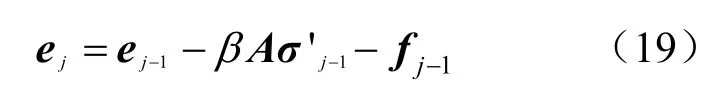
式(19)表明，在单向固结情况下，对于地基中的任意一点，只要知道该点及其上下节点处的孔隙比和有效应力（或超静水压力），就可以求得经过一个时段Δt后相同位置的孔隙比。根据太沙基单向理论假设，若e与σ′线性相关，则可由各节点处的初始孔隙比和初始有效应力，通过反复利用式(19)，逐点推算出后续任意时刻的孔隙比和有效应力（或超静水压力），获得解答。

然而，当e与σ′并非线性相关，而是在不同应力阶段有不同比例系数时，情况则发生变化。对照图4进行分析。当荷载施加后，地基中产生与外荷载相等的超静孔隙水压力，地基中有效应力为 0。随着时间推移，超孔隙水逐渐消散，有效应力逐渐增大。这一过程中，由于地基上层离排水面近，孔隙水消散迅速，有效应力增大快，孔隙比与有效应力关系率先进入e-σ′拟合曲线下一分段，而地基下层土体的孔隙比与有效应力关系还处于 e-σ′拟合曲线第一分段。这样，地基中存在一个界面，界面以上土体e-σ′曲线斜率为av2，界面以下土体e-σ′曲线斜率为av1。随着时间的推移和超静孔隙水的消散，该界面不断向下移动。

图4 不同时刻e-σ' 关系状态Fig.4 Correlation of e-σ' at different phases

上述分析表明，若e与σ′为非线性关系，则在反复利用式(19)时，需要反复判断e与σ′关系所处的阶段。下文利用e-σ′关系曲线的互补关系解决上述问题。

3.3 求解

根据式(8)，差分网格上的任意一点有，

结合式(19)和(20)得：

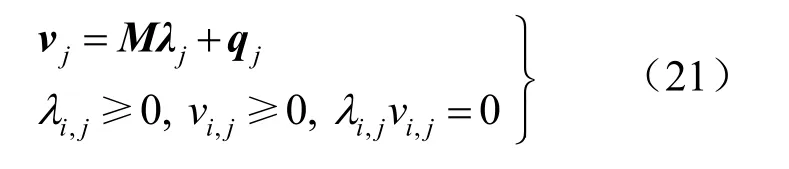
这样，当初始孔隙比和有效应力确定后，利用式(19)可获得下一时段的孔隙比，然后利用式(21)求解该时段的控制变量和有效应力，进而获得全部解答。下文称该法为互补模型法，其总的求解思路如下：

①给定参数 m、β，可确定Δz、Δt，完成网格划分；②由初始孔隙比e0和初始有效应力σ0′，根据式(19)确定经过Δt后的孔隙比e1；③将e1代入式(21)得q1，然后利用互补算法可确定Δt时刻的λ1，进而得到σ1′、u1；④根据Δt时刻计算结果和式(19)确定经过2Δt后的孔隙比e2，用上一步中相同的方法确定σ2′和u2。⑤依此类推，可得经过nΔt后的en、σn′和un。

求解过程中存在收敛性问题，具体计算时可通过改变β或调整Δt以达到收敛目的。

4 验 证

4.1 参数取值

计算过程中，参数取值情况如下：

地基参数：H =1 m，k =1.0 m/d，γw=10 kN/m3，e0=1.0，eA=0.8，av1=1.0，α=av2/av1=0.8；

网格划分：深度方向分段数 m=10，时间分段数n可取任意正整数。时间和深度跨度分别为Δt和Δz ，且Δz=H/m =0.1 m。

系数β=0.3，由此确定Δt。另外，仿效文献[12]，取荷载参数p =1，则可得相对于外荷载的无量纲超静孔隙水压力u。

4.2 与迭代法对比

用一般的迭代法与本文互补模型法进行对比。一般迭代法的计算步骤如下：

(1)确定初始量，包括初始孔隙比 e0、初始有效应力σ0′和初始超静孔隙水压力u0；(2)由式(18)确定经过Δt后的孔隙比 e1，再由式(2)运用判断语句确定有效应力σ1′，进而得到Δt时刻的超静孔隙水压力 u1；(3)根据Δt时刻计算结果和式(18)确定经过2Δt后的孔隙比e2，用上一步中相同的方法确定有效应力σ2′和超静孔隙水压力u2；(4)依此类推，可得经过nΔt后的孔隙比en、σn′和un。

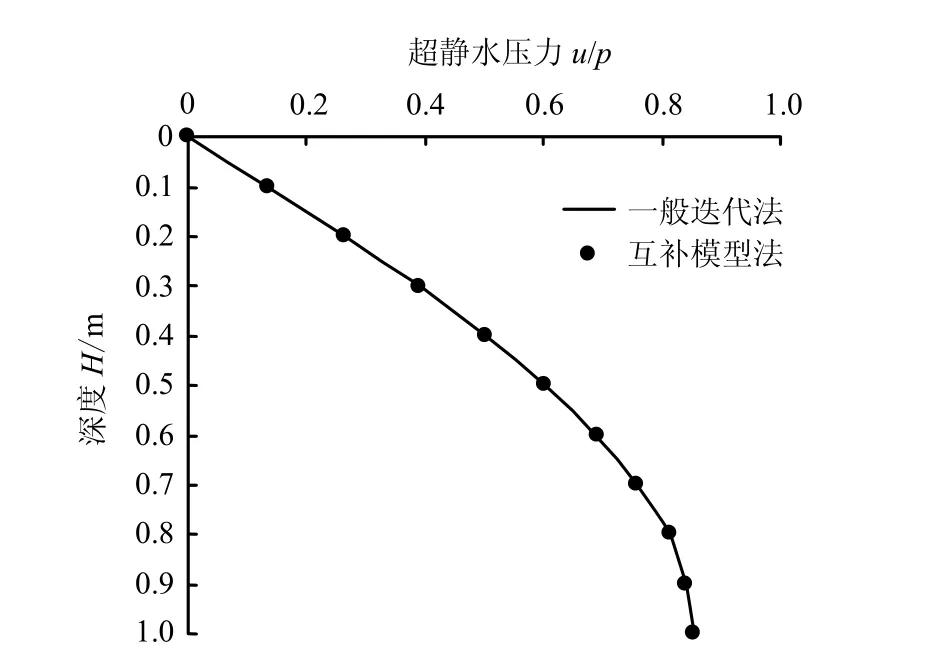
图5 超静孔隙水压力u对比结果Fig.5 Result contrast of u of two methods

对比计算结果发现，当两种方法的参数取值及网格划分均相同时，相同时刻的超静孔隙水压力结果完全一致。图5所示为时间段数n =50时两种方法得到的超孔隙水压力结果对比。

4.3 与太沙基理论对比

根据α的物理意义可知：当α=1时，分段线性压缩曲线变为一条直线。下文将这种特殊情况时的非线性计算结果与太沙基单向固结差分法计算结果（简称线性解）进行对比。

太沙基单向固结理论微分方程为

式中：av=av1= av2。求解条件如下，

初始条件：t =0时，u =u0；

太沙基单向固结理论差分解求解过程可参考文献[12]。对比该法和本文方法的计算结果发现：当参数取值及网格划分相同时，相同时刻的超静孔隙水压力结果亦完全一致。这样，两种验证结果均表明本文方法的合理性。

5 计算与分析

参数取值同上文验证部分。限于篇幅，下文仅给出超静孔隙水压力计算结果，并对其影响因素进行简要分析。最后对本文方法的优越性给予说明。

5.1 不同时刻线性解与非线性解对比

参数取值同上，不同时段线性解答与本文非线性计算得到超静孔隙水压力结果对比情况如图6。

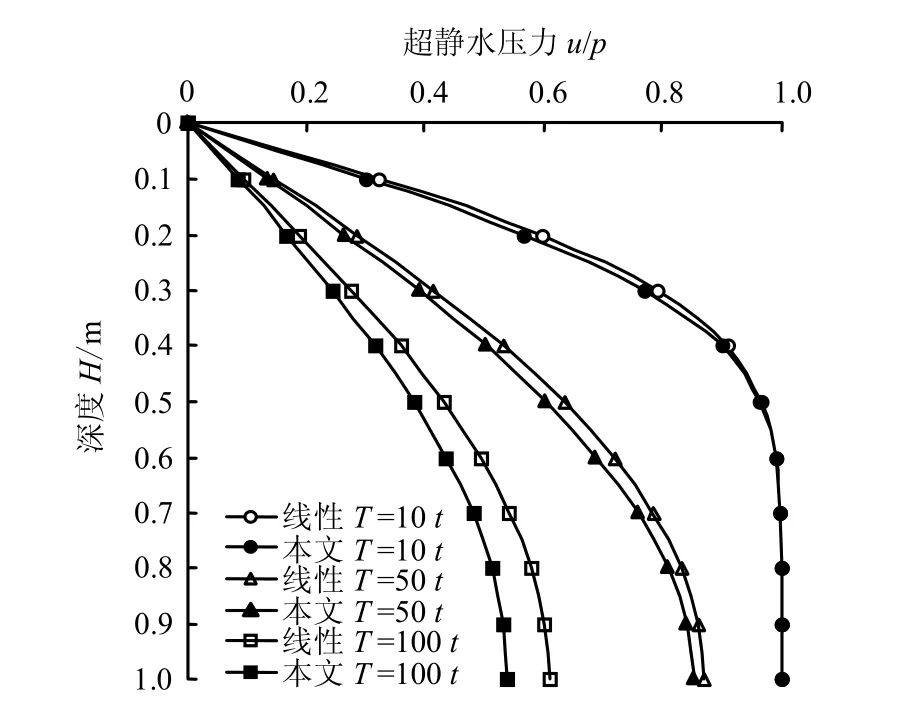
图6 不同时刻超静孔隙水压力u情况Fig.6 Solutions of u at different phases

由图6可知，由于考虑了压缩系数随有效应力增大而减小，非线性计算得到超静孔隙水压力消散快于线性计算结果，且随时间推移，两者相差越来越明显。

5.2 非线性计算影响因素分析

（1）非线性程度对本文计算结果的影响

参数α反映压缩曲线的非线性程度。改变α的取值，令其分别等于1.0、0.8和0.6。3种情况下，时间分段数n =50时，不同深度处超静孔隙水压力分布如图7所示。由图可知，随着非线性程度的增加，即压缩曲线上后一分段的压缩系数变小，孔隙水压力消散增快，固结速率加快。

图7 非线性程度对超静孔隙水压力u计算影响Fig.7 Effect of nonlinear level on the solution of u

（2）eA对计算结果的影响

参数 eA反映压缩曲线上进入下一线性段的门槛值。eA越接近初始孔隙比e0，表明越容易进入压缩曲线的下一分段。改变eA的取值，令其分别等于1.0、0.8和0.6。3种情况下，n =50时，不同深度处超静孔隙水压力分布如图8所示。由图可知，随着eA的减小，即进入压缩曲线后一分段的临界孔隙比变小，孔隙水压力消散减缓。

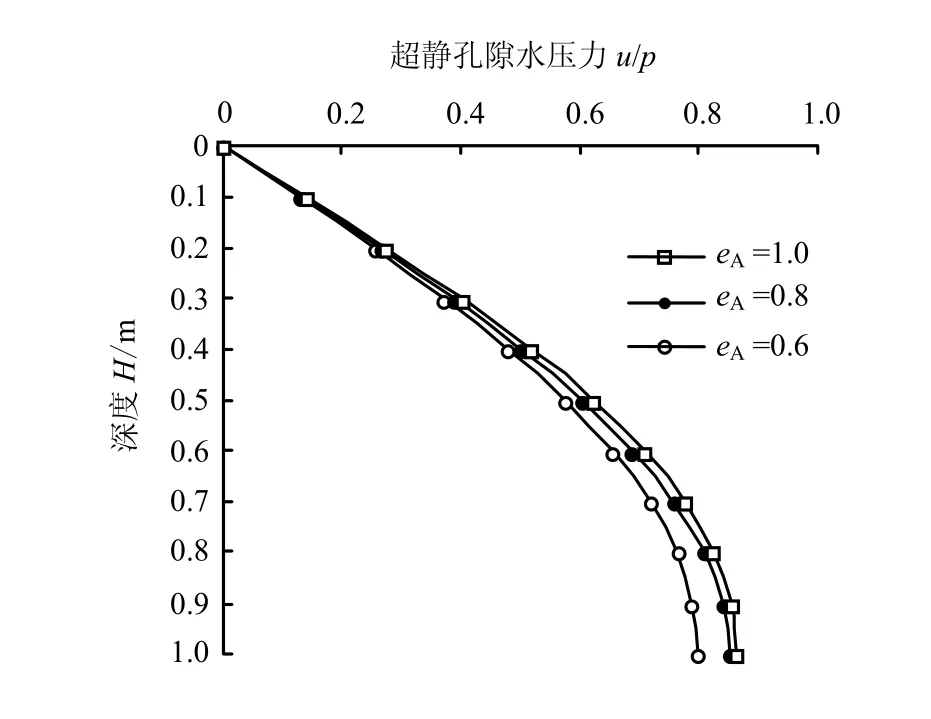
图8 eA对超孔隙水压力u计算影响Fig.8 Effect of eA on the solution of u

5.3 互补模型算法优越性说明

计算过程中发现，相比于普通迭代法，互补模型算法优越性有两点。

（1）计算效率

普通迭代法计算过程中，判断语句需要遍历不同时刻不同深度的各个节点，即运行mn次判断。互补模型法迭代次数则有所减小，对照图9进行说明。图9所示为本文方法得到的不同时刻不同深度控制变量λ解答。

图9 不同时刻不同深度控制变量λ 解答Fig.9 Solution of λ at different phases

由图可知：当T =10Δt时，计算程序只迭代了4次；当T =50Δt时，程序迭代了8次；随着时间的推移，迭代次数向m靠近。总和不同时刻迭代次数可知，互补模型算法程序总的迭代次数比mn小。这种减小幅度在网格划分密集时非常显著。

（2）控制变量求解的意义

控制变量λ解答一方面能反映迭代次数；另一方面还能反映不同时刻、不同深度地基土体所处的压缩状态。即：当λ=0为~时，地基土体处于压缩曲线的第1分段；λ=0时，则处于第2分段。仍对照图 9进行说明。由图可知：当 T =10Δt时，地基0.4 m以上土体压缩状态处于压缩曲线的第2分段，该部分土体进入非线性压缩状态；当T =50Δt时，地基0.8 m以上土体压缩状态处于压缩曲线的第2分段；而当T =100Δt时，地基土体全都处于压缩曲线的第2分段。

6 结 论

（1）互补模型算法与普通迭代法得到的结果一致，但在计算效率方面，由于互补模型算法是以最优收敛方向逼近真实解答，故其计算效率高，当其应用于复杂问题求解时在速度上具有优势。

（2）在线性计算程序中嵌入互补模型算法即可进行非线性分析，程序容易实现。

（3）互补模型算法中通过对控制变量的求解，可判断地基土体所处的压缩状况。

[1]XIE K H, QI T, DONG Y Q. Nonlinear analytical solution for one-dimensional consolidation of soft soil under cyclic loading[J]. Journal of Zhejiang University:Science A, 2005, 7(8): 1358－1364.

[2]问延煦, 施建勇. Terzaghi一维固结理论研究综述[J].西部探矿工程, 2003, (2): 1－4 WEN Yan-xu, SHI Jian-yong. Current research of Terzaghi one-dimensional consolidation theory[J]. West China Exploration Engineering, 2003, (2): 1－4.

[3]HSU T W, LU S C. Behaviour of one-dimensional consolidation under time-dependent loading[J]. Journal of Engineering Mechanics, ASCE, 2006, 132(4): 457－462.

[4]常林越, 王金昌, 朱向荣. 多级线性荷载下饱和软黏土一维大应变固结解析解[J]. 岩土力学, 2009, 30(8):2343－2347.CHANG Lin-yue, WANG Jin-chang, ZHU Xiang-rong.An analytical solution of 1-D finite strain consolidation of saturated soft clay under multistep linear loading[J]. Rock and Soil Mechanics, 2009, 30(8): 2343－2347.

[5]梁仕华, 齐添, 谢康和, 等. 超固结土的一维固结理论及其试验研究[J]. 应用力学学报, 2009, 26(2): 268－274.LIANG Shi-hua, QI Tian, XIE Kang-he, et al.Experimental verification of one-dimensional linear over-consolidation theory[J]. Chinese Journal of Applied Mechanics, 2009, 26 (2): 268－274.

[6]鄂建, 陈刚, 孙爱荣. 考虑低速非Darcy渗流的饱和黏性土一维固结分析[J]. 岩土工程学报, 2009, 31(7):1114－1118.E Jian, CHEN Gang, SUN Ai-rong. One-dimensional consolidation of saturated cohesive soil considering non-Darcy flows[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7): 1114－1118.

[7]LEMKE C E, HOWSON J T. Equilibrium points of bimatrix games[J]. Journal of the Society for Industrial and Applied Mathematics, 1964, 12: 413－423.

[8]FERRIS M C, PANG J S. Engineering and economic applications of complementarity problems[J]. SIAM Review, 1997, 39(4): 669－713.

[9]郭小明. 弹塑性接触问题的研究及其应用[D]. 南京:东南大学, 2002.

[10]何素艳. 互补问题算法研究及其在力学中的应用[D].大连: 大连理工大学, 2003.

[11]陈宝林. 最优化理论与方法(第二版)[M]. 北京: 清华大学出版社, 2005.

[12]李广信. 高等土力学[M]. 北京: 清华大学出版社,2004.