应用于数字锁相环的NCO设计

保 玲，佘世刚，周 毅，金玉琳

（兰州空间技术物理研究所 甘肃 兰州 730000）

数字锁相环已在数字通信、无线电电子学及电力系统自动化等领域得到广泛应用。数字锁相环用于信号解调时，对信号频率的准确度和稳定度要求比较严格，在数字锁相环设计中，NCO自动跟踪捕捉输入信号的频率，直至锁相环进入锁定状态，保持频率不再变化。NCO的设计采用DDS技术。DDS是近些年迅速发展起来的一种频率合成技术，具有频率分辨率高、频率转换速度快、相位噪声低、频率稳定度高以及能够灵活产生多种信号等突出优点。然而在实际中，NCO的数字化处理不可能是完全理想的，杂散的产生也不可避免，因此在电路设计中，应尽量减小杂散噪声，获得较为理想的输出。基于FPGA设计NCO，支持系统现场修改和调试，可大大缩短设计周期。

1 NCO工作原理

NCO主要由相位累加器、波形存储器（ROM）、数模转换器（DAC）和低通滤波器（LPF）构成，核心为数字部分，即相位累加器与波形存储器。NCO工作原理为：参考时钟fc每触发一次，相位累加器将对频率控制字进行线性相位累加，得到的相位码对波形存储器寻址，使之输出相应的幅度码，完成相位到幅值转换。该编码值存储于波形存储器中，存储器的字节数决定了相位量化误差。如需输出模拟波形，需送入DAC进行数模转换，最后经低通滤波器进行平滑处理，输出信号fo[1]。NCO结构如图1所示。

图1 NCO结构Fig.1 Structure of NCO

2 NCO设计与FPGA实现

相位累加器是整个NCO系统运转的关键，主要完成相位累加，实现输出波形频率可调功能，利用Verilog HDL实现相位累加器的模块设计，采用流水线编码方式来减小资源消耗。通过输入频率控制字就可以输出所需要频率的波形，累加器的位数N设置为16位，频率控制字位数KF为16位。

实验用主芯片为CycloneⅢ 系列EP3C40F484C6N。板上时钟频率fc为50 MHz，NCO输出频率fo为6.5 MHz，计算出

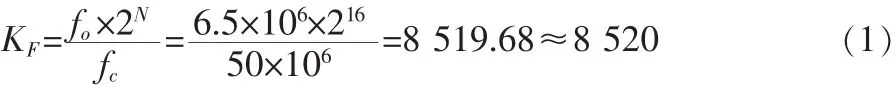
将频率控制字换算为二进制数，则KF=0010 0001 0100 1000。

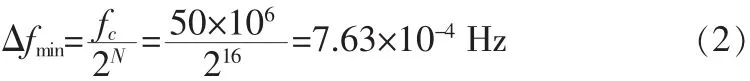
DDS的频率分辨率为频率控制字KF为[2]：

课题使用16 bit的相位累加器，如果全部用来寻址，则需要216bit存储空间。当相位精度要求较高时，所消耗的ROM资源量很大，因此采用ROM压缩技术，利用正弦函数的1/4对称性，只需存储未压缩前的1/4。波形存储器的设计基于ROM宏模块lmp_rom，设置ROM的宽度为10位，调用时产生数据文件.mif，然后直接在定制lmp_rom时，添加数据文件即可。

将设计好的NCO程序在Quartus II 9.0中编译综合并仿真，仿真波形如图2所示。

图2 NCO仿真波形Fig.2 Simulation of NCO

3 NCO杂散分析

NCO杂散来源主要有3个方面的因素：片内ROM容量有限引入的相位截断误差；幅度量化引入的幅度量化误差；DAC的非理想特性引入的DAC转换误差。由于杂散谱线可能非常靠近主信号，不能被滤波器有效地抑制。因此，对NCO杂散性能的分析和计算是NCO系统设计和应用中的重要问题。

1）相位截断误差：实际NCO为了达到一定的频率分辨率，通常相位累加器的位数N都取得大，如取N=24，32，48等。但受ROM体积、成本和功耗的限制ROM的容量远远小于2N，因此寻址ROM只采用相位累加器输出的高M位（M=N－B），其低B位被截断而未用，这样就引入了相位截断误差[3]。

理想NCO输出频谱为[4]：

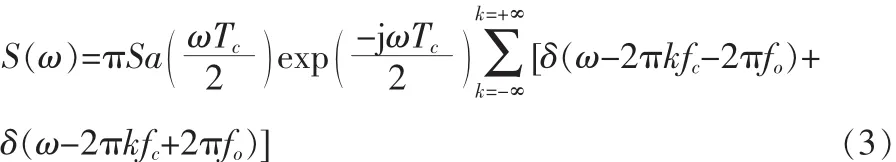
根据上式，理想NCO输出频谱分布在f=kfc±fo处，谱线幅度的包络具有Sa（x）函数的形状，有用频率fo=Kfc/2N对应的幅度为 πSa（πfo/fc）。

存在相位截断时NCO的无杂散动态范围SFDR为：

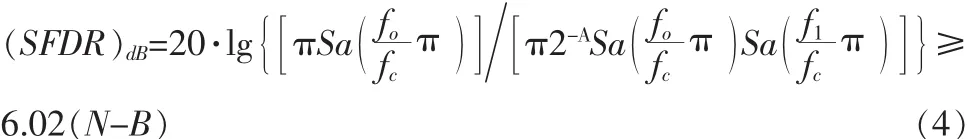
式中，f1为区间内幅度最大谱线对应频率，其值为

由式（4）可见，由相位累加器截断引起的信噪比取决于相位累加器截断位数，即与对ROM寻址的位数成正比，ROM的地址位越多（即存储量越大），其输出信号的信噪比也就越高。相位截断引入的最强杂散的相对主谱的电平由（N－B）决定。课题设计中ROM输出为10位，则ROM中有210个地址，因此有10个地址线，寻址位数也为10位，即（N－B）为10，则由相位截断引起的无杂散动态范围大于60.2 dB。

2）幅度量化误差：理论上，一个正弦样点幅值须用一个无限长的二进制代码才能精确表示，但实际NCO考虑到ROM的存储量、功耗以及DAC的分辨率等因素，ROM中只存储了无限长二进制码字的最高W位作为ROM的输出，也就引入了幅度量化误差。

ROM截断引起的幅度量化误差在NCO输出频谱上表现为背景噪声，所以对ROM截断的频谱分析又称之为NCO的背景杂散分析。由于NCO内部波形存储器中存储的正弦幅度值是用二进制表示的，对于超过存储器字长的正弦幅度值必须进行量化处理，这样就引入了量化误差。实际中ROM幅度量化多采用舍入量化方式[5]。

幅度量化的信噪比为

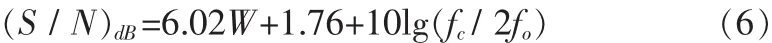
由于模数转换器DAC900为10位，因此ROM输出也取为10位，即W取值为10，故幅度量化的信噪比大于62 dB。

利用傅里叶级数，求出此量化误差信号经理想D/A转换后的频谱为

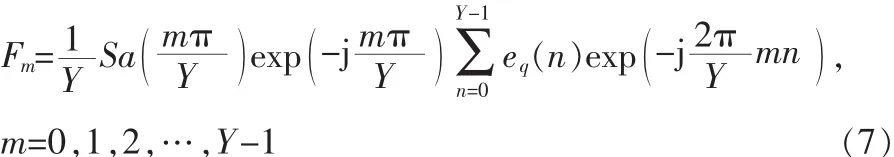
3）DAC非线性误差：实际的DAC只有有限位输入（即分辨有限），通常 D=8，10，12，14 等，另外 DAC 存在着比较严重的非线性特性（包括积分非线性，微分非线性，DAC转换过程中存在尖峰电流以及转换速度有限等），以及DAC转换过程中会出现尖峰脉冲等，所有这些都将导致NCO的输出大量的杂散信号。

DAC的非线性特性相当复杂，并且每个DAC的非线性特性也不尽相同，其数学模型难以建立，因此只对其做简单的定性分析。目前对于DAC所产生的杂散还不能给出定量的关系，只能对DAC引入的杂散给出估算公式[6]：

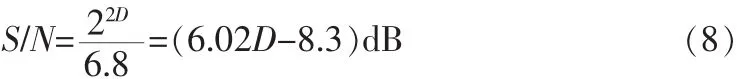
式中，D表示模数转换器的位数。课题选用DAC900，转换位数为10位，因此可算得DAC引入杂散信噪比约为51.9 dB。

4 下载调试与结果分析

通过FPGA开发软件Quartus II 9.0，将编译后的NCO设计文件在线编程到FPGA开发板上，从FPGA设定的输出端输出的仍为数字信号，外接数模转换器DAC900，将数字信号转变成输出频率受输入数字控制的正弦波信号。

将输出信号接至频谱仪，带宽调至95.17 kHz，分辨率带宽（Res BW）为 220 Hz，视频带宽（VBW）为 220 Hz[7]。 如图 3 所示。

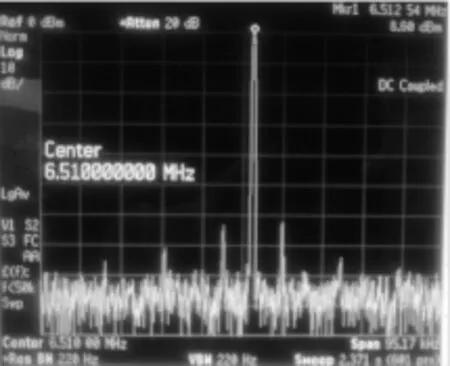
图3 NCO输出频谱Fig.3 Output spectrum of NCO

可测得杂散噪声如表1所示：

表1 杂散噪声分布Tab.1 Distributions of Spurious

带宽范围调至50 MHz，宽频带输出频谱如图4所示。

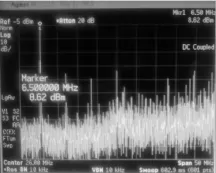
图4 NCO输出频谱Fig.4 Output Spectrum of NCO

分辨率带宽（Res BW）为10 kHz，视频带宽（VBW）为 10 kHz，信号功率为8.62 dBm。二次谐波为-49.05 dB；三次谐波为-53.06 dB。

为减小杂散噪声，采用低通滤波器滤除杂散噪声，设计一个七阶Butterworth型低通滤波器，在ADS中设计并仿真，其原理图如图5所示。

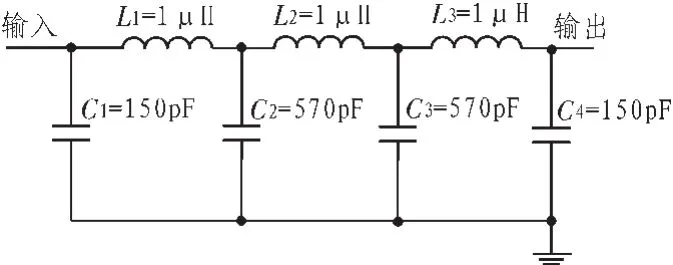
图5 LPF原理图Fig.5 Principle of LPF

经LPF滤波，在频谱仪上观察NCO输出，如图6所示。

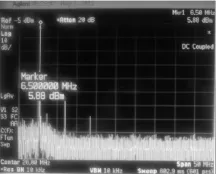
图6 滤波器输出频谱Fig.6 Output spectrum of filter

观察图6可知，加入LPF后，信号功率为5.88 dBm，二次谐波为-65.51 dB，衰减了16.46 dB；三次谐波为-79.18 dB，衰减了26.13 dB。

5 结束语

本文对NCO的工作原理和噪声来源作了介绍，基于FPGA设计出应用于数字锁相环的NCO，对三种杂散进行详细分析并提出抑制方法，最后对调试结果进行分析。实验证明，基于FPGA实现的NCO指标满足工程要求，应用于数字锁相环时，性能基本能满足大多数系统的使用要求，修改灵活，可根据需要进行接口和控制方式的修改，使得测试工作更加全面高效，从而提高调试效率。还具有DDS的优点，因此可在数字通信领域得到广泛应用。

[1]田耘，徐文波，张廷伟，等.无线通信FPGA设计[M].北京：电子工业出版社，2008.

[2]张安安，杜勇，韩方景.全数字Costas环在FPGA上的设计与实现[J].电子工程师，2006，32（1）：18-21.

ZHANG An-an， DU Yong， HAN Fang-jing.Design of implementation ofcostas loop on FPGA platform[J].Electronic Engineer，2006，32（1）:18-21.

[3]李海松，张奇荣，权海洋.DDS的相位截断及相应的杂散信号分析[J].微电子学与计算机，2006，23（2）：141-143.

LI Hai-song， ZHANG Qi-rong， QUAN Hai-yang.Analysis of spurious in DDS due to the phase truncation[J].Microelectronics and Computer，2006，23（2）：141-143.

[4]胡仕兵，汪学刚，姒强.直接数字频率合成技术杂散信号频谱性能分析[J].电路与系统学报，2009，14（5）:87-91.

HU Shi-bin， WANG Xue-gang， SI Qiang.Analysis of the spurious spectrums in direct digital frequency synthesizers[J].Journalof Circuits and Systems， 2009，14（5）:87-91.

[5]白居宪.直接数字频率合成[M].西安：西安交通大学出版社，2007.

[6]刘金亮.直接数字频率合成技术实现研究[D].北京：北京交通大学，2008:11-15.

[7]GIFFARD R P，CUTLER LS.A low-frequencyhigh resolution digital synthesizer [J]. Frequency Control Symposium，IEEE 1992:188-192.