基于幅值等分的数字化正弦信号生成的设计

李艳芳，陈增禄，毛惠丰

（1.西安工业大学北方信息工程学院 陕西 西安 710025；2.西安工程大学 陕西 西安 710048）

近年来，随着逆变器在各行各业应用的日益广泛，采用正弦脉宽调制（SPWM）技术控制逆变器提高整个系统的控制效果是人们不断探索的问题。逆变器的控制精度由基波和载波精度共同决定，而逆变器的开关频率又不断要求提高。在一些特殊的应用领域，所期望的SPWM逆变器的开关频率，调制精度以及调制波频率不断提高，使得即便是使用数字信号处理器[1-2]也很难同时满足速度和精度的要求。在大功率宽频带低失真逆变器的设计中[3-6]。

目前，正弦调制信号可以分为两种方法生成：一种方法是对模拟正弦信号实时采样并AD转换，另一种是实时数字合成方法[8-9]。文献[5]中采用模数转换器采样生成数字化正弦调制信号。文献[6]阐述了生成数字化正弦信号的新方法，文中给出线性差值和查表相结合的原理产生数字化正弦信号。

本文提出了一种基于幅值等分的数字化正弦调制信号生成的方法。该方法将正弦信号的幅值进行等分，实现了充分利用DAC的转换精度，实时生成正弦调制信号，并且应用硬件描述语言对系统进行了FPGA模块化设计。

文中首先阐述了数字化正弦调制信号生成的基本原理，对其进行误差分析，给出了这种方法的最大误差，证明了这种方法误差非常小。然后给出FPGA模块化设计，最后给出实验结果，证明了该方法是实用可行的。

1 生成的原理及FPGA模块化设计

1.1 基本原理

设标幺化的正弦信号对应的表达式为：

其中，ω为正弦信号的角频率，ω=2πfs，fs为正弦波频率。

对正弦调制信号幅值1进行N等份，即每个相邻幅值间隔距离是相等的。二进制中表示为N=2n-1-1，此处的N也同时为DAC转换最高精度，n最高位为符号位。那么，各个等分的幅值点的模拟量依次为 V1，V2，V3，…，Vk，Vk+1…V2n-1，其对应的数字量为 Vd1，Vd2，Vd3，…，Vdk，Vd（k+1）…Vd（2n-1），各等分幅值点对应的正弦调制信号的时间点依次为 t1，t2，t3，…，tk，tk+1…t2n-1。其原理图如图1所示。

二进制量化单位为q，即每个相邻阶梯间的幅值相差对应的数字量为“1”。 从图中我们可以看到，这种方法的基本原理是对幅值上进行等分，确定每个幅值等分点所对应的时间点，以前一个时间点为基准对输出的二进制幅值进行累加（减），实现数字化正弦波的生成。

由正弦量的表达方程可以得出：

则有，

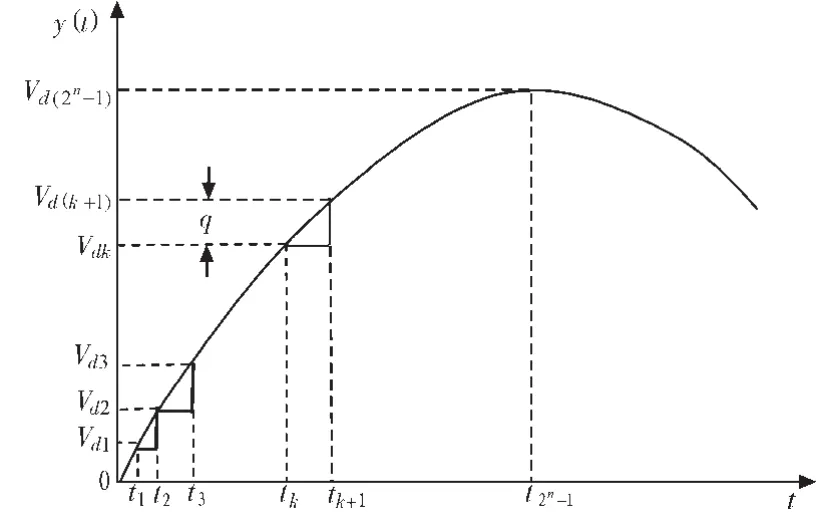
图1 数字化正弦信号生成的原理图Fig.1 The principle of digitized sin wave

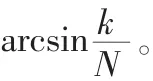
按照上面所述的原理，计算出每个等分点的幅值Vdk和其对应的时间点tk，进而计算出相邻两个等分点的时间差△t。相邻等分点之间的差值△V为数字量1。那么，只要每隔△t时间后令当前的数字量累加“1”即可实现数字化正弦信号生成。如需改变正弦信号的频率，只需在每个时间点基础上做处理即可，即

其中，Ts为期望正弦信号的周期，tk′为处理后tk对应的时间值。如需改变正弦信号的幅值，也只要使正弦信号乘以相应的数值即可。

1.2 FPGA模块化设计

图2为基于FPGA的数字化正弦调制信号生成原理图。设FPGA系统时钟频率为f0。A模块中存放数字化正弦调制信号 N 等分点对应的时间值 t1，t2，t3，…，tk，tk+1…t2n-1；B 模块为查找A模块中时间表时的地址计数器；C模块在任意系统时钟下，计算需要频率为fS正弦调制信号的实际时间点；D模块为tk间隔定时器；E模块为累加器；F模块为幅值处理。

图2 基于FPGA的正弦调制信号实现原理图Fig.2 The principle of sin wave based on FPGA

通过已知的DAC转换精度，来确定等分数N，从而给出地址计数器的位数。将N等分点对应的时间值存入ROM表中，将时间值取出后经过数据处理，将其转换成对应于系统时钟f0的数据，如设T0=1/f0，为系统时钟周期，则tk时间点包含了M个系统时钟周期T0，这里，

并在此基础上根据 式（5）计算出所期望正弦信号对应的等分时间值tk′从而计算出其对应的系统时钟的个数M′=tk′/T0。然后通过定时器进行定时，定时到后进行累加当量“1”，并且给地址计数器输入信号使其地址加“1”。累加器输出的结果为标幺化的正弦信号，最后按照所需的正弦信号的幅值进行对应的处理，得到最终期望的正弦信号。

由于正弦信号具有对称性，很显然我们只需要做出Ts/4内的波形，利用它的对称性在程序内使之进行循环即可出现整个波形。

2 误差分析

下面对用本文方法生成的高精度数字化正弦调制信号进行误差分析。

根据以上所述原理，我们可以看出这种方法主要有两个误差来源源，下面我们对这两个误差来源进行分析。

第1种情况。假设q足够小，即：正弦调制信号数字化处理后二进制位数足够大，也就是说我们对幅值等分无穷多份，这正如我们所学过用多边形的方法来求圆的面积和周长的方法是类似的，那么我们得到的阶梯状的数字化正弦信号是和实际模拟正弦信号波形是趋近一致的。这个时候误差便产生在了FPGA系统时钟频率f0上。因为q量足够小意味着时间间隔△t=tk+1-tk也是无穷小，但系统时钟频率不是无限大。则这就造成下一个时间点已经到了，可系统时钟还没过一个周期，从而在本该在幅值加数字量“1”的时候却没加上，产生了误差。

那么这种情况就限制了生成数字化正弦信号的精度。因此，对于本文所提出的方法就要求正弦信号的频率fS与时钟频率f0之间要满足一定的关系如式（7）所示

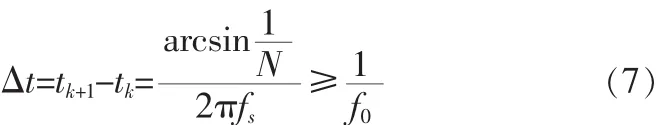
即在要获得的正弦信号最小的时间点不应该小于一个系统的时钟周期。

第2种情况。以上分析是假设数字化正弦波的位数足够大，事实上正弦波数字化处理之后，二进制的位数决定了量化误差的大小。我们不可能把位数定的太高，否则数据存储和处理都是不符合实际应用的。那么我们设定FPGA的系统时钟频率很小，进而分析由幅值等分有限造成的误差。

如图3所示，这时产生的误差的跳变沿如果发生在tk时刻时产生最大的误差为q；最小误差就是0。在一个阶梯波内，数字化正弦信号的误差范围为：

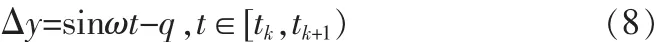
因此，可以比较直观地看出这种做法的数字化正弦波的误差的取值范围，在不计FPGA本身系统频率产生的误差下，则相邻两个时间点间产生误差在0～q之间。

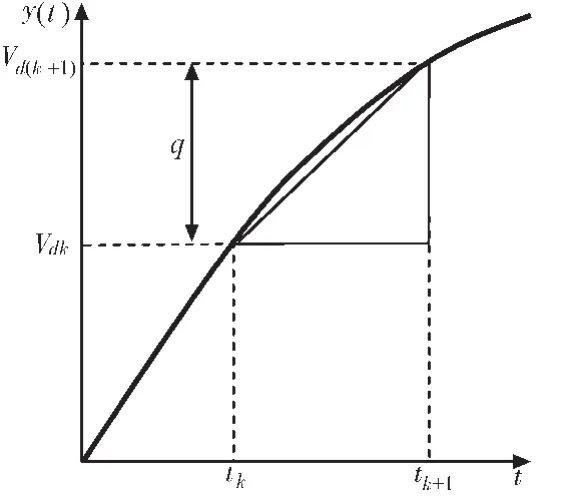
图3 幅值等分时误差分析原理图Fig.3 The analysis on error in amplitude equipartition

3 实验结果

本文采用Altera公司的开发软件QuartusⅡ，选用Cyclone II系列的EP2C8Q208C8 FPGA器件，根据本方法的原理，设计出了数字化正弦调制信号。系统时钟f0为48 MHz，设定的DAC转换精度为12位，则N取 2 047份，有2 048个等分时间点。设定正弦信号的频率fS为工频50 Hz。生成的数字化正弦调制信号经过DAC转化成模拟数字化正弦调制信号如图4所示。

图4 数字化正弦信号生成实验结果Fig.4 Experiment result of the digital sine wave

图中包括两组波形，上面为总体图，下面为上面的局部放大。图中，横坐标为时间，其中上图每格200 ms，下图每格5 ms，纵坐标为幅值，每格5 V。由下图可知，正弦调制信号的周期为20 ms。从图中可知道本文所提出的数字化正弦调制信号生成的新方法正确性。

4 结 论

本文根据正弦信号的幅值等分，提出了一种实时生成数字化正弦信号方法，并给出了其FPGA模块设计。对该方法的误差进行了分析，给出了这种方法的最大误差，证明这种方法的误差非常小。实验结果证明了该方法是实用可行的。

[1]Mwinyiwiwa B，Wolanski Z，Member，et al.Microproeessor implemented SPW M for multic0nverters with phase-shifted triangle carriers [J].IEEE Transactions on Indus-try A ppilcations，1998，34 （3）：487－494.

[2]彭力，林新春，康勇.数字控制高频变换器的新颖PWM方法[J].中国电机工程学报 ，2001，21（10）：47－51.

PENG Li，LIN Xin-chun，KANG Yong.New PWM methord of controling high-frequency converter[J].Proceedings of the CSEE， 2001， 21（10）：47－51.

[3]陈增禄 ，温宗周，钱慧芳，等.基于 MSPWM 的大功率宽频带低失真逆变器 [J].电力电子技术，2002，36（5）：22－24.

CHEN Zeng-lu，WEN Zong-zhou，QIAN Hui-fang，et al.A single-phase power inverterwith wide-band and lowdistortion based on MSPWM[J].Power Electronics，2002，36（5）：22－24.

[4]陈增禄，钱慧芳，温宗周，等.高精度宽频带逆变器直流漂移的多重采样频率控制方法研究 [J].电工技术杂志，2004，22 （10）： 72－75.

CHEN Zeng-lu， Qian Hui-fang，WEN Zong-zhou，et al.A novelmultiple sample frequencies controlscheme for compensating the output DC drift of a wide-band highprecision inverter[J].Electrotechnical Application，2004， 22（10）:72－75.

[5]毛惠丰，陈增禄，施杰.基于数字自然采样法的 SPWM波形生成研究[J].电力电子技术，2003，37（6）：76－78.

MAO Hui-feng，CHEN Zeng-lu，SHI Jie.Research on SPWM waveform formation based on digital nature sampling[J].Power Electronics，2003，37（6）：76－78.

[6]侯小华，施杰，毛惠丰，等.基于FPGA的高精度数字化正弦信号生成的新方法 [J].计算机测量与控制，2007，15（6）：824－840.

HOU Xiao-hua， SHI Jie， MAO Hui-feng，et al.Research of exact and digital sine wave generator based on FPGA[J].Computer Measurement&Control， 2007，15（6）：824－840.

[7]李建林，王立乔，李彩霞，等.基于现场可编程门阵列的多路 PWM波形发生器 [J].中国电机工程学报，2005，25（10）：55－58.

LI Jian-lin，WANG Li-qiao，LI Cai-xia.Multi-PWM pulse genrator based FPGA [J].Proceedings of the CSEE，2005，25（10）：55－58.

[8]周巧娣，黄继业.一种基于FPGA的正弦信号发生器的实验方法[J].实验室研究探索，2003，22（8）：82－84.

ZHOU Qiao-di，HUANG Ji-ye.An experimental method of sine-wave signal generator based on FPGA[J].Research and Exploration in Laboratory，2003，22（8）：82－84.

[9]李艳芳，陈增禄，詹佩，等.一种电压跌落补偿新拓扑及其跌落检测及补偿控制方法研究[C]//杭州：第十一届电力电子年会，2008.