多级穿廊结构坑道口部内爆炸冲击波传播规律的实验研究＊

王启睿，张晓忠，孔福利，张福明

（总参工程兵科研三所，河南 洛阳 471023）

近几场局部战争表明，在坑道口部内发生爆炸已成为可能。由于内爆炸产生的强冲击波具有峰值压力大、持续时间长、并将引起防护门后次生冲击波的特点，因此，它将对包括防护门在内的结构、设备和人员等均构成极大威胁。近年来，坑道口部内爆炸效应问题已引起高度关注。

穿廊结构是防护工程口部设置较典型的一种，该结构以其特有构型，通过穿廊与主坑道的T型转折能显著降低冲击波峰值压力。多次T型转折构成的多级穿廊结构，目前已被应用在坑道工程建设中，是网络式复杂坑道系统的基本构成部分［1－6］。随着武器性能和坑道工程建设的快速发展，现有成果已很难满足需求，而且，对整体功能更先进的网络化结构形式坑道及其基本结构单元——多级穿廊结构坑道的内爆炸冲击波效应的研究还不够，因此，积极开展对多级穿廊结构以及网络式复杂坑道系统机理研究，特别是实验研究十分必要。

本文中对多级穿廊结构中内爆炸效应进行系统的实验研究，给出多级穿廊结构中冲击波传播特性和峰值压力衰减规律，拟为地下工程建设部门提供一定的理论和实验依据。

1 实 验

典型的多级穿廊结构由多次T型转折的坑道构成，有几次T型转折称为几级穿廊，相应的坑道段依次为一级、二级、三级穿廊段和主坑道段，其中在主坑道段设置的防护门是坑道内最重要的防护设备之一。当发生口部内爆炸时，坑道内空气冲击波传播规律及门后坑道次生冲击波产生和发展规律是本项研究的重点。穆朝民等［7］就以上问题已经开展了大量的数值模拟工作并取得了一定成果，但还需通过开展系统的实验研究加以验证。

实验平台为链接式坑道模型系统，该系统由爆室和多个坑道单元按不同链接组合构成，连接部位密封并用高强螺栓加固，根据穿廊及其端部不同开闭情况分成多种工况。爆室与坑道材质相同，内截面尺寸为0.6m×0.6m，在爆室中心（坑道口部内）采用TNT集团装药，装药量为0.6～1.2kg，在沿坑道中轴线的侧壁面上布置测点，安装空压传感器进行测量。

整个研究过程中，根据不同工况和装药量共计进行60余炮次的实验，结构示意和及实际实验模型如图1所示。

2 结果分析

2.1 多级穿廊结构坑道冲击波传播规律

图1 实验模型示意图和现场布置Fig.1 Sketch drawings of test models and photos on the site

测得的典型波形如图2所示。对于一级穿廊结构，穿廊端部与爆室端部均封闭条件下比开口条件下的峰值压力明显升高，穿廊端部一端封闭时最大升高幅度接近10倍，两端都封闭时比一端封闭时高1.5倍。这说明，若穿廊结构的1个或2个出口遭到破坏倒塌封闭时，再发生内爆炸现象，则对主坑道的破坏效应将严重得多，故设计时一定要考虑穿廊端部破坏的极端情况。

对于二级穿廊结构，口部全开放情况下，内爆炸空气冲击波经过二级穿廊段的压力比经过一级穿廊段相应各点上的压力小得多，仅相当于30%左右；口部全封闭情况下类似，仅相当于28%左右。2种情况下，一级穿廊段的冲击波压力衰减都比二级穿廊段的快得多，如图3（a）所示。

对于三级穿廊结构发生口部内爆炸的情况也类似，口部全开放的情况下，空气冲击波经过二、三级穿廊段比一级穿廊段相应各点上的压力小得多，二级仅相当于一级穿廊段相应各点上压力的20%左右，三级仅相当于一级穿廊段相应各点上压力的5%左右；口部全封闭情况下，二级仅相当于一级穿廊段相应各点上压力的30%左右，三级仅相当于一级穿廊段相应各点上压力的7%左右。2种情况下，三、二、一级穿廊段的冲击波压力衰减速度依次减缓，如图3（b）所示。

图2 在等装药量、穿廊端部全开放的情况下，实验测得的部分波形Fig.2 Tested partial waveshapes in the cases of the same charge and all ends of gallery open

图3 多级穿廊冲击波衰减曲线Fig.3 Shock wave attenuation plots of multilevel gallery tunnels

根据以上分析，可将冲击波衰减状况按多级穿廊结构分叉的特点划分成多个作用区段：第Ⅰ区段为一级穿廊分叉前，属爆炸冲击波直接作用区域，为后续结构的入射冲击波，强度高、持续时间短；第Ⅱ区段为第Ⅰ区段后到二级穿廊分叉之间，由原入射冲击波分成2支，一支沿一级穿廊段传播，另一支形成二级穿廊段入射波，2段的冲击波强度较入射波都已明显降低；第Ⅲ区段为第Ⅱ区段后到三级穿廊分叉之间，类似第Ⅱ区段，由二级穿廊段入射波分成2支，一支沿二级穿廊段继续传播，另一支形成三级穿廊段入射波，冲击波的强度降低更明显，作用时间也相应延长；同理可推，如再有多次分级，则区段划分及其变化规律均与此类似。冲击波的分流过程如图4所示，因此口部内爆炸产生的强冲击波经过多级穿廊的分流消减，到达主坑道防护门时强度已经显著降低，消波效果显著。

图4 多级穿廊冲击波衰减区段的衰减曲线和对应的坑道示意图Fig.4 Attenuation stage of shock wave in the multi－level gallery tunnel

2.2 防护门上荷载规律

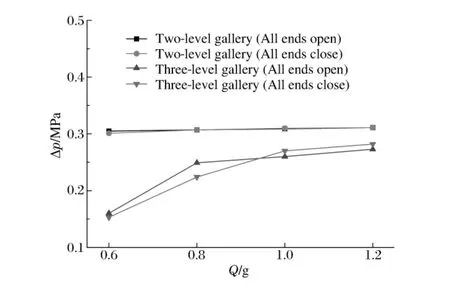
图5 不同药量防护门上荷载变化Fig.5 Load on the protective door under unequal charges

防护门设置于主坑道内，距离上一级穿廊结构很近，经过多级穿廊分流消减的强冲击波到达时强度已经显著降低，但仍有一定作用，特别是当穿廊设置较简单或者内爆炸强度较大时，对防护门上的冲击波荷载仍然较强。实验结果表明：相同药量、不同的穿廊结构之间，一级穿廊结构防护门上的压力明显大于二级穿廊结构，二级的明显大于三级的；相同药量、相同穿廊结构而不同的端口开闭情况下，整体上各端部全封闭时防护门上压力稍大，但不同工况之间相差不很明显。如图5所示，二级和三级在较小药量时压力差值为约0.15MPa，在较大药量时压力差值为约0.05MPa。防护门上荷载变化也说明多级穿廊结构的显著消波作用，如果再设置一定的防护门的防护措施，能将荷载降到更安全的范围。

2.3 防护门后主坑道次生冲击波的变化

坑道内强空气冲击波作用在防护门及门墙上时，通过高速强动力学作用引发门的振动与门后空气的压缩并推动压缩波传播，形成次生冲击波。当振动强烈或多次振动的频率叠加时，次生冲击波会明显增强，如图6所示，次生冲击波强度超过一定域值，亦可对人员或设备产生杀伤破坏作用。

图6 门后次生冲击波的形成Fig.6 Generation of secondary shock waves behind protective door

实验研究表明，相同装药量情况下，三级穿廊结构主坑道防护门后次生冲击波压力仅相当于二级穿廊结构的36%，次生冲击波强度较低，持续时间较长，趋于稳定。可见，三级穿廊结构与二级穿廊结构相比，对防护门后次生冲击波强度有更好的抑制效果，如图7所示。

2.4 与直坑道工程量比较

地下防护工程的早期设计与建筑中，主要通过长度延伸来降低冲击波强度，即便是使用一级长穿廊结构，同时仍依靠大量增加主坑道长度等来达到有效减波目的。随着武器的发展，单纯依靠长度延伸的方法已越来越不适应现实需求，长直坑道效率较低、防护性能弱、维护投入大、容易造成空间浪费，而且施工时工程量较大，不经济。

图7 次生冲击波变化规律Fig.7 Change of secondary shock waves

对于相同装药量的口部内爆炸，要达到同样的冲击波衰减量，则在多级穿廊结构的每一段坑道都比直坑道的长度缩短很多，如图8所示，依次通过三级穿廊段与直接通过直坑道达到相同压力值时，穿廊结构的比例距离仅相当于直坑道的50%左右。可见，三级穿廊结构的实际工程量相对于直坑道会大幅降低，因此，多级穿廊结构还具有显著的经济性。

3 结 论

图8 不同坑道工程量对比Fig.8 Comparison between engineers of different tunnels

（1）内爆炸情况下，穿廊结构坑道口部的开闭不同对坑道中冲击波峰值压力的影响很大，其中，全开放时相当于一端封闭时的60%，而一端封闭时最低仅相当于两端全封闭时的10%。

（2）多级穿廊结构对内爆炸情况下的坑道内冲击波峰值压力降低效果明显，穿廊段数越多，降低效果越显著。口部全开放情况下，二级穿廊段的压力仅相当于一级穿廊段相应各点的20%～30%，而三级穿廊段的压力仅相当于一级穿廊段相应各点的5%左右；口部全封闭情况下，二级穿廊段的压力仅相当于一级穿廊段的28%～30%，而三级穿廊段的压力仅相当于一级穿廊段相应各点的7%左右。

（3）多级穿廊结构对降低内爆炸情况下主坑道防护门上的荷载和门后次生冲击波强度很有利，能有效减弱对防护门及内部人员设备的毁伤效应，使结构在获得较好防护性能的同时还能大量减少实际工程施工量，三级穿廊结构相对于直坑道达到相同冲击波衰减幅值时，工程量减少约50%。

［1］United States Army.TM5－855－1：Fundamentals of protective design for conventional weapon［S］.1992.

［2］Atsushi A，Kazuyoshi T.Study of attenuation of shock waves propagating over arrayed spheres［C］∥Proceedings of the 24th International Congress on High－Speed Photography and Photonics.Sendai，Japan，2000：24－29.

［3］杨科之，杨秀敏.坑道内化爆冲击波的传播规律［J］.爆炸与冲击，2003，23（1）：37－40.YANG Ke－zhi，YANG Xiu－min.Shock waves propagation inside tunnels［J］.Explosion and Shock Waves，2003，23（1）：37－40.

［4］庞伟宾，何翔，李茂生，等.空气冲击波在坑道内走时规律的实验研究［J］.爆炸与冲击，2003，23（6）：573－576.PANG Wei－bin，HE Xiang，LI Mao－sheng，et al.The formula for airblast time of arrival in tunnel［J］.Explosion and Shock Waves，2003，23（6）：573－576.

［5］张德良.爆炸波在复杂结构抗道内传播的数值模拟［J］.计算力学学报，1997，14（增刊）：189－192.ZHANG De－liang.Numerical simulation on blast wave propagation in the complex tunnel［J］.Journal of Computational Mechanics，1997，14（Suppl）：189－192.

［6］李秀地，郑颖人，李列胜.坑道中化爆冲击波入射压力传播规律的研究［J］.防护工程，2005，27（3）：6－10.LI Xiu－di，ZHENG Ying－ren，LI Lie－sheng.Study on propagation law of incident shock wave pressure produced by chemical explosives in tunnel［J］.Protective Engineering，2005，27（3）：6－10.

［7］穆朝民，辛凯，任辉启，等.爆炸冲击波在 T形坑道内传播规律的数值研究［J］.防护工程，2008，30（3）：32－35.MU Chao－min，XIN Kai，REN Hui－qi，et al.Numerical investigation on blast wave propagation in the T－tunnel［J］.Protective Engineering，2008，30（3）：32－35.