基于RJMCMC方法的水下被动目标声源数和方位联合估计
2011-09-19钊1刘郑国2王海燕1申晓红1斌1
陈 钊1, 刘郑国2, 王海燕1, 申晓红1, 和 斌1
基于RJMCMC方法的水下被动目标声源数和方位联合估计
陈 钊, 刘郑国, 王海燕, 申晓红, 和 斌
(1. 西北工业大学航海学院, 陕西西安, 710072; 2. 中国船舶重工集团公司, 北京, 100097)
针对传统的子空间类宽带信号处理方法需要较多的信号快拍数才能取得较好的估计效果这一问题, 本文将一种基于时域宽带信号模型的贝叶斯高分辨估计方法用于水下被动目标的方位估计(DOA)。该方法使用宽带信号的时域模型, 依据贝叶斯准则构建所需参数的后验概率密度函数, 并采用可逆跳变马尔科夫链蒙特卡罗(RJMCMC)方法执行贝叶斯计算, 对后验概率密度函数进行峰值搜索。由于其能够在不同维的参数空间中跳转, 因此可以进行模型阶数(声源数)和目标方位的联合估计。与传统的子空间类方法相比, 这一方法能直接在时域进行信号处理且仅需显著较少的信号快拍数。仿真结果表明, RJMCMC算法能较好地估计出声源数和目标方位。
被动目标方位估计; 时域宽带模型; 贝叶斯高分辨; 模型阶数检测; 可逆跳变马尔可夫链蒙特卡罗(RJMCMC)
0 引言
精确定位远场中相距很近的多个声源是水声信号处理中的关键问题之一。传统的波束形成法受到瑞利限的制约, 分辨率很低。最大熵谱法和最小方差法是对常规波束形成法的简单修正, 但两者在估计性能上没有大的突破。子空间类方法极大地突破了瑞利限的制约, 使高分辨目标方位估计方法向前迈进了一大步, 但是在低信噪比, 少快拍, 信号源相关以及存在系统误差时, 此类方法的性能会受到很大的影响。最近十几年, 贝叶斯高分辨方位估计方法受到普遍关注并被广泛地研究。贝叶斯高分辨方位估计技术是利用信号和噪声的联合后验概率密度函数对信号进行谱估计的一种方法。Lasenby和Fitzgerald最早在文献[1]中提出了这种方法。它利用贝叶斯定理把待估计量看作是随机变量, 引入被估计量的先验概率, 因而改善了估计的性能。之后不同学者对贝叶斯高分辨方位估计方法进行了探索和改进, 提出了许多新的改进。
对于水下目标的检测、方位估计和跟踪问题, 与主动探测方式相比, 被动方式具有更好的隐蔽性。被动探测方式利用水下目标的辐射噪声进行处理, 通常涉及宽带信号处理问题。传统的基于子空间类的高分辨方位估计方法常需要较多的快拍数且在频域内进行处理。被广泛使用的相干信号子空间方法(coherent signal subspace method, CSSM)需要方位预估, 其准确性严重影响到了目标方位估计的精度。
本文引入文献[4]中提出的一种时域宽带信号模型, 利用水下被动目标的辐射噪声进行目标方位估计。首先得到基于贝叶斯模型的声源数和目标参数的联合后验概率密度函数。贝叶斯高分辨方位估计方法需要对此概率密度函数进行多维搜索, 随着待估计参数维数的增加, 计算量呈指数增长, 为此许多文献提出使用可逆跳变马尔可夫链蒙特卡罗(reversible jump Markov chain Monte Carlo, RJMCMC)方法进行后验概率密度函数的峰值搜索。同时采用文献[4]中的最大后验(maximum aposterior, MAP)声源恢复方法可以求得各个声源的幅度。
本文将文献[4]的时域宽带信号模型和RJMCMC的方法结合起来用于水下被动目标的声源数和方位的联合估计。在较少的快拍情况下可以取得较好的估计精度, 且在估计出目标方位(direction of arrival, DOA)的同时可以进行声源数检测和声源幅度恢复。仿真结果表明了此方法的有效性。
1 基于时域宽带信号模型的贝叶斯高分辨DOA估计方法
本节简述文献[4]提出的时域宽带信号模型。这一模型采用插值函数表示阵列接收的宽带信号, 使得算法只需在时域内进行处理, 避免了传统的聚焦类方法在频域内处理的缺点, 从而无需对阵列信号进行傅里叶变换。
1.1 时域宽带信号模型
假定有元均匀线列阵(uniform linear array, ULA),个远场声源s(t)分别从θ,=0,…,-1 入射, 声源s(t)为有限带宽的宽带或窄带信号, 其频率响应和带宽分别为
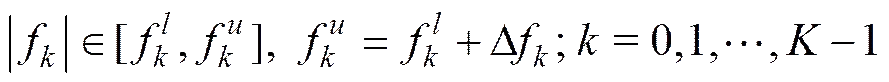
当声源入射方位角≤π/2时, 阵元1首先接收到信号, (-1)τ时延之后阵元才接收到信号, 如图1所示。声源s()在第个阵元上产生的信号可以表示为
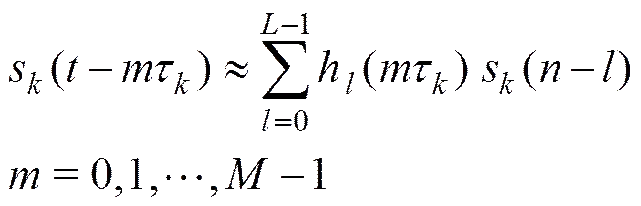
其中:τ为第个声源信号的阵元间延迟(inter sensor delay, ISD), 定义如下
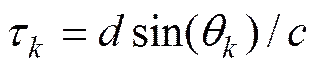
式中:为水中声速;为均匀线列阵的阵元间距;(mτ)是对应于时延mτ的插值序列的第l个元素, 采用加权sinc函数作为插值序列, 其中(l-)为汉明窗,为归一化时延值
(4)
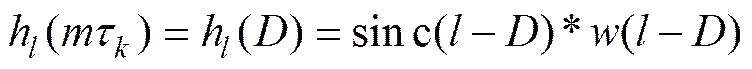
(6)
式中,f是系统的采样频率, 满足
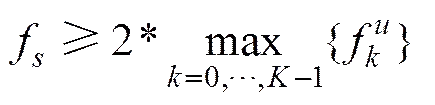
阵元间距满足式(8) (其中为可能的最大目标声源频率成分), 本文取=c/f
(8)
由式(3)和式(8)可知
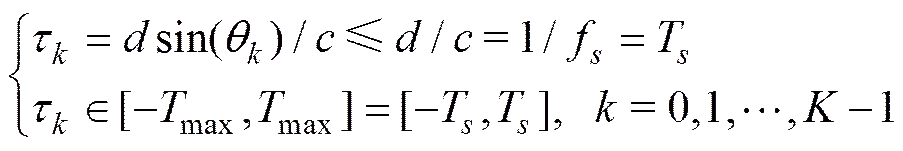
(10)
写成矩阵-向量形式为
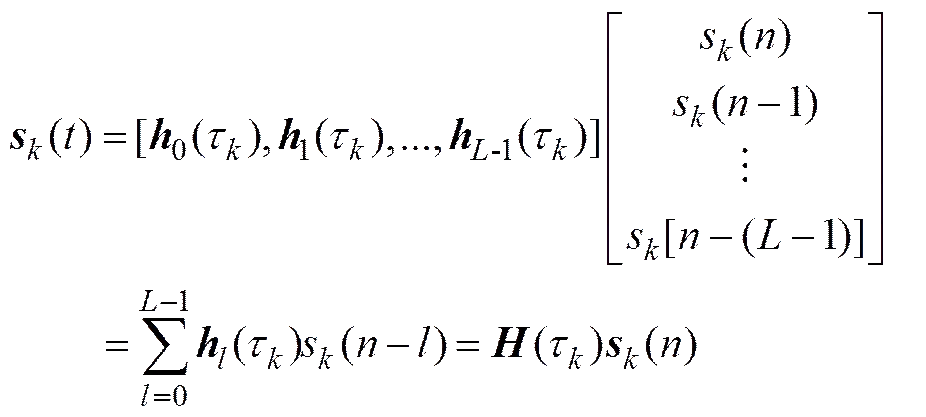
因此
(12)
式中:()∈R×是第l个插值矩阵;[,,…,τ]∈R为与声源入射方位相对应的时延向量;∈R是次快拍时刻的声源幅度向量;∈R是次快拍时刻服从(0,I)分布的高斯白噪声。最终定义一个向量∈R
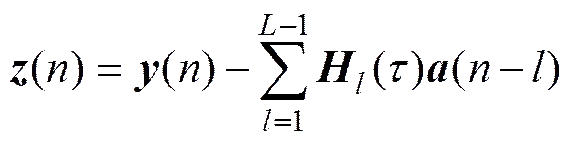
它可以看作是快拍与其基于插值逼近之间的误差, 可写作
(14)
对于入射方位角>π/2的情况, 阵元首先接收到入射信号, (-1)τ时延之后阵元1才接收到信号, 如图2所示。
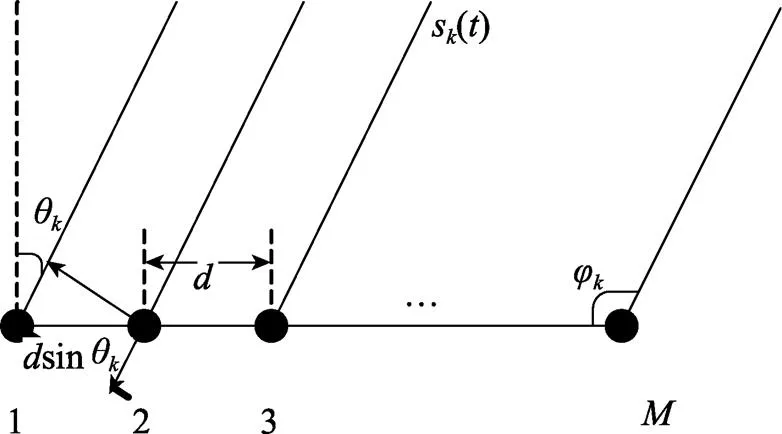
图2 入射角φk>π/2时的阵列信号接收模型
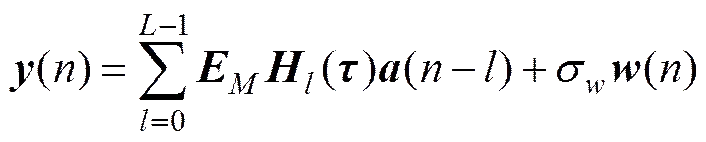
式中:为一个交换矩阵, 它交换矩阵()的每一行
(16)
重新定义插值矩阵为

重写时域宽带信号模型
(18)
1.2 贝叶斯后验概率密度函数
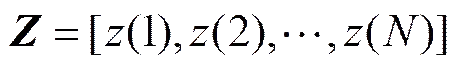
对于所有的快拍, 全似然函数为
(20)
式中,为真实声源数的一个估计。由此通过贝叶斯理论, 声源参数的后验概率密度函数可以表示为全似然函数和声源参数先验函数的乘积
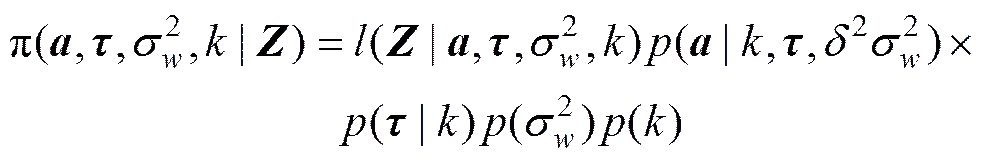
式中,是一个超参数, 它与信噪比有密切关系。声源幅度先验的选取同文献[4],选为均匀先验
(22)
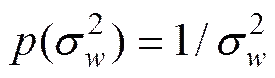
的先验选择为期望值Λ为的泊松分布, 其中Λ是期望的声源数
(24)
对于上述各参数, 人们感兴趣的是声源数和声源时延。将式(22)~式(24)代入式(21), 并把“多余”参数和积分掉,可以得到
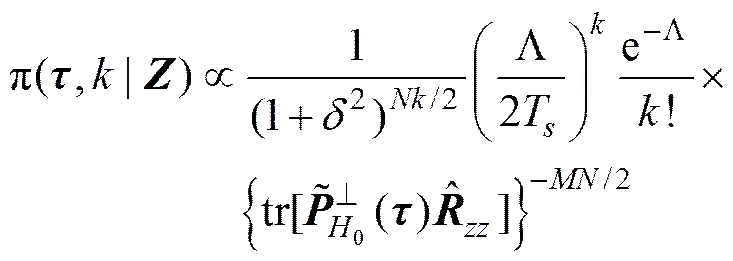
其中
(26)
式(25)即所需参数和的联合后验概率密度函数, 通常需要对后验概率密度函数进行多维峰值搜索, 最大峰值所对应的时延和模型阶数值便是入射声源的DOA和数目。传统峰值搜索方法计算量很大, 基于马尔可夫链蒙特卡罗(MCMC)的方法可以大大地减少运算量。
2 基于RJMCMC算法的贝叶斯高分辨方位估计
研究的目标是在贝叶斯框架下进行联合模型选择(声源数估计)和参数估计, 即通过最大化式(25)来求得声源数和时延。通常采用的方法是RJMCMC算法。
传统的RJMCMC方法由3种不同的运动组成: 更新运动(update move)、消失运动(death move)和产生运动(birth move)。
每次迭代执行上述3种运动的概率分别为u,d和b, 它们由式(27)确定, 其中为每次迭代模型阶数变化的概率, 通常选取为=0.5,()为式(24)中服从期望为Λ的泊松分布
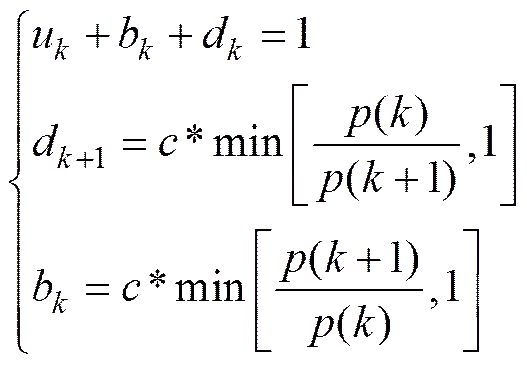
在RJMCMC算法的每次迭代中, 从与上述运动对应的3种不同的建议分布中抽取候选样本。假定第次迭代的样本为(,)
(28)
1) 更新运动: 此时声源数固定不变, 仅更新时延向量值。本文选取以为均值, 以为方差的高斯分布作为建议分布, 从中抽取候选样本~(,)。
2) 产生运动: 当<时有效。其中,为最大允许的声源数(本文选取为6)。此时从分布[T,T]中随机抽取一个样本´, 并且加入上次迭代的样本中成为候选样本。
3) 消失运动: 当>1时有效。此时从上次迭代的样本中随机地去除一个时延值, 然后将新的时延组合作为候选样本, 假设第个时延值被随机地去除。
(30)
于是候选样本以如下概率被接受
其中:和分别表示上次迭代值和本次候选值,(|)为建议函数。在本文的仿真中, 为了简化, 候选样本以下列概率被接受
(32)
这样不仅简化了运算, 并且在RJMCMC算法的迭代过程中样本总是尽量向着更高的概率区域跳转。迭代结束之后以最后一个样本值作为最终的声源数和方位估计的结果。于是一个简化的RJMCMC算法的可概括为以下步骤。
1) 初始化, 从均匀分布[1,]中随机第选取初始模型阶数; 从与对应的均匀分布[T,T]中抽取初始时延值。
2) 第次迭代, 从均匀分布[0,1]中抽取随机数, 并且利用式(27)计算各个运动被执行的概率u, d和b。若u<u则执行更新运动, 若≤≤d+u则执行消失运动, 否则执行产生运动。
3) 使用产生的候选样本和上次迭代样本值, 依据式(29)计算样本的接受概率。若样本被接受, 则; 否则。
4) 如此迭代下去直到迭代终止。
5) 将最后一次迭代值作为声源数和方位估计的结果。
3 水下目标辐射噪声模型
对于诸如舰船, 潜艇和鱼雷等主要的水下水面目标, 它们都具有许多往复运动的机械部件, 这些部件所产生的振动辐射声波到海水中便形成目标的辐射噪声。目标辐射噪声具有特殊重要性, 被动声纳就是利用其特性从自噪声或环境噪声背景上把它区分出来。按照噪声源的不同它可以分为3类: 机械噪声, 螺旋桨噪声和水动力噪声。其中前2类在多数情况下是主要的噪声源, 舰船噪声就是这3类噪声中连续谱成分和线谱成分的迭加。本文采用文献[9]的方法产生阵列接收宽带信号来仿真水下被动目标的辐射噪声。如图3给出了简化的3个水下目标辐射噪声的功率谱模型。
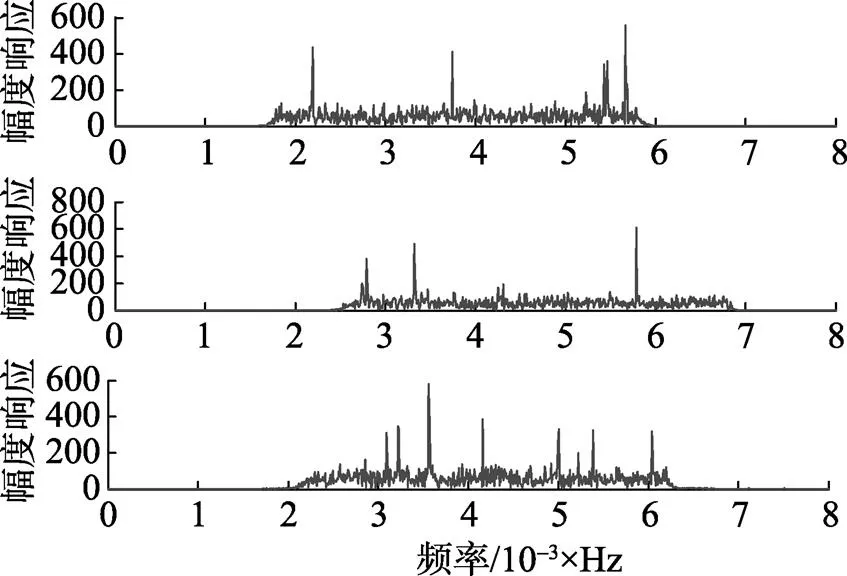
图3 水下目标辐射噪声功率谱模型
4 计算机仿真
采用如下仿真条件。使用=10元ULA, 相应波束宽度为=10.09°。信号快拍数为=64。考虑稍复杂的3个声源的情况, 都具有相等的信噪比(signal-to-noise ratio, SNR)。声源信号的入射角分别为=6.00°,=12.00°和=18.00°, 两两间的间距接近半个波束宽度。宽带声源的频谱范围为∈[900, 2 900] Hz,∈[1 300, 3 400] Hz和∈[1 100, 3 100]Hz。系统采样频率f=8 000 Hz。水下声速为=1 500 m/s, 阵元间距为f= 0.187 5 m。仿真参数详见表1。
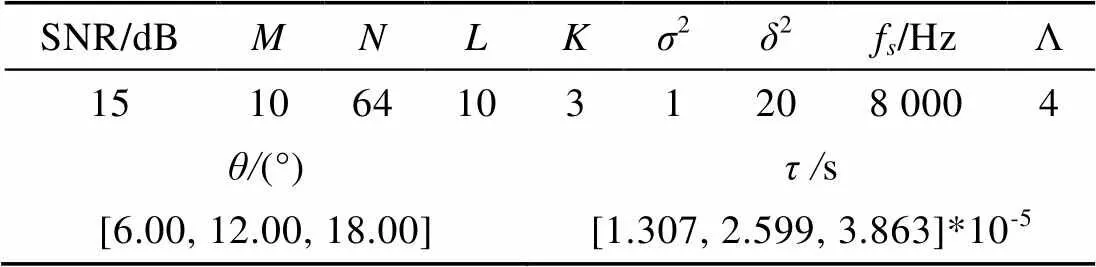
表1 仿真采用的参数值
采用表1的参数进行仿真, 图4、图5和图6给出了单次运行使用RJMCMC算法时贝叶斯高分辨水下被动目标方位估计方法(wide band Bayesian estimation method,WBBEM)的性能。为了程序运行效率, 本文中RJMCMC算法仅采用200次迭代。
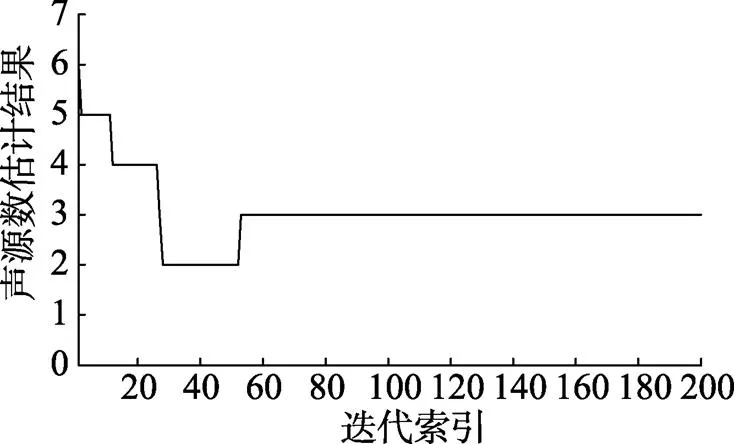
图4 单次运行时算法的声源数估计结果
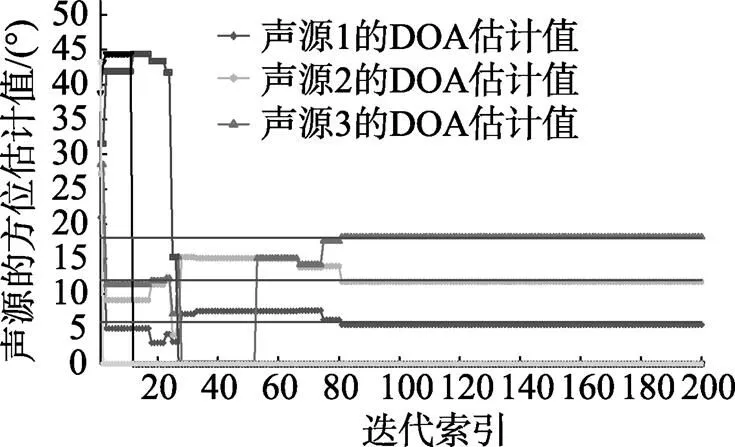
图5 单次运行时算法的方位估计结果
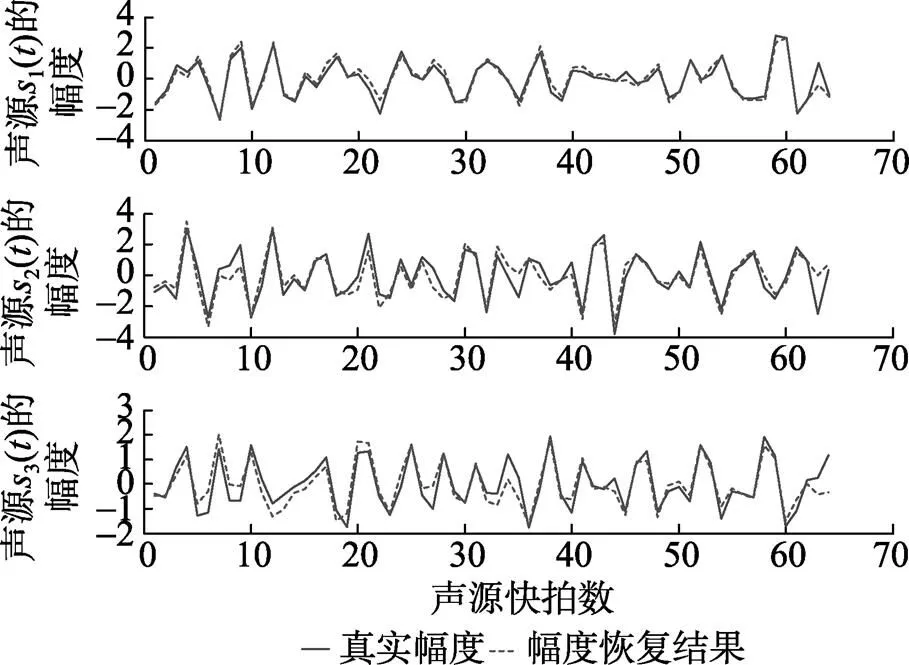
图6 单次运行时算法的声源幅度恢复结果
图4给出了算法声源数估计的收敛结果。由图可知, 算法收敛相当迅速, 从第55次迭代算法便正确地估计出了入射声源数。并且由多次独立仿真可以看出, 大多数时, 算法在30次迭代之内便能正确地估计出声源数为3。
图5给出了单次运行时算法的方位估计结果。由图可以看出, 在迭代算法结束时, 3个入射声源方位都能被较为精确地估计出来。
图6给出了采用MAP算法的声源幅度恢复结果, 由图可知, 3个声源的幅度都被较好地恢复出来, 这能为后续的基于频谱估计的目标识别打下基础。
图7~图9给出了采用表1中的参数进行100次独立蒙特卡罗(MC)仿真时RJMCMC算法的性能。图7给出了进行100次独立MC仿真时声源数估计值的分布。由图可以看出, 在100次独立仿真中, 有83次算法正确地估计出入射声源数为3阶, 其余17次倾向于低估声源数, 且估计结果均为2。
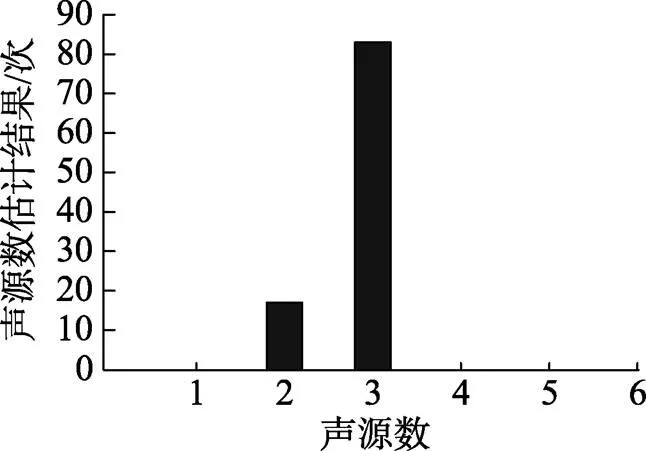
图7 进行100次独立蒙特卡洛仿真的声源数估计结果
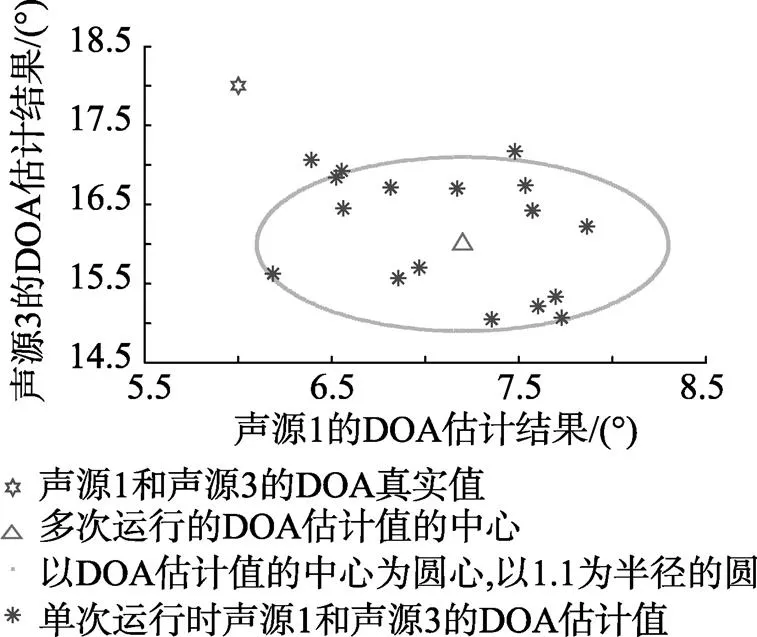
图8 声源数估计值为2时的方位估计结果
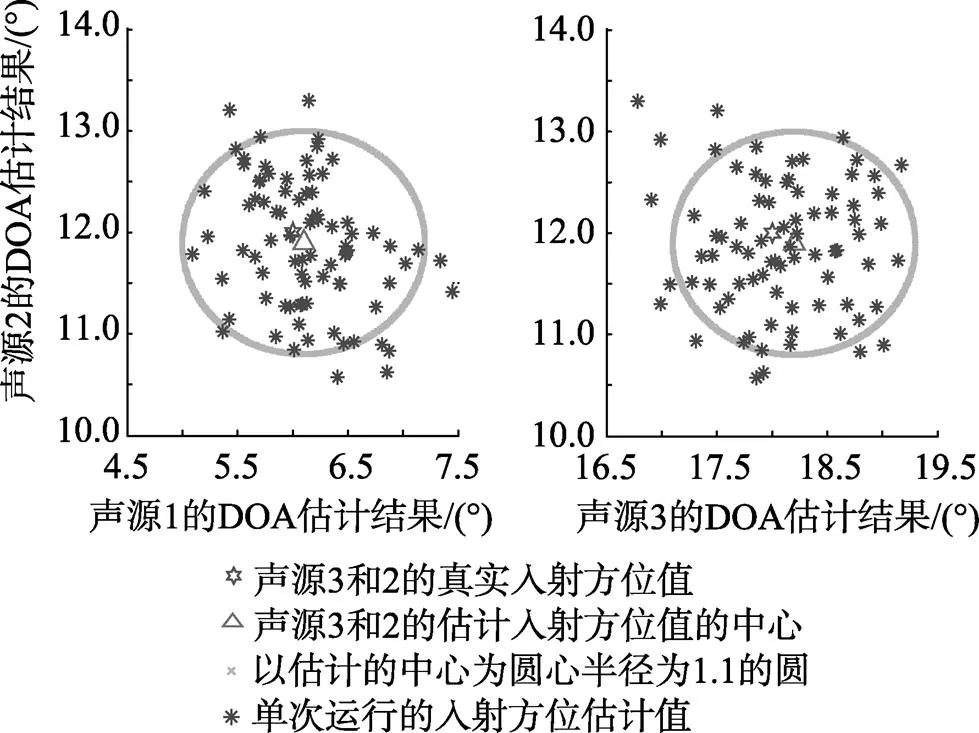
图9 声源数估计值为3时的方位估计结果
图8给出了声源数估计值为2时的DOA估计结果。由图可以看出, 在这17次独立蒙特卡罗仿真中, 算法总是大致地估计出了声源1和3而遗漏了声源2, 且声源1的角度估计值倾向于偏大而声源3的角度估计值倾向于偏小。由此可以看出具有相同信噪比的3个声源中处于中间位置的声源的估计受到了其两侧声源的干扰, 同时两侧声源的DOA估计结果同样受到了中间声源的影响而趋于向其靠近。图中三角形的方位估计值中心相对于六角星的真实方位值明显地向右下侧偏移清晰地表现了这一趋势。
图9给出了正确地估计出声源数3时的DOA估计结果。为了表述方便, 分别绘出声源1和2, 声源2和3的DOA估计结果。由图可以看出单次运行的DOA估计值(星形)绝大多数都集中地分布在真实的DOA值(图中用六角星表示)附近, 其中心位置(图中用三角形表示)稍有偏离。声源1和2的估计值中心约为[6.1°,11.9°]; 而声源2和3的估计值中心约为[11.9°,18.2°]。由此可见算法很好地估计出了3个声源的方位, 具有较好的性能。
表2给出了不同信噪比下, 采用RJMCMC算法的声源数估计结果和方位估计的均方根误差。本文出于程序运行的简便采用的迭代次数偏少(仅200次), 因此对于声源数的估计无法达到很理想的效果; 但是一旦算法采用了较多的迭代次数(例如1 000次以上), 则声源数的估计性能将会得到改善。
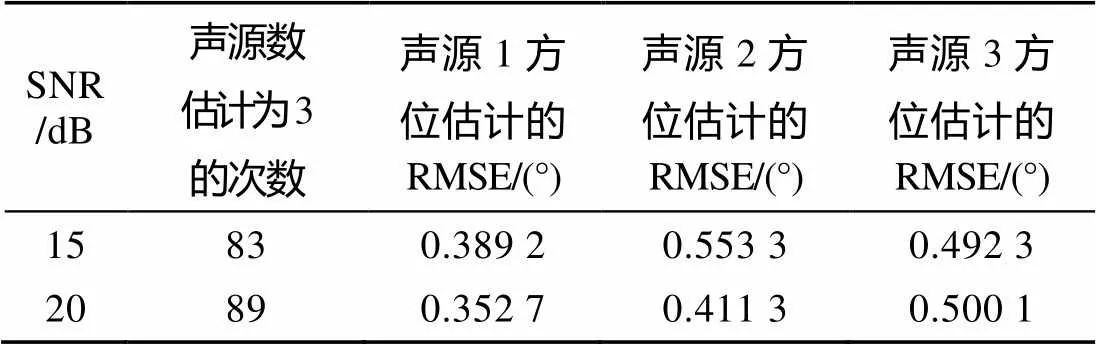
表2 不同信噪比下声源数估计结果及方位估计均方根误差
5 结束语
最近10年贝叶斯高分辨技术越来越广泛地应用到目标方位估计中, 在低信噪比, 少快拍和信源间隔很近的情况下取得了比子空间类方法高得多的方位估计精度。
本文将文献[4]中提出的基于时域宽带模型的贝叶斯高分辨方位估计方法引入水下被动目标方位估计当中, 在水下目标辐射噪声的宽带表征中采用了插值矩阵表示方法。与传统的处理宽带信号的聚焦类子空间方法相比, 本文方法具有显著的优势。首先, 它可以直接在时域内进行信号处理; 其次, 它在信号快拍数较少的情况下也能取得较好的估计结果, 而相比之下聚焦类宽带方法在少快拍情况下性能会急剧恶化; 最后, 它可以在进行方位估计的同时进行模型阶数(声源数)的检测和声源幅度的恢复, 而没有显著地增加计算量, 其中信号幅度的恢复有助于基于谱估计的目标识别。
本文采用RJMCMC算法对求得的目标声源数与目标参数的联合后验概率密度函数进行峰值搜索。并且选取了较复杂的3个目标辐射声源的情况进行计算机仿真。仿真结果显示WBBEM算法不仅能够较准确地估计出目标辐射声源数, 同时可以较为精确地估计出目标方位, 并且声源幅度也能被很好地恢复出来, 取得了较好的估计效果。
[1] Lasenby J, Fitzgerald W J. A Bayesian Approach to High Resolution Beamforming[J]. Radar and Signal Processing, IEEE Proceedings F, 1991, 138(6): 539- 544.
[2] Huang J G, Sun Y. A New Gibbs Sampling DOA Estimator Based on Bayesian Method[J]. Acoustic, Speech and Processing, 2003(5): 229-232.
[3] Sun Y, Liu K W, Huang J G, et al. Bayesian DOA Estimator by Gibbs Sampling[J]. Computer Engineer- ing and Applications, 2002, 38(12): 36-38.
[4] William N, Reilly J P, Kirubarajan T, et al. Wideband Array Signal Processing Using MCMC Methods[J]. IEEE Transactions on Signal Processing, 2005, 53(2): 411-426.
[5] Andrieu C, Doucet A. Joint Bayesian Model Sele- ction and Estimation of Noisy Sinusoids Via Rever- sible Jump MCMC[J]. IEEE Transactions on Signal Processing, 1999, 47(10): 2667-2676.
[6] Green P J. Reversible Jump Markov Chain Monte Carlo Computation and Bayesian Model Determina- tion[J]. Biometrika, 1995, 82(4): 711-732.
[7] Larocque J R, Reilly J P. Reversible Jump MCMC for Joint Detection and Estimation of Sources in Colored Noise[J]. IEEE Transactions on Signal Proce- ssing, 2002, 50(2): 231-240.
[8] 于红旗, 刘剑, 黄知涛, 等. 阵列接收宽带信号的建模方法及仿真[J] . 电子对抗, 2006(4): 7-12.
[9] William N, Reilly J P, Kirubarajan T. Wideband Array Signal Processing Using Sequential Monte Carlo Methods[R]. Department of Electrical and Co- mputer Engineering, McMaster University, 2003: 1-28.
(责任编辑: 杨力军)
Joint Estimation of Source Number and DOA for Underwater Passive Target Based on RJMCMC Method
CHEN Zhao, LIU Zheng-guo, WANG Hai-yan, SHEN Xiao-hong, HE Bin
(1.College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China; 2.China Shipbuilding Industry Corporation, Beijing 100097, China)
Conventional wideband signal processing method of subspace class wideband requires more snapshots to get a better estimation result. We apply a Bayesian high resolution direction of arrival(DOA) estimation method based on the time-domain wideband signal model to underwater passive target DOA estimation. Compared with conventional subspace class methods, the proposed method can process signal directly in time-domain and needs remarkably less snapshots. We use a time-domain wideband signal model to construct a posterior probability density function(PDF) of the parameters according to Bayes law, and then use the reversible jump Markov chain Monte Carlo(RJMCMC) method for Bayesian estimation to search peaks of the posterior PDF. This method can jump among parameter spaces with different orders, thus can implement joint model order (i.e. source number) and DOA estimation. Simulation results show that the RJMCMC method exhibits good performance in joint estimation of model order and DOA.
passive target direction of arrival (DOA) estimation; time-domain wideband model; Bayesian high resolution; model order detection; reversible jump Markov chain Monte Carlo (RJMCMC)
TJ630.34; TN911.7
A
1673-1948(2011)06-0415-08
2011-03-17;
2011-05-19.
国家自然科学基金(60972153), 博士点基金(20096102110038), 西北工业大学基础研究基金(NPU-FFR-JC201004).
陈 钊(1983-), 男, 在读博士, 研究方向为水下目标的识别、方位估计与跟踪.
