基于线性最小二乘估计的双基地声纳定位优化算法
2011-09-19刘若辰王英民
刘若辰, 王英民, 张 群
基于线性最小二乘估计的双基地声纳定位优化算法
刘若辰, 王英民, 张 群
(西北工业大学航海学院, 陕西西安, 710072)
针对双基地声纳系统存在冗余信息的问题, 基于线性最小二乘估计理论提出了一种定位优化算法, 建立了型声纳系统水下定位的数学模型。通过MATLAB软件的仿真分析, 给出了影响该算法性能的各个因素, 并与传统TOL算法进行了对比。仿真结果表明, 采用线性最小二乘估计算法能更好地利用系统测量的冗余信息, 显著提高双基地声纳基线区和侧边区的定位精度。该算法具有受基线长度和站址误差影响小等优点, 是一种具有工程应用价值的双基地声纳定位算法。本文的研究可为多基地声纳定位优化问题的研究提供理论基础。
双基地声纳; 线性最小二乘估计; 定位精度; 信息冗余
0 引言
双基地声纳, 由于收发设备分置, 系统具有主动和被动声纳工作的特点, 能有效利用现有的技术和设备, 在反潜作战和水声对抗方面具有很大的优势, 因而受到世界主要军事强国的极大关注, 并成为新一代声纳技术研究的重要课题。
为了解决双基地声纳系统的定位性能优化问题, 需要把冗余的观测信息充分利用, 并扩大双基地声纳系统的使用域, 以充分发挥该系统高精度定位的优势。为此, 根据双基地声纳的工作特点, 提出一种基于线性最小二乘估计的优化算法, 通过与传统定位算法的对比, 证明了该算法在基线区和侧边区的优越性。
1 线性最小二乘定位算法数学模型
1.1 定位原理
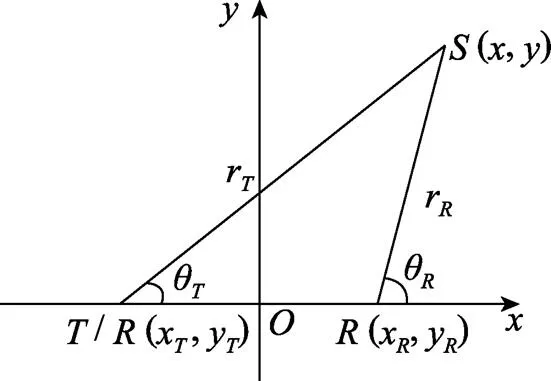
图1 双基地声纳系统配置几何关系
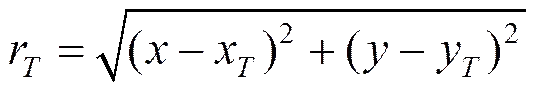
(2)
(3)

(5)
下面利用LLS算法, 将测量信息经过简单的数学变换, 构成线性方程组的形式对目标位置进行估计。将式(1)~式(4)去掉关于目标位置的2阶项, 得

,(7)
将方位角的数学表达式展开得
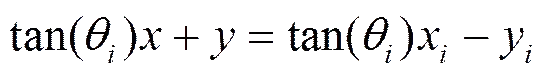
再将式(6)、式(8)写成线性方程组的形式
(9)
将上式写成如下形式

用伪逆法可求得目标的估计值为
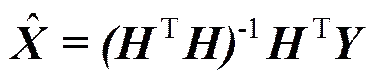
1.2 定位误差分析
对式(1)~式(4)求全微分可得
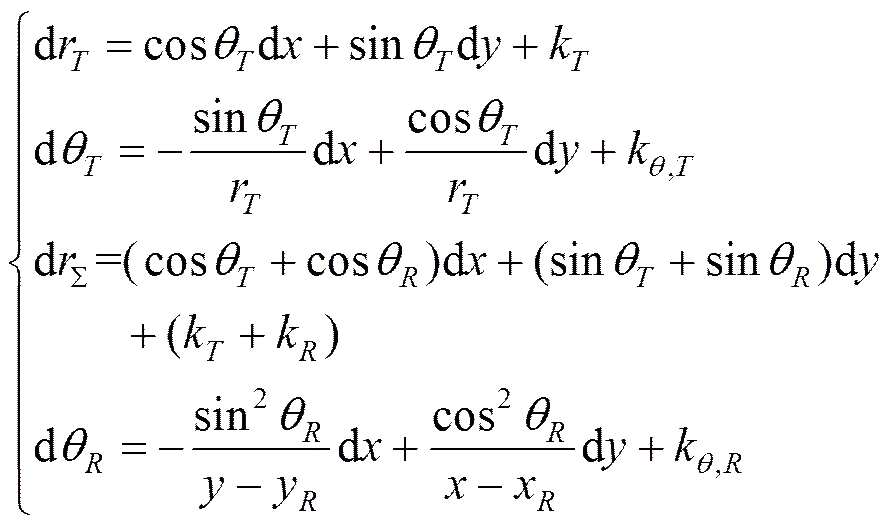
(13)
将式(12)写成矩阵形式
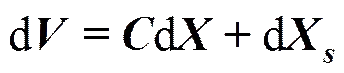
式中
用伪逆法可计算LLS方法估计误差矩阵

定位误差的协方差矩阵
(16)
在2D情况下, 双基地声纳系统对目标的定位精度可以用水平方向上定位误差方差和的平方根表示, 由于这个参数与目标及发射站和接收站的相对几何位置有关, 因此称为定位误差几何分布(geometrical dilution of precision, GDOP), 对于LLS算法,的表达式为
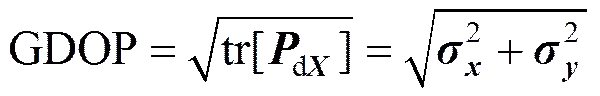
2 数值仿真
2.1 仿真条件
根据上述算法, 对双基地声纳系统的定位性能进行仿真。仿真参数设置为:站坐标为,,站坐标,, 水中声速为v=1.5 km/s,测量误差为,,,。目标探测范围:方向,方向。
2.2 仿真结果及分析
图2~图5所示分别为改变基线长度, 时间测量误差, 角度测量误差和站址测量误差时系统的定位误差分布图。图6为TOL算法的定位误差分布图。表1为LLS算法和TOL算法定位误差的比较。

表1 2种算法定位误差的比较
2.2.1 各系统参数对算法定位精度的影响
由图2~图5可以得出以下结论。
1) 采用LLS算法进行水下目标定位时, 在大部分探测区域内, 定位精度较高。随着基线长度的增加, 发射站和接收站两侧区域内的定位精度得到了提高, 但改变的幅度不大。同时, 由于基线长度的增加, 使得基线区域增大, 基线区的定位误差也随之增大(见图2)。
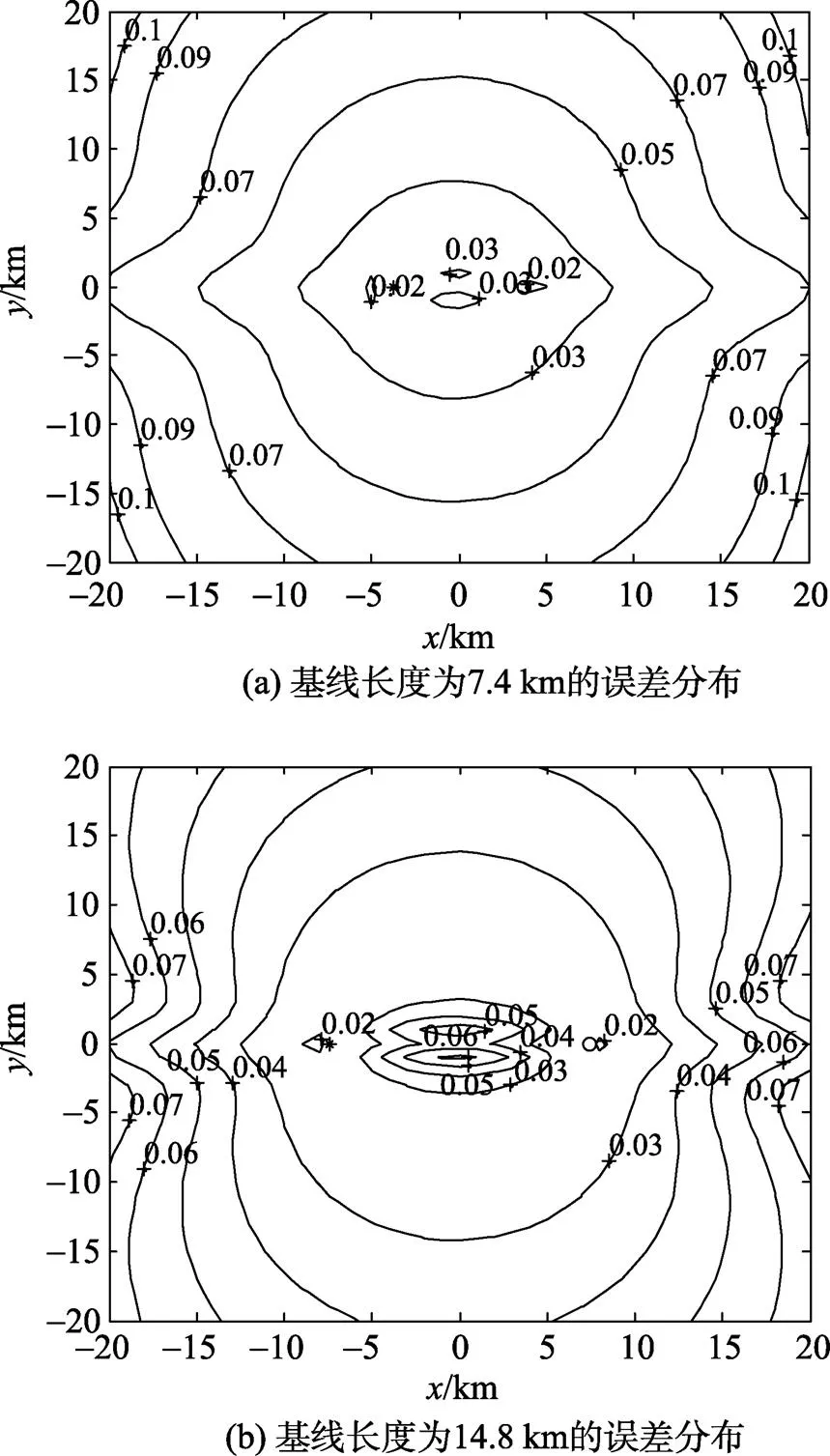
图2 不同基线长度下线性最小二乘定位(LLS)算法定位误差几何分布
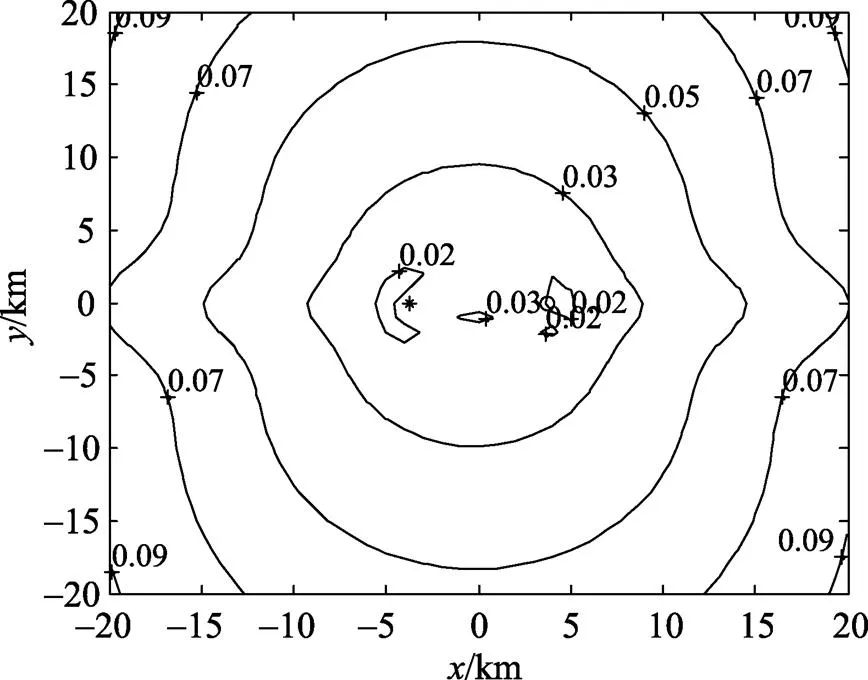
图3 时间测量误差改变时的误差分布

图4 角度测量误差改变时的误差分布

图5 站址测量误差改变时的误差分布
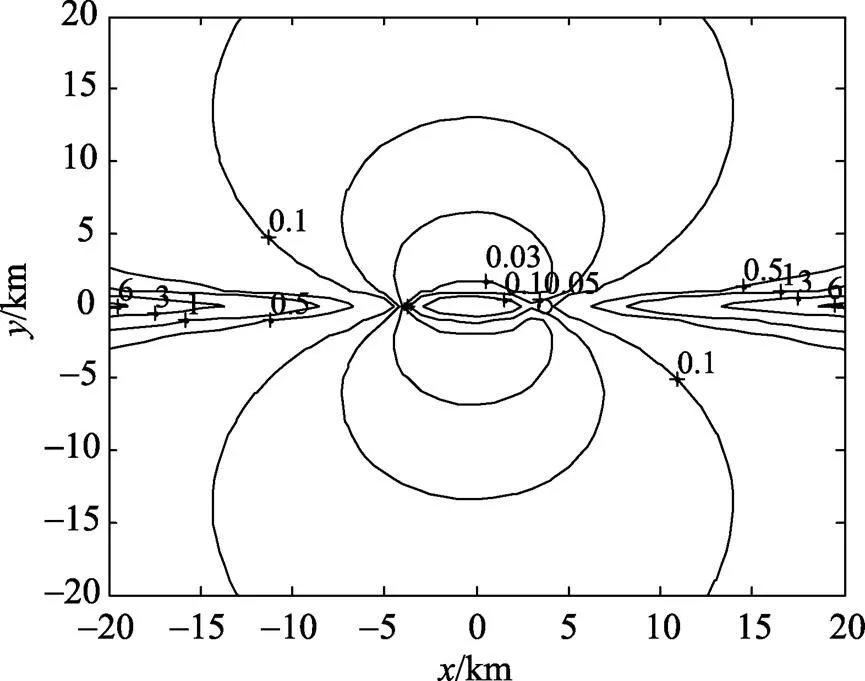
图6 基于波达时间的定位算法(TOL)的定位误差分布
2.2.2 2种定位算法的比较
在对影响算法定位精度的各个因素进行分析后, 为了深入研究LLS算法的定位性能, 特将该算法与双基地TOL算法进行了比较, 从图6和表1的数据可以得出以下结论。
在大部分区域内, 利用LLS算法对目标进行定位时, 系统的定位精度均高于采用TOL算法时的定位精度。在不同的位置, 定位精度的改善程度不同。在基线区和侧边区, TOL算法的定位性能很差, 例如在目标位置为(10, 0) km和(15, 0) km处, 定位误差分别为1 600.1 m和3 848 m, 无法对目标进行定位, 而在相同位置, 采用LLS算法时目标的估计误差仅为34.1 m和51.8 m, 由此可见, LLS算法大大改善了基线区和侧边区的定位性能。在整个探测区域上对所有目标位置点的定位误差求均值, TOL算法为177.2 m, LLS算法为59.8 m, 说明采用LLS算法, 综合利用时间和角度测量信息进行定位, 可以有效提高双基地声纳的定位精度。
3 结束语
[1] Stefano C. Multistatic Sonar Localization[J]. IEEE Journal of Oceanic Engineering, 2006, 31(4): 964-974.
[2] Suhwan K, Bonhwa K, Wooyoung H, et al. Performance Comparison of Target Localization for Active Sonar Sys- tems[J]. IEEE Transaction on Aerospace & Electronic Systems, 2008, 44(4): 1371-1380.
[3] 张小凤. 双/多基地声呐定位及目标特性研究[D]. 西安: 西北工业大学, 2003.
Zhang Xiao-feng. Researches on Localization and Target Property for Bistatic/multistatic Sonar[D]. Xi′an: North- western Ploytechnical University, 2003.
[4] 孙勇, 赵浚渭, 张小凤. 双基地声呐定位算法的研究与比较[J]. 计算机仿真, 2006, 23(9): 129-132.
Sun Yong, Zhao Jun-wei, Zhang Xiao-feng. Research on the Algorithms of Localization Performance of Bistatic Sonar[J]. Computer Simulation, 2006, 23(9): 129-132.
[5] 孙勇, 赵俊渭, 张小凤. 关于双基地声纳定位及其优化算法的研究[J]. 系统仿真学报, 2007, 19 (4): 725-728.
Sun Yong, Zhao Jun-wei, Zhang Xiao-feng. Research on Algorithms of Localization and Opitmal Position Perfor- mance of Bistatic Sonar[J]. Journal of System Simulation, 2007,19 (4): 725-728.
[6] 张小凤, 赵浚渭, 王荣庆, 等. 双基地声纳定位精度和算法研究[J]. 系统仿真学报, 2003, 15(10):1471-1473.
Zhang Xiao-feng, Zhao Jun-wei, Wang Rong-qing, et al. Re- search on Accuracy of Localization Algorithm for Bistatic Sonar[J]. Journal of System Simulation, 2003, 15(10): 1471- 1473.
(责任编辑: 杨力军)
Optimum Localization Algorithm Based on the Linear Least Squares Estimate for Bistatic Sonar
LIURuo-chen, WANG Ying-min, ZHANG Qun
(College of Marine Engineering, Northwestern Ploytechnical University, Xi′an 710072, China)
In the view of the redundant information problem of a bistatic sonar system, an optimal localization algorithm based on the linear least squares estimation is proposed. A mathematical model of underwater positioning is established based on a certain bistatic sonar. Through numerical simulation with the software MATLAB, the effect of the system parameters on localization accuracy is investigated. Also, the algorithm is compared with the time-only-localization (TOL) method. Simulation results show that the proposed algorithm, taking full advantage of the redundant information of the bistatic sonar, can effectively improve the localization accuracy, especially in the neighborhood of baseline and the side area of the bistatic sonar. The algorithm is affected weakly by baseline length and station site error with engineering application. This study may provide a theoretical basis for localization optimization problem of multistatic sonar.
bistatic sonar; linear least squares estimation; localization accuracy; information redundancy
TJ67; O427.9
A
1673-1948(2011)06-0428-05
2011-06-21;
2011-08-16.
刘若辰(1985-), 女, 在读博士, 主要研究领域为水声信号处理.
