模糊综合评判法在学生考试成绩评价中的应用

孙艳，蔡志丹

（长春理工大学 理学院，长春 130022）

目前学生的成绩评价一般采用总分法或平均法，如高考录取采用总分制，学生奖学金的评定采用平均法，以此来衡量学生之间或班级之间的成绩优劣。从评定结果看来，有一定的弊端和不合理性。本文利用模糊综合评判法对学生考试成绩进行评价，因为模糊综合评判是对现实事物本身存在的形态和类属上的亦此亦彼或中介过渡性，从数量上对其归属程度给予刻划和描述，所以具有一定的准确度和可信度。

1 模糊综合评判方法及步骤

模糊综合评判是根据多个因素对一事物进行恰当的评价然后按照某种方法把评价对象的全体排序或选优，或者说，模糊综合评判是针对评价对象的复杂性及其评价指标的模糊性，采用模糊数学的理论与技术，对这种受多种因素影响的复杂的评价对象进行综合评判，从而得到其定量的评价结果的方法。

1.1 确定因素集U

对学生考试成绩采用单因素集评价，即确定每门课试卷评价的要素，在这里用每门试卷中每个类型题目作为一个评判因素。即U={u1,u2,…,un}={1,2,3,…,n} 。

1.2 确定评价等级域V

即确定学生考试成绩评价结果，这里分五级：优秀、良好、中等、及格、不及格、因此V={v1,v2,v3,v4,v5}，v1表示优秀，v2表示良好，v3表示中等，v4表示及格，v5表示不及格。

1.3 建立模糊矩阵

记Ri={ri1,ri2,…,ri5}为单因素评判ui∈U的一个模糊评价，称为因素ui的单因素评价，因此，对几个因素就有几个模糊评价，从而可建立单因素模糊关系评价矩阵

矩阵中rij表示评判对象U中的第i个因素，对应于评价等级V中第 j个元素的隶属关系，即评判某一因素指标属于某一等级的程度。比如：r25表示第二题指标属于不及格的程度，用小于等于1和大于等于0的数字进行刻划。

1.4 建立数学模型

（1）确定评价等级的数值区域

评价等级的划分是作为评判的最终结论，考虑到各因素值以数值形式表示，因此确定相应的数值区域如下：

优秀：[0.90,1]，良好：[0.80,0.90)，中等：[0.70,0.80 ) ，及格：[0.60,0.70)，不及格：[0,0.60)

（2）确定因素权重

（3）统计对各因素的评价结论值

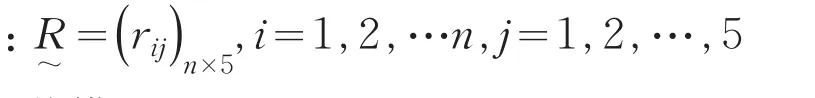
（4）评价模型

2 实例分析

下面就09级光电1班，电信1班，计算机1班，第二学期“高等数学”课程的考试成绩进行综合评判，试卷总分为80分，各试题分数的分配情况如下表

题目序号 一 二 三 四 五 六 七分数 18 18 8 8 10 8 10则因素权重A～=( )0.225,0.225,0.1,0.1,0.125,0.1,0.125

由模型可知，评价因素集U={ }1,2,3,4,5,6,7,评价等级域V={优秀，良好，中等，及格，不及格}。而光电1班，电信1班，计算机1班的评价矩阵分别为：

从而由评价模型计算得评价结果为：

说明：（1）由上述评价结果可以看出，光电1班和电信1班成绩比较正常，但计算机1班成绩偏离较大，这与实际卷面成绩结果相符合。

（2）从评价矩阵还可对三个班不同因素分别进行横向分析比较，比如由评价矩阵第三列元素可以看出学生对第三题的回答普遍不好，由此可以提醒教师在教学过程中注意这方面的教学。

（3）从评价结果看，计算机1班不及格的学生明显高于另外两个班，通过调查发现，计算机1班学生的入学基础要弱于另两个班，另外，光电1班和电信1班的授课教师是任教十余年的中年教师，而计算机1班是由刚刚走上讲台的年轻教师授课。这也说明在强调学生主动学习的同时，要加强提高授课教师的业务水平和授课效果。

［1］杨纶标，高英仪.模糊数学原理及应用［M］.广州：华南理工大学出版社，2006.

［2］杨云，任建军.模糊多属性决策在装备质量评价中的应用［J］.数学的实践与认识，2005，35（3）：34-38.

［3］陈伟.模糊数学在数学建模中的应用［J］.数学的实践与认识，2005，35（4）：1-5.