基于分枝模态法的面对称布局飞行器结构动力学建模

史晓鸣,许 泉,杨炳渊,唐国安

(1.复旦大学 力学与工程科学系,上海 200433;2.上海机电工程研究所,上海 200233)

0 引言

对大型复杂的多自由度结构,虽可整体建立有限元模型,直接进行动力学分析,但模型的单元数和自由度数常多达数十万甚至数百万,需要很大的计算规模和机时。特别是颤振等耦合动力学问题,由于气动矩阵的非稀疏性和非对称性,计算规模和机时更是令人难以容忍。采用动态子结构方法是解决此类问题的有效途径[1～5]。20世纪60年代,国外对将部件模态引入整体的动力学分析进行了研究[6]。文献[7]提出了分枝模态法,对复杂结构的各部件施加一定的约束,使其局部刚化,形成各个分枝系统,并确保各分枝的运动型态组合能表征整体结构的运动型态[7]。此后,文献[8～11]等先后提出并改进了约束界面和自由界面的模态综合法。文献[12]用模态坐标表达约束界面的位移,发展了约束界面模态综合法。文献[13]对自由界面模态综合法作了改进,发展了双协调动态子结构法。

分枝模态法在工程实践中应用较多,其分枝变形不重迭原则使模态刚度矩阵解耦,但模态质量矩阵在分枝间一般仍存在惯性耦合。本文利用整体有限元模型计算面对称布局飞行器固有模态,根据整体模态具对称或反对称特征,按对称和反对称模态划分分枝,用分枝模态法建立的结构运动方程在不同分枝间也可实现惯性解耦,这利于问题的简化,以及自由度和计算规模的缩小。为此,本文对基于分枝模态法的面对称布局飞行器结构动力学建模进行了研究。

1 飞行器模态分析

设飞行器外形如图1所示。其中：机身、机翼、垂尾组成面对称布局,机身、机翼和垂尾均为有纵向和横向加劲的半硬壳式结构。机身内部除结构件外,还安装仪器设备、贮箱、发动机和有效载荷等非结构质量。

图1 飞行器外形Fig.1 Vehicle conf iguration

1.1 飞行器有限元建模及模态计算

根据飞行器的结构特点,用MSC.Patran软件建立飞行器整体的有限元模型。其中：半硬壳式结构用壳单元与梁单元混合建模,蒙皮部分用6自由度的壳单元模拟,桁条、翼肋和隔框等加劲部分用相同自由度的梁单元模拟。非结构质量则建立点质量单元,通过多点约束(MPC)分散固定在对应弹身舱段的结点上,量值和位置由杠杆原理算得。

用MSC.Nastran软件的求解器解广义特征值问题

即可得到固有模态。此处：k,m为结构的刚度和质量阵;ω2为系统特征值;φ为系统特征向量。

1.2 模态结果分析

飞行器的固有模态计算结果见表1。其中振型形态主要有关于机身垂直子午面对称、关于机身垂直子午面反对称和垂尾变形为主的三种(如图2～4所示)。可发现：对称振型中两片机翼作关于机身垂直子午面对称的垂向振动,机身作垂向弯曲振动,且两者耦合程度很高,无显著的纯机身或纯机翼的振动模态,而垂尾基本无垂直于垂尾平面的侧向振动,只随机身的振动作垂直方向的刚体运动;反对称振型中两片机翼作关于机身垂直子午面反对称的垂向振动,机身作绕纵轴的扭转振动,两者耦合程度也很高,垂尾除随机身扭转作垂直于垂尾平面的刚体侧向振动外,还存在一定的侧向弹性振动;垂尾变形为主的振型中垂尾作垂直于垂尾平面的侧向弹性振动,机身和机翼只有量级很小的局部振动。此外,仅在频率86 Hz以上出现机身侧向弯曲为主的侧弯一阶振型,低阶模态中无明显的机身或机翼侧向弯曲。

表1 固有模态Tab.1 Natural modal

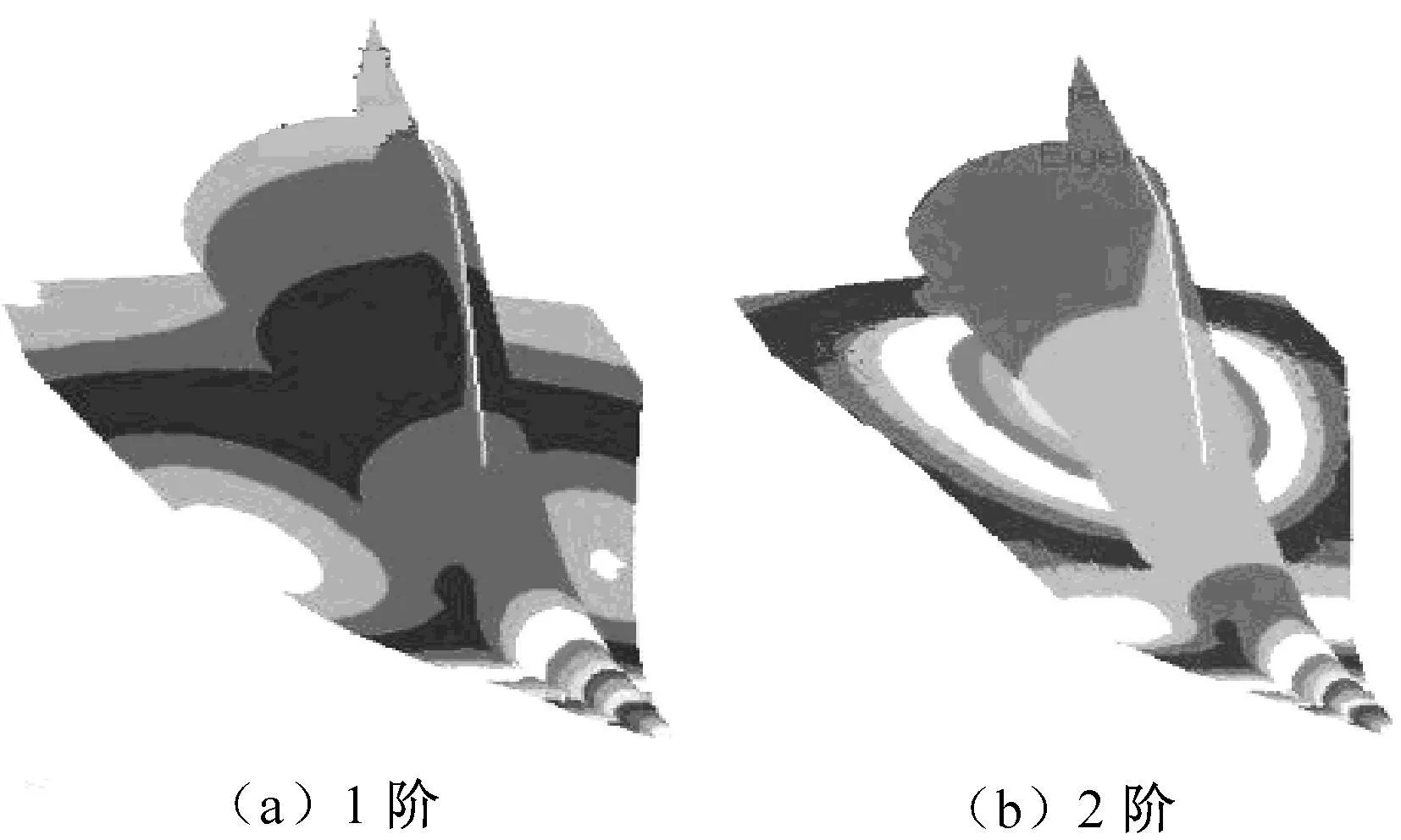
图2 对称振型形态振型Fig.2 Symmetrical mode shape

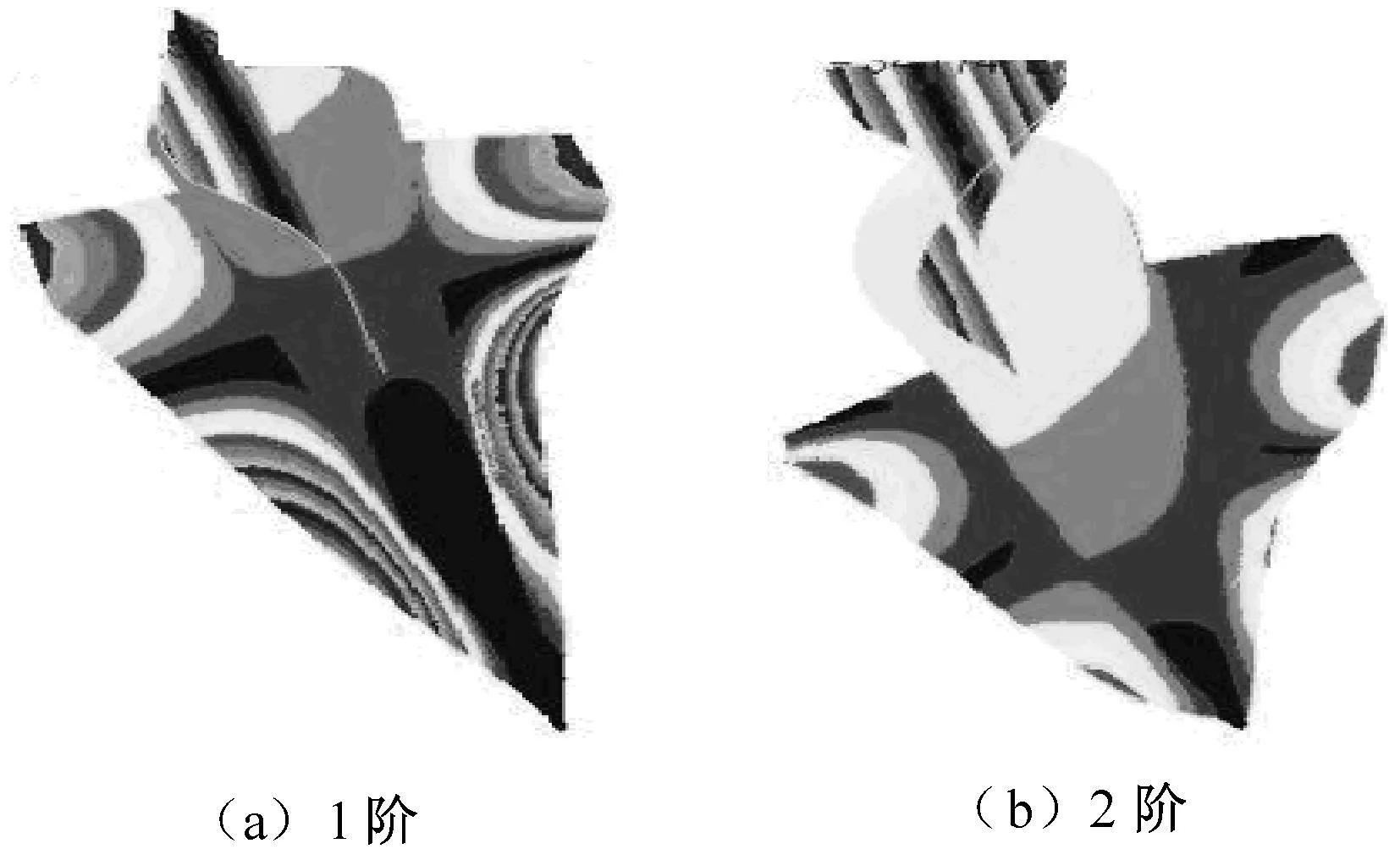
图3 反对称振型形态振型Fig.3 Antisymmetrical mode shape

图4 垂尾振型形态振型Fig.4 Vertical tail mode shape

2 分枝模态法建模

采用分枝模态法建模。对本文的飞行器构型,传统方法是按自然结构部件划分分枝,如文献[2、3]划分为机身、机翼和尾翼三个分枝。但本文飞行器的机翼和机身融为一体,对将机翼刚化形成的机身分枝或将机身约束形成的机翼分枝,获取分枝模态的试验或计算均较难。另外,机翼机身间静不定的连接,模态综合时要求考虑约束模态,计算繁琐且增加多个自由度[14]。根据上述模态分析结果面对称飞行器对称反对称振型的特征,本文的分枝划分除在垂尾与机身的结合部仍将机身约束形成垂尾分枝外,对融为一体的机身机翼部分不按自然部件划分为机身和机翼两个分枝,而按对称和反对称振型划分分枝。这样不但克服了上述缺点,分枝模态的获取简单易行,而且由于对称和反对称振型属于同一结构组成的主模态,两个分枝间也实现了惯性解耦。

2.1 分枝划分

根据上述考虑,按分枝模态法分枝变形不重迭原则,全机可分为三个分枝。

a)机身机翼对称振型分枝：包括简化为自由梁的机身在xoz平面内的弯曲振动、简化为平板的两片机翼关于xoz平面对称的弹性振动,以及全机的刚体沉浮、俯仰运动。垂尾作为刚体附连在机身上随机身运动。

b)机身机翼反对称振型分枝：包括简化为扭转轴的机身绕ox轴的扭转、简化为平板的两片机翼关于xoz平面反对称的弹性振动,以及全机刚体侧移、偏航和滚转运动。垂尾作为刚体附连在机身上随机身扭转作牵连运动。

c)垂尾分枝：垂尾简化为弹性平板固定于不动的机身轴线上。

在这三个分枝中,未考虑机身在xoy平面内的侧向弹性振动。这是因为两片机翼与机身融为一体,机身在侧向的刚度很大,侧向振动模态的频率很高(大于表1中所有的频率),在全机的低频段上几乎不存在侧向的弹性变形。

2.2 结构运动方程

根据三个分枝的划分,飞行器结构物理坐标下的运动可表示为三个分枝模态振型的叠加,有

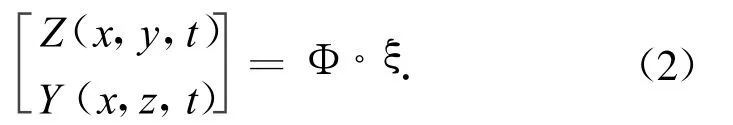
式中：t为时间;

ξ为全机结构模态坐标矢量,且

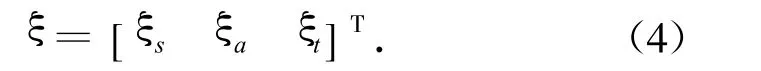
此处：Φs,Φa,Φt分别为由机身机翼对称振型分枝ns个模态、机身机翼反对称振型分枝na个模态和垂尾分枝nt个模态振型函数组成的矩阵;上标(z)、(y)分别表示垂向振动和侧向振动。

忽略工程中常见的小阻尼影响,由拉格朗日方程可导出结构的运动微分方程为

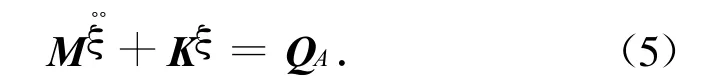
式中：M,K分别为结构的模态质量和模态刚度阵;QA为广义力矢量,由各分枝对应的分量Qs,Qa,Qt构成。设作用于飞行器表面单位面积dσ的载荷为Δp,则

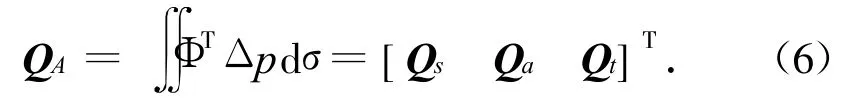
2.3 运动方程解耦

模态质量阵可表示为

式中：m(x,y,z)是局部质量密度函数;Φ(x,y,z)为振型函数;d V为局部单元体积。

将模态质量矩阵按三个分枝分块,有

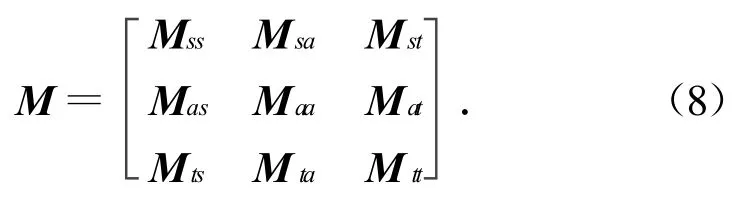
式中：下标s,a,t分别表示机身机翼对称振型分枝、机身机翼反对称振型分枝和垂尾分枝模态对应的行和列。

同一分枝内的固有模态对质量具加权正交性,故子矩阵Mss,Maa,Mtt均为对角线阵,可由各分枝结构的模态计算或模态试验获得。

机身机翼对称振型分枝和机身机翼反对称振型分枝同属机身机翼结构的主模态,它们之间也满足正交性条件,交叉项的模态质量矩阵为零矩阵。即

垂尾分枝模态振型在机身机翼物理坐标z向的数值为零,而机身机翼对称振型分枝在垂尾物理坐标y向的数值也为零,故有关机身机翼对称振型分枝和垂尾分枝交叉项模态质量阵为零矩阵,即

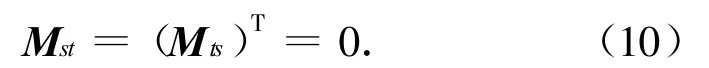
机身机翼反对称振型分枝在垂尾物理坐标上的数值不为零,故机身机翼反对称振型分枝与垂尾分枝间存在惯性耦合,即

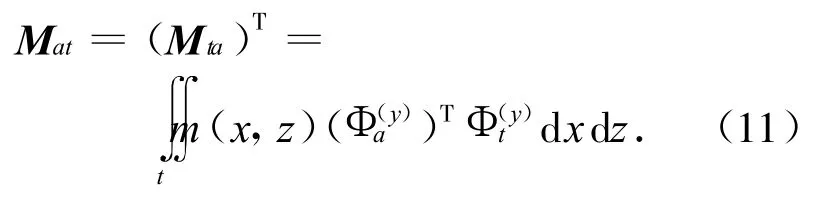
则模态质量矩阵可表示为

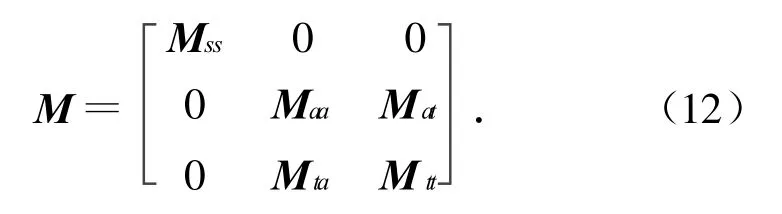
由于分枝的选择满足变形不重迭原则,故模态刚度阵为一无刚度耦合的对角阵,即

式中：Kss,Kaa,Ktt为各分枝的模态刚度阵,可由各分枝结构的模态计算或模态试验获得。

对一般的动力响应问题,如发动机脉动、突风、分离、姿控喷流等响应,载荷Δp=Δp(t)只是时间的函数,由式(6)表示的广义力矢量对应各分枝的分量互相独立,结构运动微分方程式(5)可分为两组互相独立的微分方程

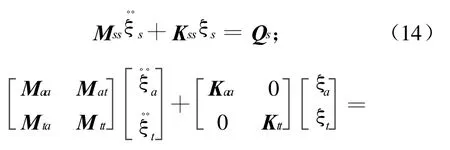
对颤振、伺服气弹等运动稳定性问题,广义力矢量是与运动有关的参数,则

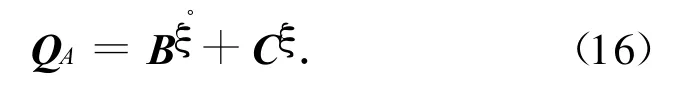
式中：

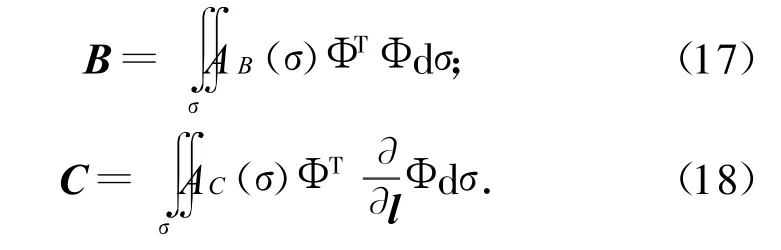
此处：AB(σ),AC(σ)为与流场相关的参数;σ为飞行器表面任意点;l为气流方向。

同样可将B,C如式(8)按三个分枝分为3×3块。因固有模态对气动力不具加权正交性,故此处的对角线子矩阵是非对角线阵,且C为非对称阵。但机身机翼对称和反对称振型分枝的交叉项因对机身和左右两片机翼积分之和为零,仍有

由于垂尾分枝模态在机身物理坐标上的位移为零,机身机翼对称振型分枝在垂尾侧向坐标上的位移为零,故

因此,B,C也有与式(12)的M相同的形式,即

由此,对颤振、伺服气弹等运动稳定性问题,结构运动微分方程式(5)同样可转化为式(14)、(15)表示的两组互相独立的运动微分方程。

3 验证

为验证本文分枝模态法的建模精度,对图1所示飞行器,按划分的三个分枝分别建立有限元模型计算得到三个分枝的模态参数,取机翼机身对称振型分枝、机翼机身反对称振型分枝和垂尾分枝前3阶或4阶模态,建立式(14)、(15)的分枝模态法运动方程,令方程右端广义力矢量为零,计算其固有频率和振型,并与本文按飞行器整体建立有限元模型的计算结果进行比较。固有频率的计算结果见表2、3。由表可知：除个别阶序偏差稍大外,多数模态阶序的偏差小于5%,精度满足工程设计要求,同时振差异亦很小,因篇幅所限文中未列出。

表2 直接法与分枝模态法计算固有频率比较(对称分枝)Tab.2 Some frequencies results by direct and branch mode method(symmetry branch)

表3 直接法与分枝模态法计算固有频率比较(反对称与垂尾分枝)Tab.3 Some frequencies results by direct and branch mode method(antisymmetry&vertical tail branches)

4 结束语

本文根据面对称布局飞行器模态振型的特征,按对称和反对称形态划分分枝,建立分枝模态法结构动力学模型。通过理论推导获得只有机身机翼反对称振型分枝与垂尾分枝存在惯性耦合,而对称振型分枝不与垂尾分枝耦合,由此得到对部分分枝解耦的两组互相独立的运动微分方程。本文方法对大型复杂多自由度的面对称布局飞行器结构的动力响应分析和气动弹性稳定性分析有一定的参考价值,可用于减缩自由度和计算规模。

[1]吴兴世,王文亮.弹性飞机舱内噪声分析的双协调动态子结构法[J].力学学报,1987,19(增)：127-131.

[2]杨炳渊.全弹组合体超音速颤振的一种工程计算方法[J].空气动力学学报,1983,3(4)：99-105.

[3]杨炳渊,樊则文.弹性飞行器气动伺服弹性耦合动力学仿真[J].宇航学报,2009,30(1)：134-138.

[4]恽伟君,朱农时,段根宝.多重动态子结构法在大型复杂结构动态计算中的应用[J].振动与冲击,1987,(1)：13-23.

[5]邱吉宝,王建民,谭志勇.运载火箭结构动力分析的一些新技术(第二部分)：运载火箭结构动力学分析)[J].导弹与航天运载技术,2001(4)：16-21.

[6]王文亮.结构振动与动态子结构方法[M].上海：复旦大学出版社,1985.

[7]GLADWELL G.M L.Branch mode analysis of vibrating system[J].Journal of Sound and Vibration,1964,1(1)：41.

[8]HURTY W C.Vibration of structure systems by component mode synthesis[J].Journal Engreering Mech Div,ASCE,1960,86：51-59.

[9]CRAIG R R,BAM PTON M C C.Coupling of substructures for dynamic analysis[J].AIAA Journal,1968,6：1313-1319.

[10]HOU S N.Review of modal synthesis techniques and a new approach[J].Shock and Vibration Bulletin,1969,40(4)：25-39.

[11]RUBIN S.Improved component-mode representation for structural dynamic analysis[J].AIAA Journal,1975,13：995-1006.

[12]胡海昌.很多自由度体系的固有振动问题(约束模态法)[J].航空学报,1980(2)：28-36.

[13]王文亮,杜作润,陈康元.模态综合技术短评和一种新的改进[J].航空学报,1979(3)：32-51.

[14]王文亮.惯性耦合法述评及其一般原理[J].上海力学,1982,2(1)：1-10.