某大结构变化空间飞行器转动惯量在轨估计

李广兴,肖余之

(上海宇航系统工程研究所,上海 201108)

0 引言

随着航天技术的不断发展,空间飞行器的结构越来越复杂,任务越来越多,对控制精度的要求越来越高。结构的复杂性表现为飞行器常有大挠性太阳帆板、大挠性天线和各种有效载荷;任务的多样性导致飞行器的结构经常发生改变,如飞行器载荷释放、卫星回收、空间站与载人飞船或货运飞船对接等任务。姿态和轨道控制系统是保证任务成功的一个重要子系统,任务的复杂性和多样性要求控制算法不作较大的改变就能适应大范围的转动惯量、质心和质量等质量特性参数的变化,因此需要这些参数的信息已知,而通常飞行器在轨结构的改变造成这些参数均为未知。

对空间飞行器质量特性参数的估计技术进行了大量研究。文献[1]基于推力器建立了动力学模型,将转动惯量各分量的逆和质心作为待估变量,以陀螺为测量传感器,应用二阶滤波器进行估计;文献[2]基于控制力矩陀螺的动力学模型,以速率陀螺和加速度计为测量传感器,对转动惯量、质心和质量进行估计,并利用空间站的数据进行仿真;文献[3]通过航天器机动建立转动惯量与角动量间的关系,用最小二乘法进行估计,并通过在轨数据验证算法;文献[4]用角动量守恒确定Cassini航天器的转动惯量;文献[5]基于满足欧拉方程的方法估计动力学参数;文献[6]总结了质量特性参数在轨估计算法,并于2006～2008年间在空间站上进行了质量特性估计试验。上述研究中多数算法均基于推力器为执行机构,量测量一般为星体角速度和加速度,估计方法有最小二乘法和卡尔曼滤波法,估计精度一般为相对误差小于5%。本文针对某空间飞行器转动惯量变化大的特点,对其转动惯量的在轨估计技术进行了研究。

1 动力学方程

基于推力器执行机构,空间飞行器挠性动力学方程可表示为

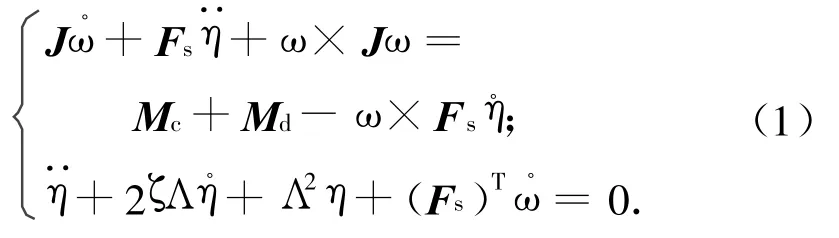
式中：J,ω分别为空间飞行器的转动惯量阵和角速度;Mc为控制力矩;Md为干扰力矩;Fs为空间飞行器与太阳电池阵的耦合系数阵;ζ为太阳电池阵阻尼系数阵;Λ为太阳电池阵模态频率阵;η为太阳电池阵模态坐标矢量。

2 基于推力器的转动惯量估计算法

因惯量积远小于主惯量,其估计值易被噪声淹没,且姿态控制算法的设计主要取决于主惯量值,故惯量积无需估计。

忽略挠性振动,刚体的动力学方程可表示为

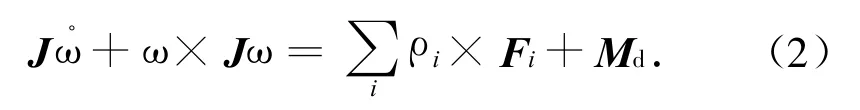
式中：ρi为第i个推力器的作用点相对质心坐标系的位置矢量;Fi为第i个推力器的推力;J为空间飞行器的主惯量阵,且J=diag[JxJyJz]。式(2)两边同乘ωT,得

整理后有

与推力矩相比,环境力矩很小,Md可忽略,则式(4)变为

本文以X轴为例,讨论Jx的估计方法。

估计原理：选择合适推力器工作,使滚动角速度ωx发生某种变化,而其他两轴的角速度ωy,ωz为小量,通过测量滚动角速度并综合动力学方程估计滚动轴的惯量。

选择的推力器如图1所示。图中：

a)本体坐标系Ob-XbYbZb,Ob为推力器的质心位置。

b)布局坐标系Os-XsYsZs,与星体固联,Os为星箭分离面几何中心;OsZs轴在星箭分离面内,垂直指向星体对地面;OsXs轴垂直于星箭分离面,指向有效载荷舱;O s Y s轴与O s Z s、O s X s轴构成右手坐标系。

推力器Th1、Th2提供+OXb轴的控制力矩,Th3、Th4提供-OXb轴的控制力矩。

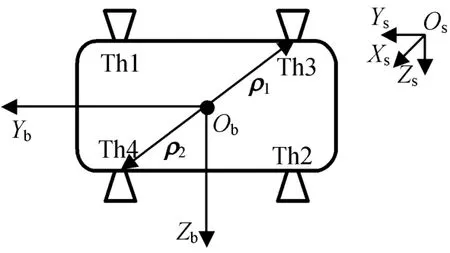
图1 X轴推力器选择Fig.1 Thrusters choice for roll axis

当推力器Th1、Th2工作时,有

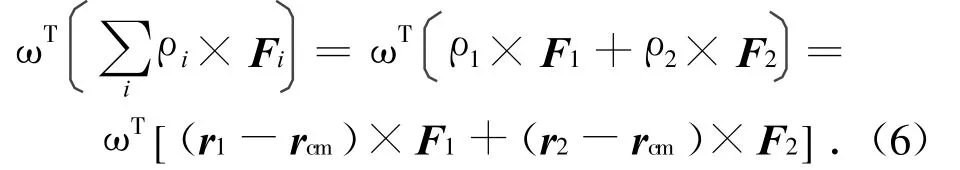
式中：ri,rcm分别为第i个推力器和质心在Os-XsYsZs系中的坐标。因F2=-F1,式(6)变为

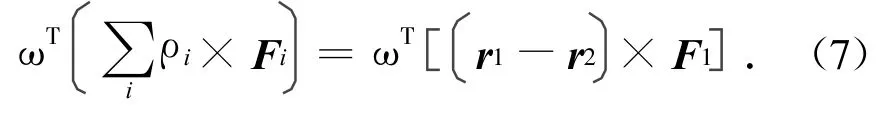
同理,当推力器Th3、Th4工作时,可得

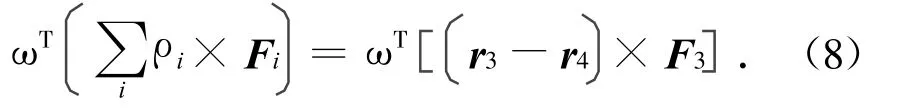
定义变量

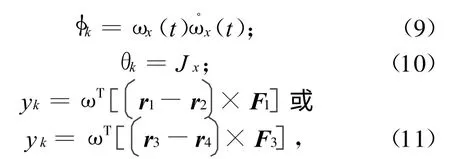
则有

式中：vk为测量噪声,且。

令性能指标函数

可得令Jf最小的估值

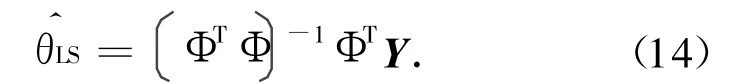
式中：N为数据采样数;Φ=[φ1φ2… φN]T;Y=[y1y2… yN]T。

a)Φ求取

Φ是由φk即构成的列阵。ωx(t)可测,但不可测,分析ωx(t)是否能通过姿态确定系统获得。

根据先验信息可得Jx=800 kg◦m2,r1=[2 120 970 -350]Tmm,F1=TN,r2=[2 120 -970 350]Tmm,由式(5)、(7)可算得

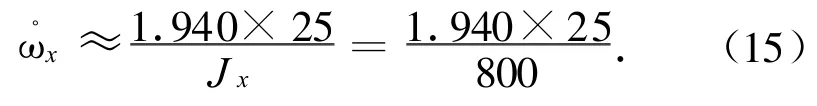
对式(15)进行积分,得

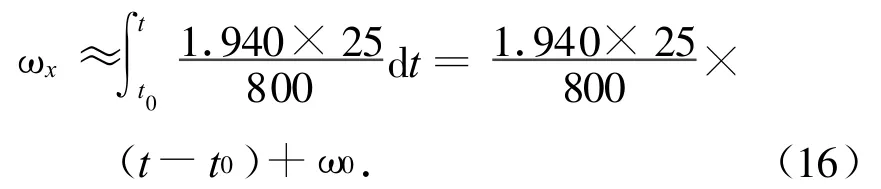
选择t-t0=0.4 s,初始ω0很小,则ωx≈1.39(°)/s。推力器工作时,1个姿控周期T内姿态角速度较大,星敏感器不可用,此时陀螺的角速度的估值不可由姿态确定系统获得。由陀螺的测量模型,得

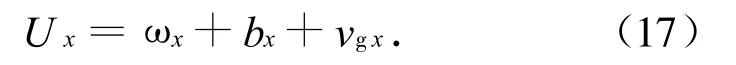
式中：Ux为测量的滚动角速度;ωx为真实滚动角速度;bx为常值漂移;vgx为测量噪声。陀螺的角速度的估值

b)推力器喷气逻辑设计

为满足姿态角速度不大于2(°)/s的要求,由式(16)可得

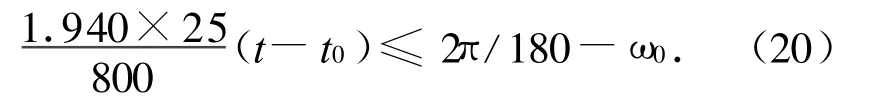
推力器工作起始工作时刻,ω0很小可忽略,则

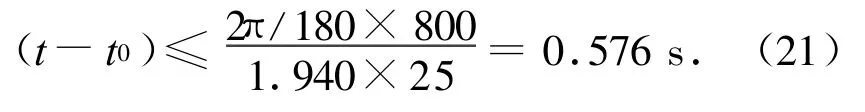
推力器只能在0.576 s内工作,否则陀螺输出将会饱和。如2台推力器满喷,推力器只能工作1个控制周期,但仅使用1个控制周期的数据难以对Jx进行有效估计,因此需对推力器的指令喷气时间进行设计,并要求不超出陀螺2(°)/s测量范围。

为能获得足够的数据以估计Jx,且Φ中的数据会有较大的跳变以增大能观度,同时角速度应满足约束,推力器的指令喷气时间设计如下。

由式(15),可得

仿真时间为t1-t0=0.8 s,t2-t1=0.4 s,t3-t2=0.8 s。每台推力器在每个控制周期内开启时间

则可得

因此,本文仿真时间和式(23)的选择合理,角速度满足小于2(°)/s的约束。

c)yk求取

式(11)表明：yk由角速度,推力器作用点在Os-XsYsZs系中的坐标和推力值经运算获得;姿态角速度可测;推力作用点在Os-XsYsZs系中的的坐标已知;推力大小可在轨进行标定,故yk可得。本文取推力器的标称推力值。

Jx的估算流程如图2所示。

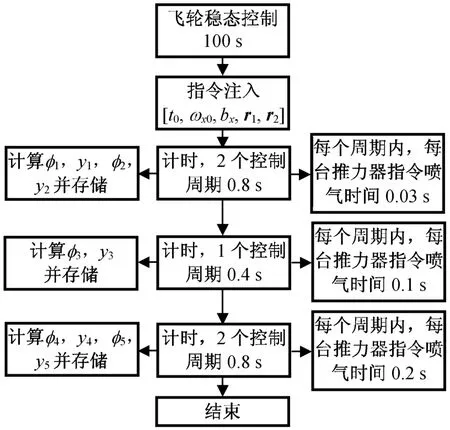
图2 估计算法流程Fig.2 Flowchart of estimated algorithm

步骤a)给出推力器开始工作指令,输入初值t0,ωx0,bx,r1,r2;

步骤e)获得5组数据,用式(14)求出X轴转动惯量的估值。

3 仿真

仿真初始条件见表1。设飞轮稳态控制100 s后,推力器开始工作。仿真结果如图3～6所示。同样初始条件下的5次估计结果见表2。

5次仿真的结果表明：估值与真值的相对误差小于5%,姿态角小于1.5°,姿态角速度满足2(°)/s的约束要求,燃料消耗仅约11 g,且不会激起挠性振动。

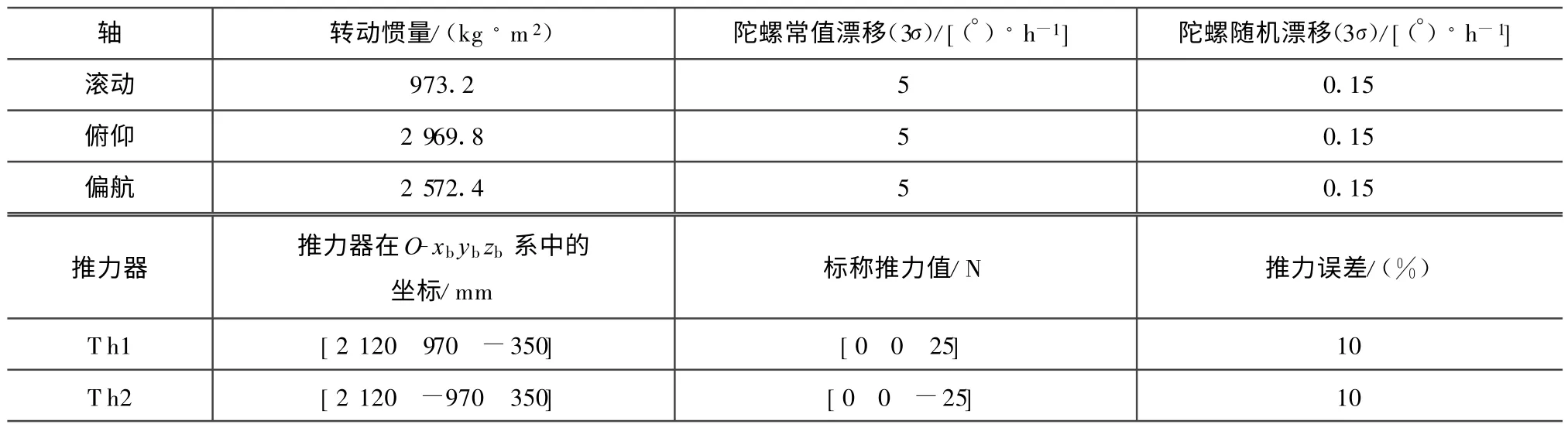
表1 初始条件Tab.1 Initial condition

图3 欧拉角Fig.3 Euler angle

图4 欧拉角速度Fig.4 Euler angular velocity

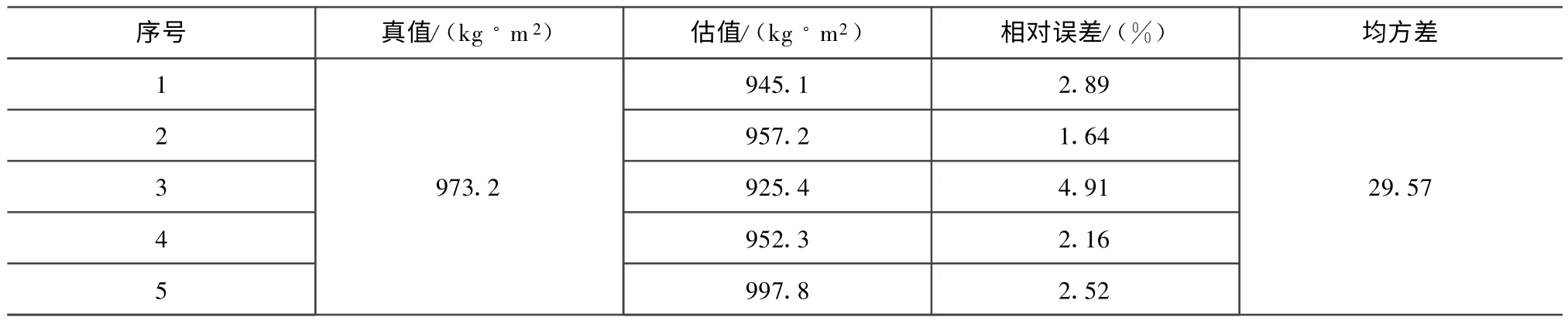
表2 估计结果Tab.2 Estimated results

图5 控制力矩Fig.5 Control moment

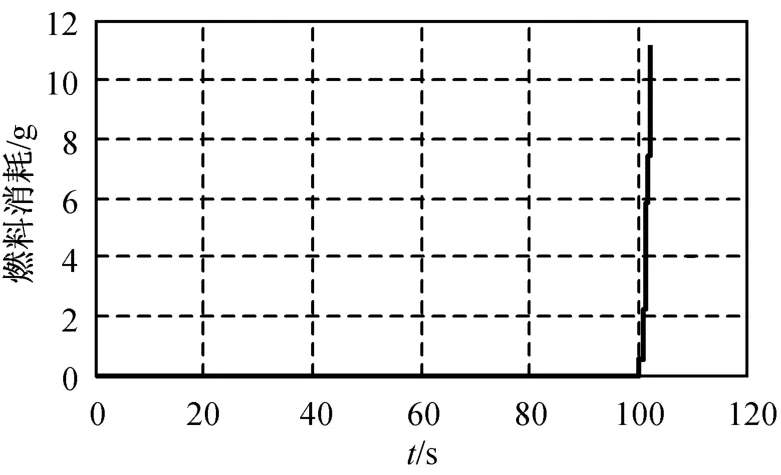
图6 燃料消耗Fig.6 Consuming fuel

4 结束语

本文研究了某空间飞行器转动惯量的在轨估计方法。选择合适的推力器,设计指令喷气时间,通过姿态角速度的测量值获得量测,用最小二乘方法估计转动惯量。仿真结果表明估计精度可达相对误差小于5%。该估计算法简单,计算量小,燃料消耗小,较适于工程应用。此外,本文算法依据刚体动力学模型获得,但仿真中加入了挠性模型,故对挠性航天器有适用性。

[1]BERGMANN E.V.Mass property estimation for control of asymmetrical satellites[J].Journal Guidance,1987,10(5)：483-491.

[2]BERGMANN E.Spacecraft mass property identification with torque-generating control[J].Journal Guidance,1990,13(1)：99-103.

[3]TANYGIN S,WILLIAMS T.Mass property estimation using coasting maneuvers[J].Journal of Guidance Control,and Dynamics,1997,20(4)：625-632.

[4]LEE A Y,WERTZ J A.In-flight estimation of the cassini spacecraft's inertia tensor[J].Journal of Spacecraf t and Rockets,2001,39(1)：153-155.

[5]MARK P.Estimation of a spacecraft's attitude dynamics parameters by using f light data[J].Journal of Guidance Control,and Dynamics,2005,28(4)：594-603.

[6]WILSON E,SUTTER D.Motion-based mass-and thruster-property identification for thruster-controlled spacecraft[C]//Proceedings of the 2005 AIAA Aerospace Conference.Arlington：AIAA,2005：1-39.