滑模变结构控制在电动舵机上的应用研究

赵 峰,顾鹏程,赵宇宏

(1.中国人民解放军驻上海航天技术基础研究所军事代表室,上海 201109;2.上海航天控制技术研究所,上海 200233;3.总装备部南京军事代表局驻上海地区军事代表室,上海 201109)

0 引言

飞行过程中,导弹的多个结构参数会发生剧烈变化。其中,电动舵机作为导弹飞行控制系统的执行机构,其时间常数和传递系数将随舵面铰链力矩和外加干扰力矩而变。参数的改变会影响整个系统的动态性能,甚至危及系统稳定性,因此要求控制系统有较好的抗干扰能力和鲁棒性[1]。传统PID控制算法由于环境适应性和抗负载能力等的不足,不能很好满足电动舵机的控制需求。对非线性系统或参数时变线性系统来说,变结构控制方法是一种有效控制方法,它具有对负载扰动鲁棒性优、对系统参数不敏感、动态响应快等优点。对高动态电动舵机,变结构控制成为一种较佳的选择。为此,本文对滑模变结构在电动舵机上的应用进行了研究。

1 控制对象模型

设导弹电动舵机系统结构如图1所示,其中电机一般采用直流伺服电机。根据永磁直流伺服电机工作特性,不考虑舵面铰链力矩、外加干扰力矩和摩擦力矩时,其输入电压到电机输出转速的传递函数

式中：Km,τm,τe分别为电机的传递系数、机械时间常数和电气时间常数,且Km=1/ke。此处：ke为电机电势常数。实际中由于τe≤τm,式(1)可简化为

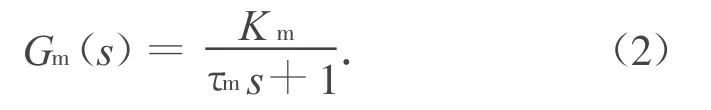
同时考虑电机输出至舵偏角的传递函数,最终可得控制对象的传递函数

式中：K=(keki)-1;S为拉氏算子。此处：ki为传动机构减速比。

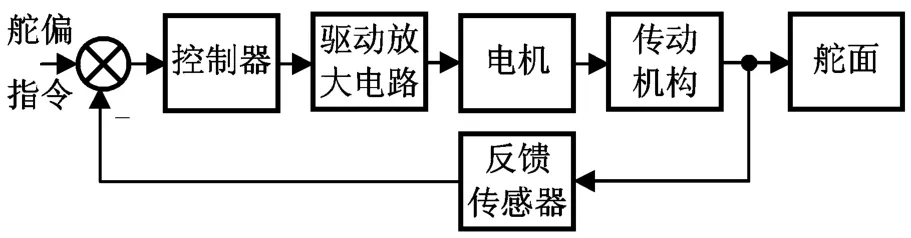
图1 电动舵机结构Fig.1 Structure of electromechanical actuator

2 滑模变结构控制器设计

2.1 切换面设计

式(3)所示的电动舵机模型可表示成微分形式

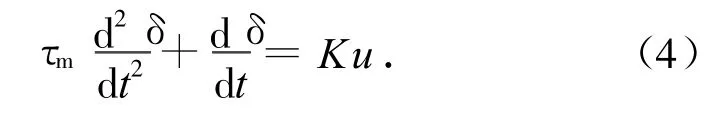
考虑舵机系统是一个位置跟随系统,要求系统输出位置跟踪复现输入,故取舵偏指令角ui与实际舵偏反馈信号的误差信号ue及其一阶导数为状态变量,即。则式(4)可写成

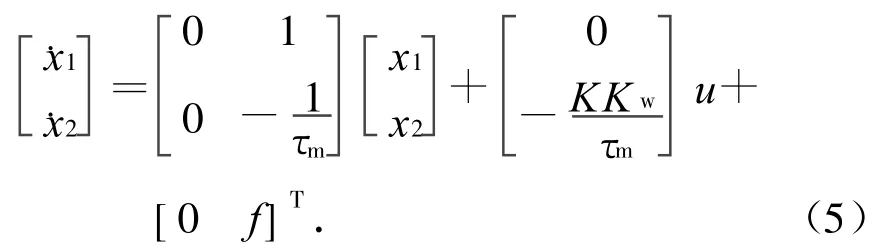
取切换函数

式中：c为滑模线斜率。

2.2 趋近律选择

采用滑模控制时,为提高控制品质需引入趋近律,主要原因是：

a)减少能动阶段时间。滑模运动的可达性仅实现了状态空间任意位置的运动点必于有限时间内到达切换面,但此段时间的具体轨迹未作规定。为改善该段运动的运动品质,一定程度上可用趋近律进行控制。

b)减小抖振。从物理意义上理解,产生抖振的原因是系统运动以其固有的惯性冲向切换面时具有有限大的速度。因此,可为控制该速度而设计各种趋近率。

常用的趋近律有等速趋近律、指数趋近律和幂次趋近律等。其中,指数趋近律的形式为

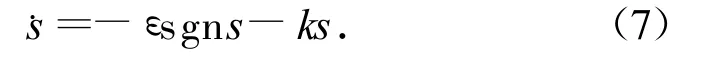
将控制对象状态方程式(5)和切换函数方程式(6)代入趋近律方程式(7),即可得基于指数趋近律的控制输出方程

式中：a1=1/τm;k0=KKw/τm[3]。

2.3 抖振改善

对控制方程式(8),由于含不连续的符号函数sgn s,使滑动模态呈现抖动形式。这种不期望的高频抖动可能会激发系统的未建模动态,影响控制性能,严重时还会导致系统不稳定。为降低抖动的影响,本文用连续函数代替τm[4]。此处：ξ为误差e的函数,有

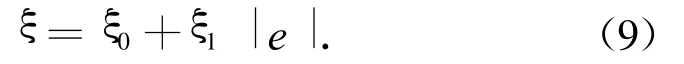
其中：ξ0,ξ1为正的常数。选择一个合适的sξ,可显著降低抖动。本文系统采用连续函数时,阶跃指令0.1 V的符号函数连续化前后的相轨迹如图2所示。由图可见：抖振获得了较大改善。

由此,最终可得系统控制结构如图3所示。

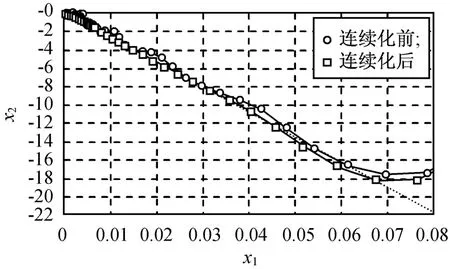
图2 符号函数连续化前后系统相轨迹Fig.2 State traceof system fore-and-af ter sign function continuouing

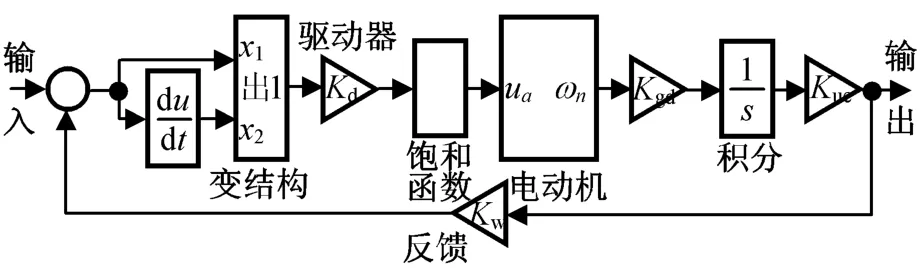
图3 电动舵机滑模变结构控制模型Fig.3 Model of electromechanical actuator using sliding mode variable structure

3 仿真

根据实际电动舵机参数,取变结构控制参数为：c=150,k=600,ε=1100,ξ0=1,ξ1=8。在舵系统空载加载及参数摄动条件下进行仿真,同时将变结构控制算法与传统PID算法进行了对比,以检验所设计的变结构算法在加载和参数变化条件下的鲁棒性和抗干扰性,其中PID的控制方程为

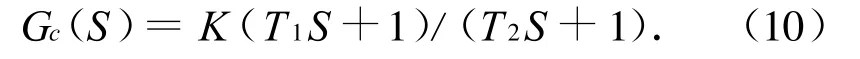
式中：T1=0.015;T2=0.004;K=100。

3.1 快速性

比较滑模变结构(VSS)控制算法和传统PID控制算法的舵系统快速性,在空载条件下分别加入不同幅值的阶跃指令,响应结果分别如图4、5所示,试验结果见表1。

图4 空载5 V阶跃响应Fig.4 5 V step response without load

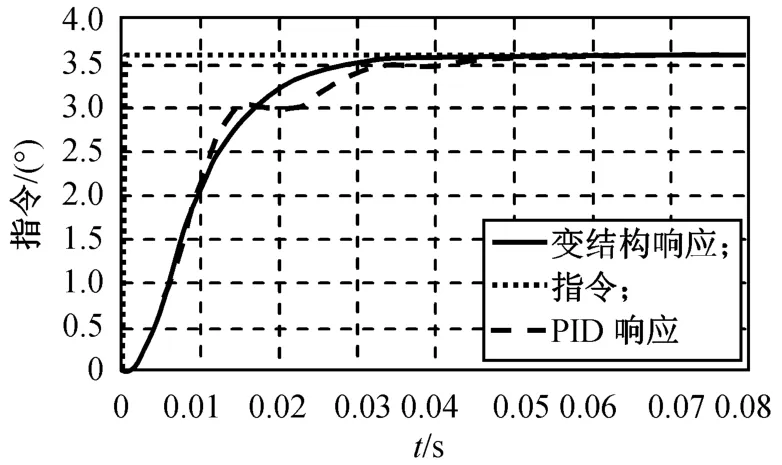
图5 空载单位阶跃响应Fig.5 Contrast of unit step response without load

由表1可知：VSS控制算法的快速性(如上升时间、调节时间)较传统PID控制算法有明显提高,指令越小,优势越明显。

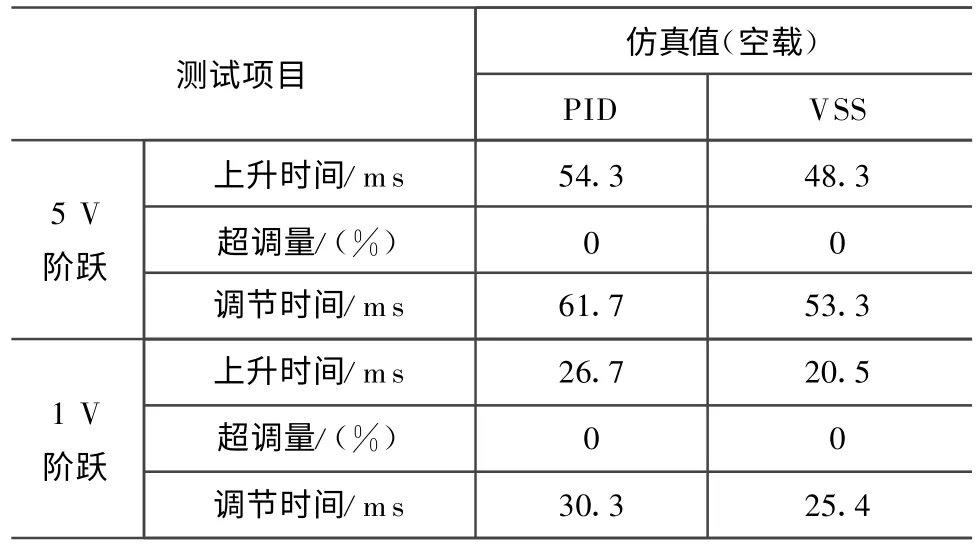
表1 空载单位阶跃响应对比结果Tab.1 Results of unit step response without load

3.2 抗负载能力

由于整体上,铰链力矩与舵偏角成比例关系,同时考虑舵机工作在相对恶劣(铰链力矩系数较大)条件下,在舵机上加入弹性负载10 N◦m/(°),指令0.1,1.0 V的响应结果分别如图6、7所示,试验结果见表2。

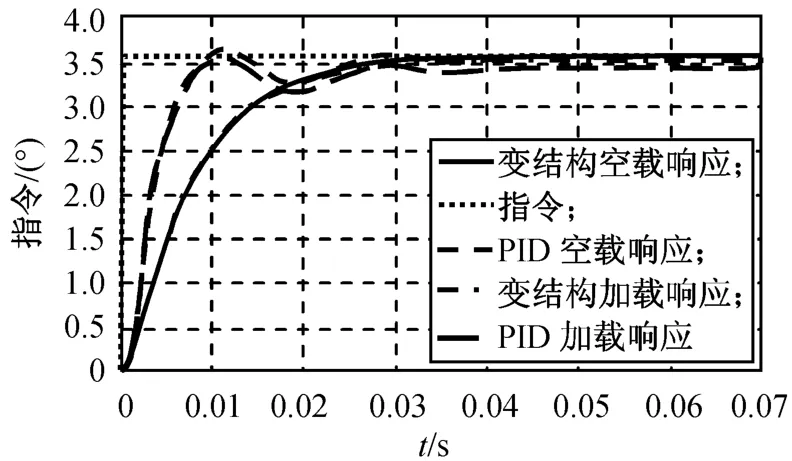
图6 有负载0.1 V阶跃响应Fig.6 0.1 V step response with load

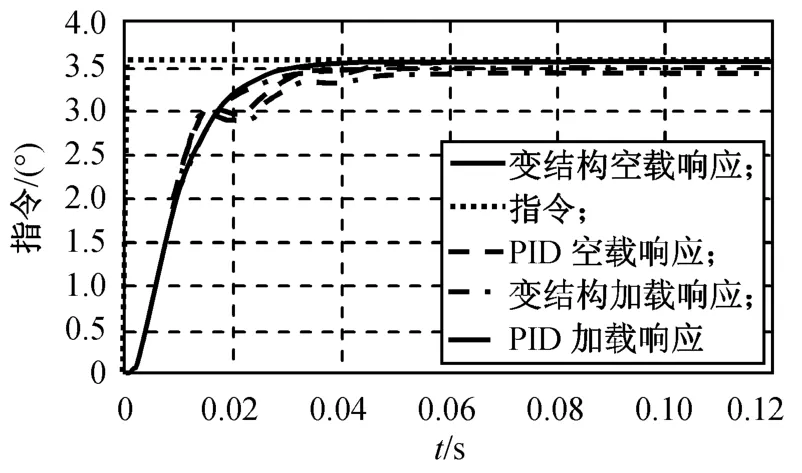
图7 有负载单位阶跃响应Fig.7 Unit step response with load

由图6、7可知：对PID控制算法,空载和加载时,舵偏指令3.6°的响应曲线变化很大,加载时存在静差,负载越大,静差越大,在阶跃指令下1 V达到0.5°,且为达到一定快速性,设计的PID阻尼较小,使小信号时有一定的超调;对VSS算法,不同负载下的静差很小,空载和加载时的响应曲线几乎重合。由此可见,所设计的VSS算法的抗负载能力优于传统PID。

表2 负载单位阶跃响应对比结果Tab.2 Results of unit step response with load

3.3 抗干扰

3.3.1 力矩干扰

为考察整个舵系统抗负载干扰能力,在电机输出中加入等效干扰力矩0.1 N◦m,所得系统响应如图8所示。

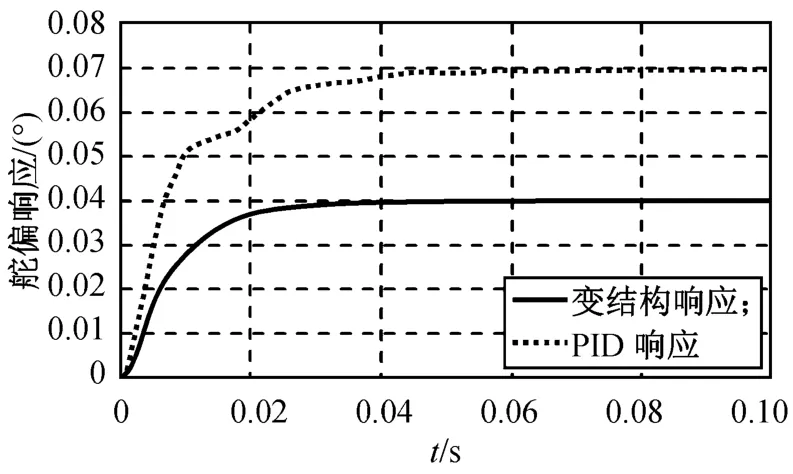
图8 电机干扰力矩0.1 N◦m时舵偏响应Fig.8 Helm deflection angle responsewith 0.1 N◦m disturbing torqueon motor

由图8可知：在干扰力矩0.1 N◦m作用下,PID算法需舵偏0.07°才能抵消干扰,且调节时间(95%)为33 ms,而变结构控制算法只需舵偏0.04°就能抵消干扰,调节时间仅为24.1 ms。可见对舵系统的干扰力矩,VSS的抗干扰性优于PID。

3.3.2 舵偏干扰

为考察整个舵系统抗舵偏干扰能力,在舵偏输出位置加入舵偏干扰2°,所得系统响应如图9所示。

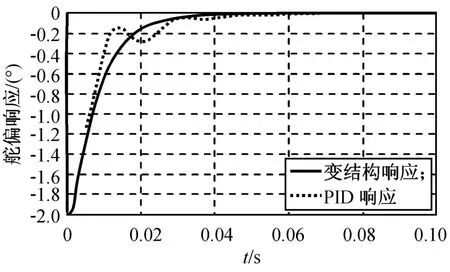
图9 舵偏干扰2°时系统响应Fig.9 System responsewith 2°disturbing helm deflection angle

由图9可知：在舵偏干扰2°作用下,PID算法需耗时25.4 ms才能调节到5%误差带内,而变结构为23.2 ms,耗时相对较PID短。

3.4 鲁棒性

3.4.1 转动惯量拉偏时响应

对直流电机,与电机模型密切相关的参数为力矩系数Kt、反电动势系数Ke、绕组电阻Ra、减速比Ki和等效转动惯量J等。对Kt,Ke,Ra,可根据相关电磁理论较准确地估得其数值,而Ki的误差一般较小,但由于结构的复杂性,J的精确值较难估算。因此,拉偏转动惯量以检验系统的抗参数摄动能力,结果分别如图10、11所示,试验结果见表3。

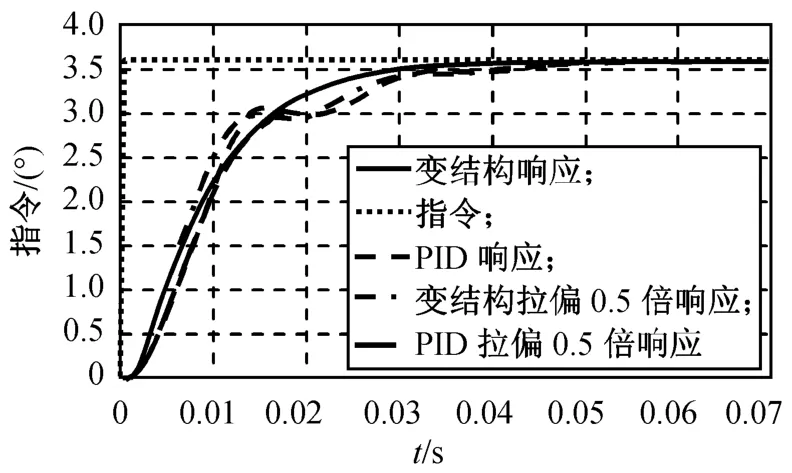
图10 转动惯量拉偏0.5倍单位阶跃响应Fig.10 Unit step response fore-and-aft rotational inertia changing half time

由表3可知：在转动惯量进行不同方向拉偏后,基于变结构控制的舵系统动态性能指标变化小于基于PID控制的舵系统,抗参数摄动能力较佳。

3.4.2 开环增益变化时响应

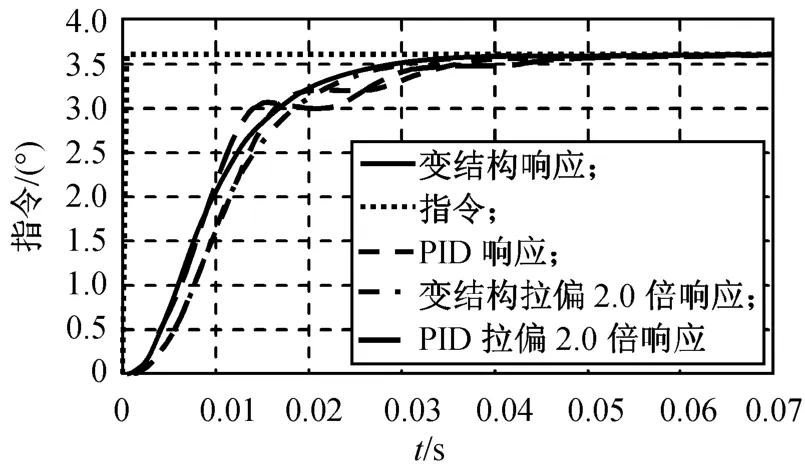
图11 转动惯量拉偏2倍单位阶跃响应Fig.11 Unit step responsef ore-and-aft rotational inertia changing twice times

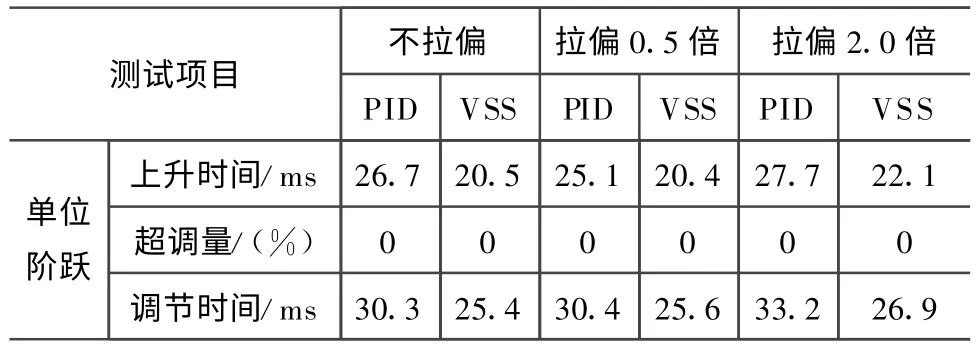
表3 转动惯量拉偏后单位阶跃响应比较结果Tab.3 Results of unit step response fore-and-aft rotational inertia changing

对式(3)的舵机传递函数方程,舵系统传递函数的等效开环增益与铰链力矩Mk和控制电压ua相关。实际飞行过程中,Mk,ua一直在变,故系统的等效增益也在不断变化。为检验设计的变结构算法对增益的适应能力,系统开环增益拉偏2.0,0.5倍的响应结果分别如图12、13所示,试验结果见表4。

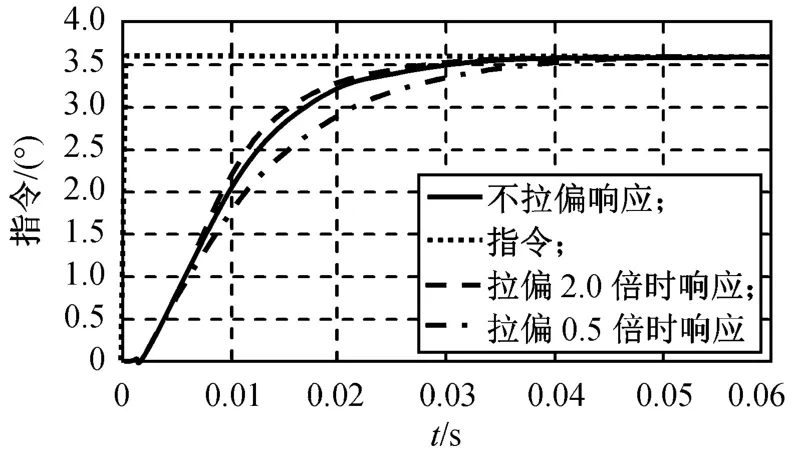
图12 开环增益拉偏0.5,2.0倍变结构算法单位阶跃响应Fig.12 Unit step responseof VSSwith open-loop gain changing half time and twice times

由仿真结果可知：PID控制算法在小信号指令下,系统增益发生变化时,系统响应也随之发生很大波动,特别是当增益减至为原来的1/2时,系统响应不仅变得很慢,而且静差很大;VSS控制算法对舵系统的增益变化不敏感,当增益增大为2倍或缩小为1/2时,系统的响应曲线变化很小,对增益变化的鲁棒性较优。

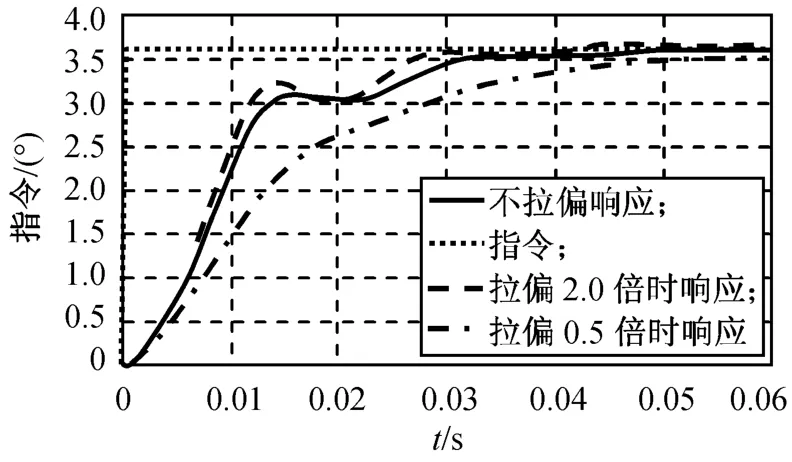
图13 开环增益拉偏0.5,2.0倍PID算法单位阶跃响应Fig.13 Unit step response of PID with open-loop gain changing half timeand twicetimes

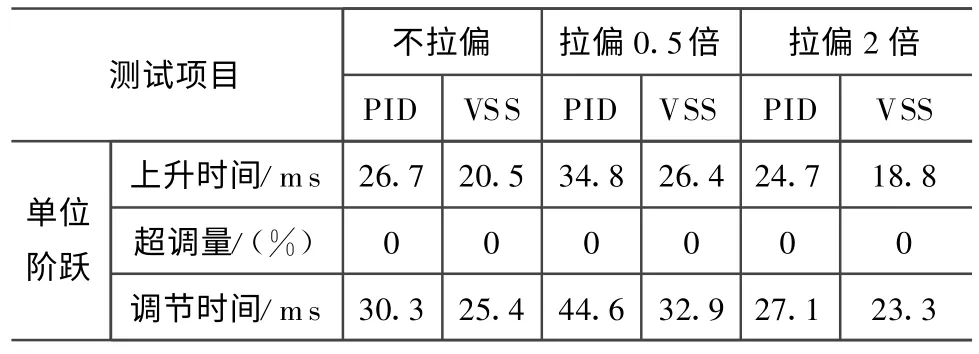
表4 开环增益拉偏后单位阶跃响应对比结果Tab.4 Results of unit step response fore-and-aft open-loop gain changing

4 结束语

本文对基于滑模变结构的电动舵机控制进行了研究。结合电动舵机的特点,根据推导的舵机状态方程,取舵指令偏差和偏差变化率为系统的状态变量,应用指数律以减小抖振,确定了系统的控制方程。仿真结果表明：与传统PID控制相比,基于VSS控制的电动舵机的快速性、抗负载能力、抗干扰能力和鲁棒性等均有一定的改善,且算法形式简单、状态变量少,工程性较好。

[1]周 军.变结构控制理论在导弹电动舵机系统设计中的应用[J].西北工业大学学报,1990,8(3)：273-280.

[2]王丰尧.滑模变结构控制[M].北京：机械工业出版社,1995.

[3]高国荣,王勋章.随动系统的变结构控制[J].电气自动化,1995(5)：7-11.

[4]刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社,2005.