包带连接力学分析与建模

白绍竣,梁 鲁,张 静,郑钢铁

(1.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001;2.清华大学 航天航空学院,北京 100084)

0 引言

包带连接分离机构广泛用于航天工程,其主要功能是实现卫星与火箭的连接和分离。包带机构由卡块、包带和爆炸螺栓等部件组成。在装配中,通过扭转两端的预紧力螺栓控制包带中的预紧力,由控制卡块对上下连接环的夹紧力实现连接。当飞行器到达目的地后,爆炸螺栓起爆解锁实现星箭分离。

包带连接对结构的刚度影响非常大,直接关系系统的动力学特性。随着有限元仿真技术的成熟,对卫星和火箭进行有限元建模分析已成为一种常用的工程方法,但对包带连接进行建模未见诸相关报道,即使关于包带连接其他方面的研究文献也非常少。如美国家航空航天局(NASA)的包带机构设计指导(文献[1])给出了包带机构设计时的注意要点;文献[2]对包带安装预紧力和连接刚度作了简单分析;文献[3]用轴对称有限元方法对包带连接的承载能力进行了研究;文献[4、5]研究了矩形和V形截面连接箍装置的预紧力与应力间的关系,对包带连接研究有重要的参考意义。

部分有限元计算中,多将包带结构简化为一组短梁,短梁的位置与卡块相对应,以模拟由包带导致的结构刚度变化。这样虽可简化计算,特别是避免了非线性问题,但短梁的结构参数较难选择。虽可用参数识别或试凑等方法从实验中获得对应的参数,但包带的参数随力的幅值大小而变,特别是在动载荷作用时参数不能简单认为是定常。因此,直接进行包带的建模是保证计算结果的可靠性和正确性的一条重要技术途径。

本文用有限元方法对包带连接的力学建模进行了研究。

1 包带有限元模型

一典型包带连接机构如图1所示。包带连接力学行为复杂,其中涉及多个部件的相互接触,与安装预紧力等因素关系密切。首先需对包带预紧力、连接环与卡块间的作用力,以及两连接环间的作用力进行分析,再根据接触力在连接环周向的分布将其等效到单元节点上。另外,建立卫星有限元模型时,对连接环常采用梁单元建模。因此,本文分析均在梁单元的基础上进行,且要求上下连接环的单元划分形式一致,上下节点相互对应。

图1 包带连接分离机构Fig.1 Marman clamp band system

1.1 预紧力分析与节点力等效

预紧力是包带连接安装时需考虑的最重要参数之一,对连接性能的影响非常大。预紧力可通过测量包带的应变获得,而包带的应变也是工程中确定预紧力的参照指标。

严格来说,包带与卡块间的压力fb、卡块与连接环间的正压力fN在卡块间隙以外的圆周上分布并不均匀。造成作用力不均的因素有摩擦力、卡块和包带的弯曲不均匀等多种。但一般包带的厚度较薄,卡块的间隙较小,并常采取降低接触面的粗糙度和在安装过程中加润滑剂等措施以减小摩擦力,这样可有效降低fb,fN的不均匀程度。因此,本文分析忽略了摩擦力并假设fb,fN在卡块间隙以外的圆周上均布,包带以及卡块受力如图2所示。根据力的平衡方程有

式中：Tb为包带内力;Rb为包带半径;α为卡块内斜面角度;m为卡块数量;ω为环向角度;ωi,′分别为第i个卡块的起始和截至的环向角度。对式(1)积分化简可得Tb,fb满足关系

图2 包带及卡块受力分析Fig.2 Loading analysis of strap and V-segment

当忽略摩擦力及卡块开口变形时,可认为fN的大小主要取决于包带的初始周长和变形后的周长,而包带周长又主要取决于连接环的变形和两连接环间的相对位移,因此在有限元模型中体现为包带周长取决于连接环节点的位移。为分析包带周长与连接环节点位移间的关系,需引入包带节点,每个包带节点对应一对相互对应的上下连接环节点,且假设它们间有确定的约束关系,根据约束关系可将包带节点的自由度转为对应的连接环节点自由度,故引入包带节点并不增加有限元模型的分析自由度。设带节点的初始位置为[xb0yb0zb0]T,它们与对应的上下连接环节点的初始位置分别为满足关系

为简化问题,考虑包带节点仅有3个位移自由度。设其与对应的上下连接环节点位移[u′ v′ w′]T,[u v w]T间的关系满足

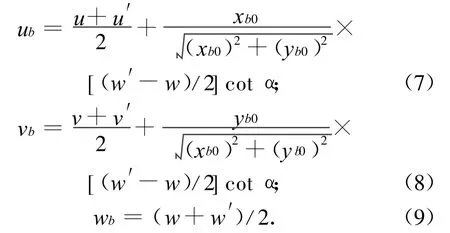
式(7)、(8)右端第二项表示了上下连接环单元节点轴向位移w′,w与对应包带节点位移ub,vb间的关系,如图3所示。图中：实线为连接环与卡块未发生位移时的状态;虚线为连接环发生一定轴向位移后的状态。将包带节点的初始位置与位移相加即可得发生位移后包带节点的位置[xbybzb]T。

图3 连接环轴向位移与卡块径向位移的关系Fig.3 Relationship between axial displacements of adapter rings and radial displacement of V-segment

在有限元模型中,可用所有相邻包带节点间距离的和近似代替包带的周长c(显然连接环划分单元数越多,周长就越精确),即

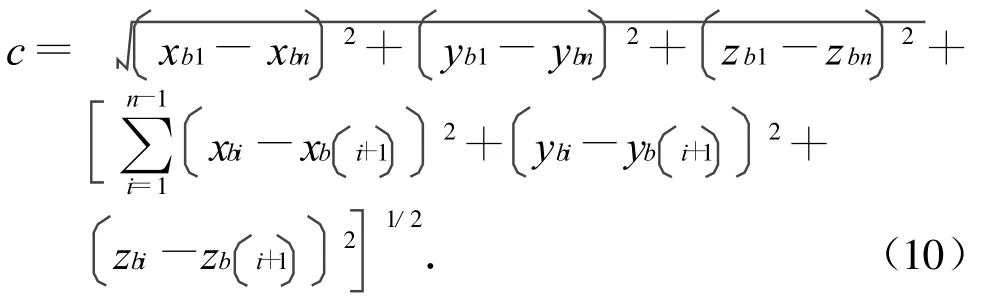
式中：xbi,ybi,zbi为各包带节点的位置;i=1,…,n。此处：n为连接环划分的有限单元数。由此可得

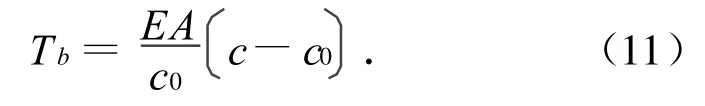
式中：c0为Tb=0时的包带周长;E为包带材料的弹性模量;A为包带的截面积。联立式(2)、(3)、(11),可得

fN对截面形心的转矩

式中：dN为截面形心至fN的垂直距离,如图4所示。

为分析fN在单元节点上的等效节点力,需先建立一局部坐标系,坐标系的Y向指向连接环的轴心线,Z向与连接环的轴心线平行,如图5所示。在沿连接环的圆周方向,由于卡块间的间隙,fN的实际作用长度为连接环周长的倍。此处：δ为卡块间隙的角度(如图2所示)。故在每个单元上亦假设fN的作用长度为单元长度的倍。则fN在上下连接环单元节点的等效载荷向量可表示为

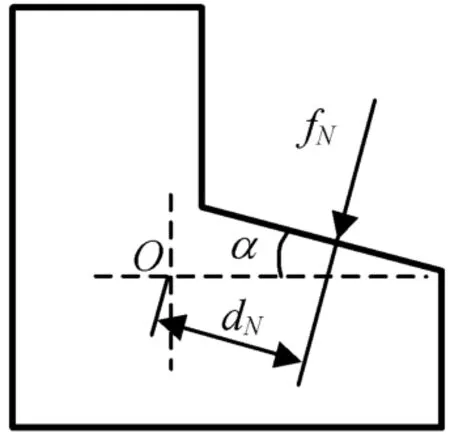
图4 连接环截面受力Fig.4 Loading of adapter ring section

式中：l为单元长度。此处：忽略了fN引起的Y、Z向的转矩。

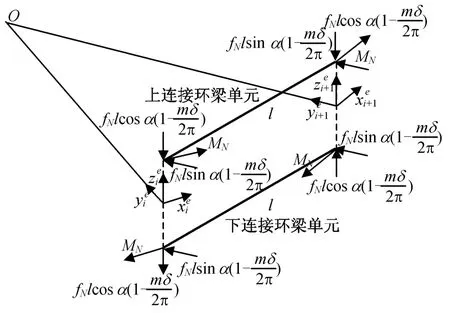
图5 包带环箍力在单元节点上的等效Fig.5 Equivalent node loads of clamp hoop force

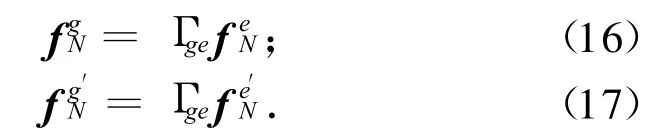
式中：Γge为单元坐标至整体坐标的转换阵。再跟据节点组装后可得整体坐标系中的等效单元节点载荷向量FN。

1.2 连接环接触力分析与节点力等效

上下连接环之间接触力的分析采用局部坐标系。

由于包带预紧力的作用,卡块将上下连接环紧紧地夹在一起,使初始状态的上下连接环间就有一定的相互作用力。可认为相互作用力的大小主要取决于上下连接环间的轴向相对位移Δw=w-w′及上下连接环截面转角θ,θ′,其变形几何关系如图6所示。图中：楔形区域为假设的接触变形区域;hc,lc为接触变形区域的相关尺寸,分别是接触变形区域的深度和长度,且

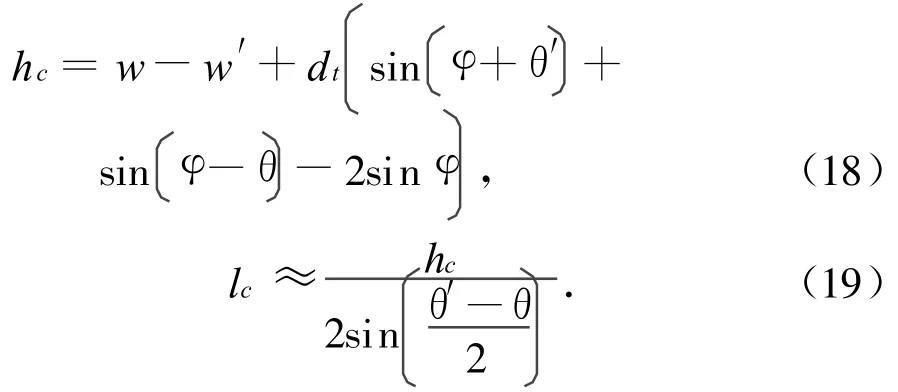
此处：dt,φ为与连接环截面形状和尺寸有关的参数。

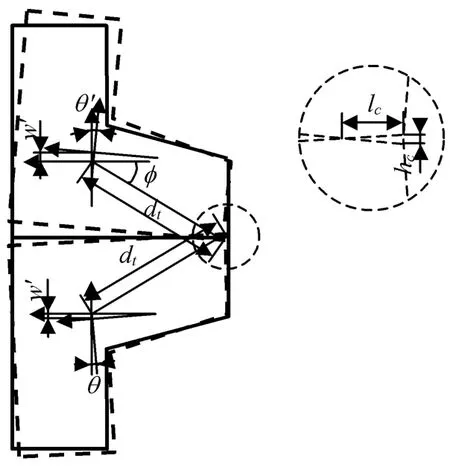
图6 连接环截面变形Fig.6 Deformation of section of adaptor rings

根据两连接环的接触状态,即接触变形区域的长度lc与连接环截面宽度dl的关系将接触力分为3个阶段：脱离接触阶段(阶段Ⅰ),lc=0;部分接触阶段(阶段Ⅱ),lc＜dl;完全接触阶段(阶段Ⅲ),lc≥dl。其中后两个阶段的接触力在截面内的分布假设如图7所示。分布力pc可表示为

图7 两连接环间的接触力分布Fig.7 Distribution of contact forceat stageⅡandⅢ

式中：ρ为表征两连接环接触刚度的常数,即由接触引起的局部变形刚度,与连接环的材料、形状尺寸和摩擦因数等有关,很难给出精确的数值,根据接触力学中的理论,一般可取为。此处：Er为连接环材料的弹性模量。

在沿连接环圆周方向上,假设接触力pc在以节点为中点的每个单元长度内均布,则其等效节点力和相对截面形心的等效节点力矩可用分段形式分别表示为

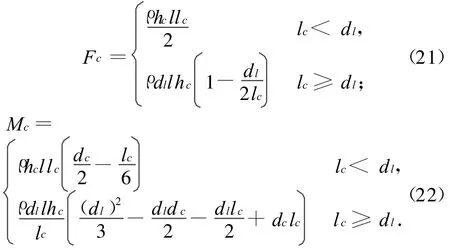
在局部坐标系中可表示为节点载荷向量形式

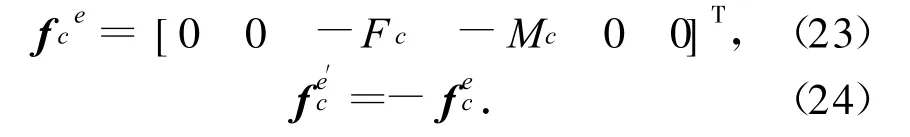
载荷的方向如图8所示。

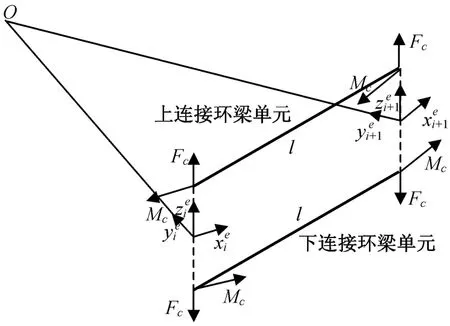
图8 连接环接触力在单元节点上的等效Fig.8 Equivalent nodeloads of contact force between twoadaptor rings

式中：Γge为从单元坐标系至整体坐标系的转换阵。根据节点进行组装,可得整体坐标系中的等效单元节点载荷向量Fc。

2 模型求解及其线性化

对含包带连接的航天器结构的有限元模型,其整体平衡方程可表示为

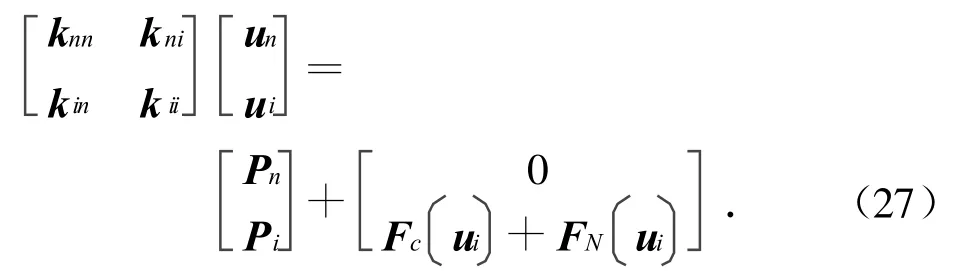
式中：k为刚度阵;u为位移;P为外载荷;下标n,i分别表示非包带连接界面自由度和包带连接界面自由度;ug为整体节点的位移,且ug=[unui]T;Fc,FN为包带连接接触力的等效节点载荷。

因式(27)中有非线性项Fc+FN,是一个非线性代数方程组,故本文用New ton-Raphson法求解。定义平衡方程的余量

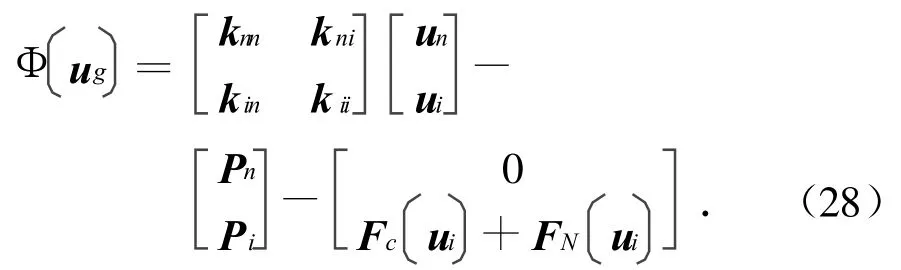
选定一初始估值,进行迭代

结构的固有频率和模态是工程中普遍关心的动力学参数,而对一个非线性系统,尚无成熟办法求解其固有频率和模态。对非线性系统常采用线性化处理,本文在静力平衡位置处进行泰勒展开并忽略高次项对方程进行线性化,即采用在平衡位置处求得的Kg近似替代系统的刚度阵进行动力学计算。线性化后系统的动力学方程可表示为

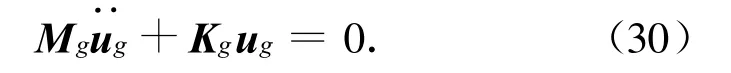
式中：Mg为整体结构的质量阵。对卡块与包带的质量,可用将卡块和包带的总质量均布到各连接界面节点上方法等效。

3 应用

为验证本文提出的方法,将其用于某卫星的有限元建模。该卫星有2个基本相同的包带连接(如图9所示)。其中：包带Ⅰ用于星箭分离,包带Ⅱ用于分离变轨发动机。由包带连接的各部分结构的有限元模型均为根据部件各自单独的试验结果修正后的模型。因此,可排除其他结构的建模误差而验证包带连接力学模型的准确性。计算中,采用的卫星有限元模型在通用商业有限元软件中建立,并输出系统的刚度矩阵和载荷向量(所输出的系统刚度矩阵中不含包带连接刚度阵kbb);再读出输出的系统刚度阵和载荷向量并编程,根据包带预紧力和初始估计位移值确定FN,Fc并按式(29)进行迭代,求得位移ug,在ug处进行线性化获得近似包带连接刚度kbb;将kbb导入有限元软件中计算模态。取包带连接相关参数为ρ=2×1010N/m2;φ=π/9 rad;l=59.32 mm;α=π/12 rad;dl=12 mm;E=2×1011Pa;A=40 mm2;dc=6 mm;dt=6.25 mm;Rb=453.5 mm;dN=5 mm;Tb=2×104N;δ=π/90 rad;m=26个。计算所得前三阶弯曲振型如图10～12所示。为分析包带连接对结构固有频率的影响,分别将计算结果与刚性连接和试验结果进行了比较,结果见表1。由表可知：采用包带连接模型后的计算结果更接近于试验值,且包带连使结构的固有频率明显降低,其影响需在建模和设计时给予充分考虑。

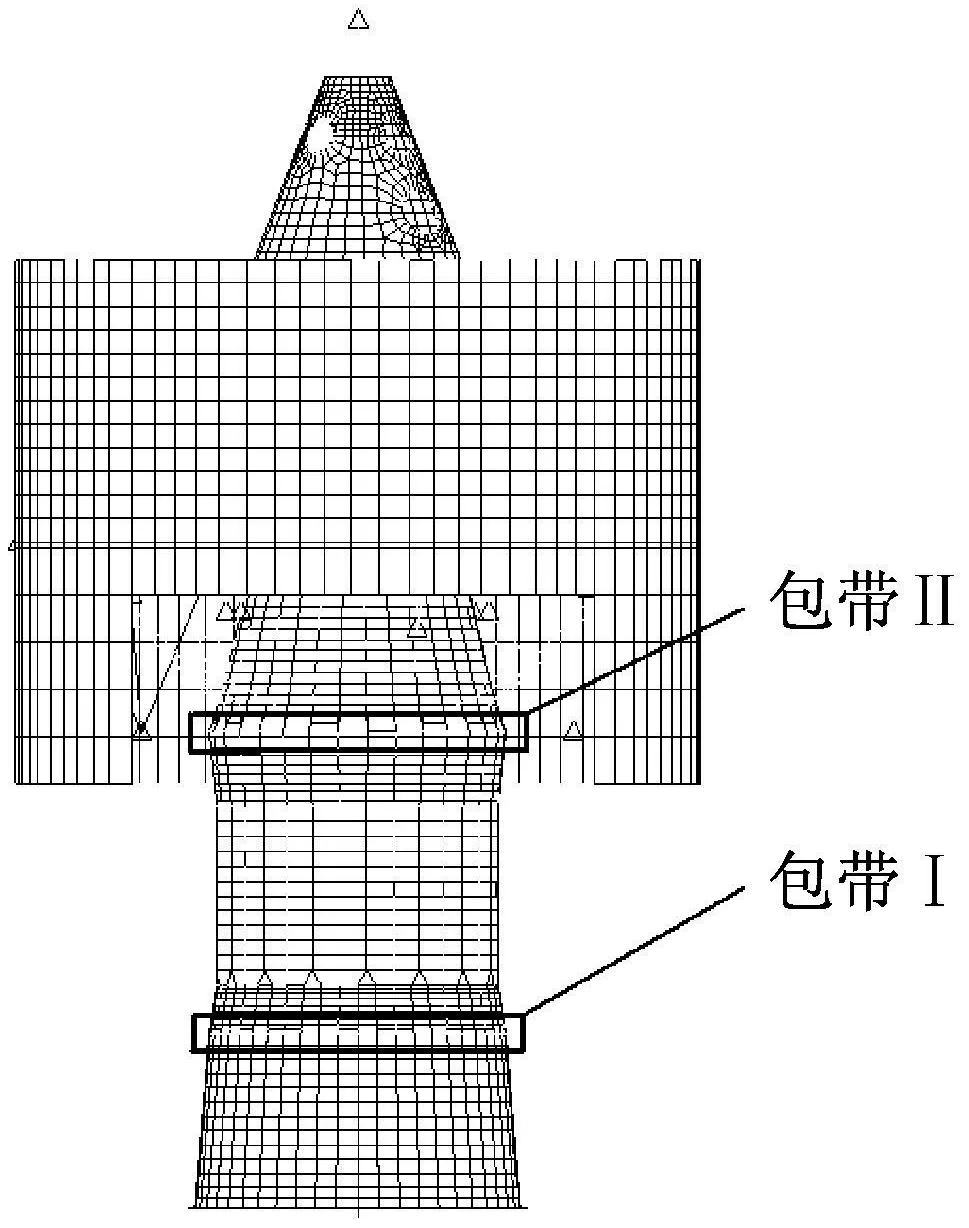
图9 卫星有限元模型Fig.9 Finite element model of some satellite

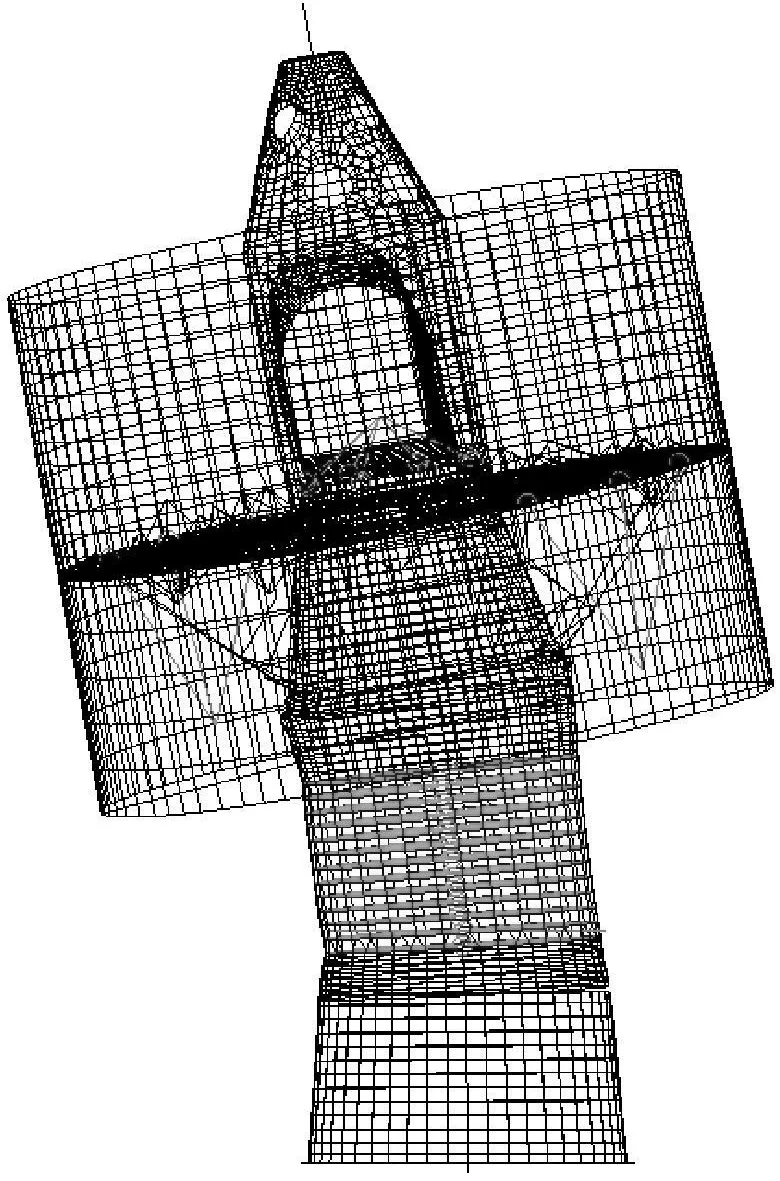
图10 卫星的一阶弯曲模态(12.63 Hz)Fig.10 Modal shape of some satellitewith 1 order of bend(12.63 Hz)

图11 卫星的二阶弯曲模态(41.08 Hz)Fig.11 Modal shape of some satellite with 2 order of bend(41.08 Hz)

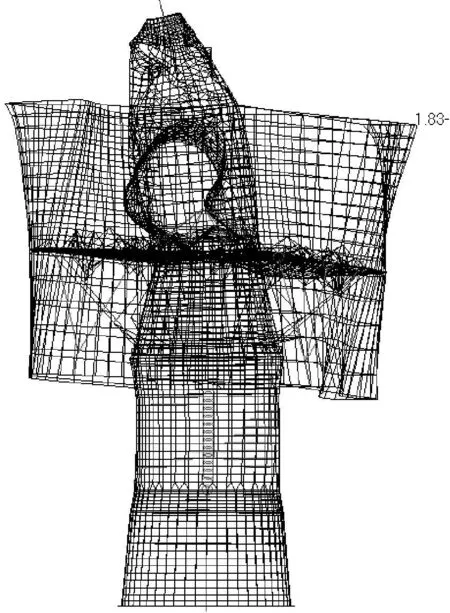
图12 卫星的三阶弯曲模态(66.41 Hz)Fig.12 Modal shape of some satellitewith 3 order of bend(66.41 Hz)

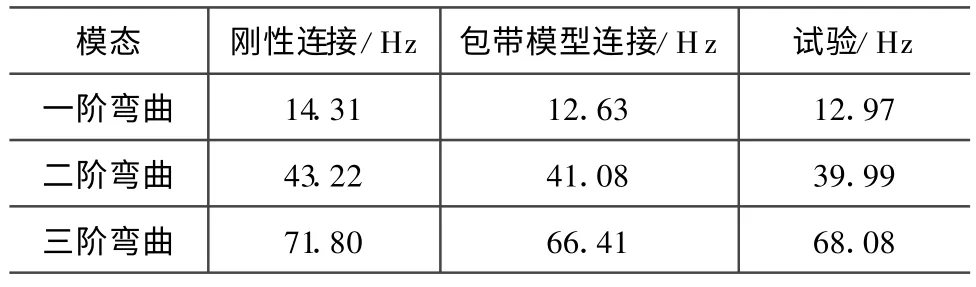
表1 计算结果与试验比较Tab.2 Comparison of simulation and experiment

4 结束语

本文对包带连接分离机构进行力学建模,分析了包带预紧力、卡块与连接环间的接触力,以及两连接环间的接触力,并在此基础上将接触力等效为单元节点力实现了包带连接的有限元建模,用泰勒展开对模型进行线性化,讨论了包带连接对结构固有频率的影响。某卫星的算例结果验证了方法的有效性。但包带连接涉及的接触面多,接触面的摩擦和常伴有的应力集中与塑性变形均增加了包带连接力学行为的复杂度。另外,动态接触过程中会发生接触面间的滑动及接触分离等现象,在进入接触过程中还常伴有冲击发生,这些尚需作进一步研究。

[1]NASA Goddard Space Flight Centre.Marman clamp system design guidelines[R].GD-Ed-2214,2000.

[2]唐乾刚,孙世贤.包带式星箭紧锁预紧力分析[J].国防科技大学学报,1996,18(2)：20-25.

[3]TOLLA R D,ERNST M.Nonlinear finite element evaluation of marman clamp structure capability[R].AIAA 1994-1346.

[4]SHOGHI K,RAO H V,BARRANS SM.Stress in a flat section band clamp[J].Int Journal Mechanic Science,2003,217(7)：821-830.

[5]SHOGHI K,BARRANS S M,RAO H V.Stress in V-section band clamps[J].Int.Journal Mechanic Science,2004,218(3)：251-261.