液氢加注系统竖直管道内Taylor气泡的行为特性

马昕晖 徐腊萍 陈景鹏 宋建军

(装备学院 北京 101416)

液氢加注系统竖直管道内Taylor气泡的行为特性

马昕晖 徐腊萍 陈景鹏 宋建军

(装备学院 北京 101416)

针对液氢加注系统竖直管道内气液两相流实验化困难的问题，运用建模仿真的方法建立了竖直管道内Taylor气泡的运动模型，对Taylor气泡的形成过程、大小以及充分发展的Taylor气泡上升速度进行了研究。采用VOF方法对气液两相的交界面进行追踪，并引入CSF模型对两相间的表面张力进行计算。仿真结果表明:Taylor气泡是由弥散的小气泡聚合而成，根据泡状流向弹状流转变得出的Taylor气泡的临界长度比处于发展中的Taylor气泡长度要小，充分发展的Taylor气泡基本上以0.226 5 m/s的速度匀速上升。

液氢加注系统 竖直管道 间歇泉现象 Taylor气泡 VOF方法

1 引言

液氢加注系统中间歇泉现象主要是在液路系统的竖直管道里发生，由于管道漏热使管内产生弥散的小气泡，从而形成两相流。气泡形成后会向阻力较小的管道中心移动、积聚并不断增多，聚集到一定程度后开始互相干扰、聚合，最终会形成一个弹状头冠的弹状流气泡，称之为Taylor气泡(又称弹状气泡)，如图1所示。该气泡继续上升，将其前方的液体挤出管道，最终形成喷发而产生间歇泉现象［1］。因此，Taylor气泡的研究对于避免液氢加注系统竖直管道内间歇泉现象的产生具有重要的实际意义。

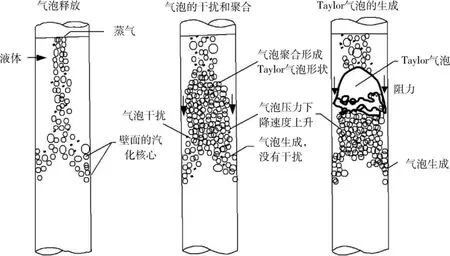
图1 Taylor气泡形成过程示意图Fig.1 Formation schematic diagram of Taylor bubble

目前国内外对于Taylor气泡的研究比较多，但大部分都是在常温状态下对Taylor气泡的研究，低温状态比较少。低温状态下对Taylor气泡的研究主要是以液氮为工质，对液氢中的Taylor气泡研究很少。王淑华等［2］对两个连续Taylor气泡在垂直管中上升进行了数值模拟，得到两个连续Taylor气泡上升过程中尾随气泡的运动特性;张亮［3］搭建了可视化实验台，对低温液氮垂直输送管道中的气泡聚合、上升过程进行了研究，拟合了Taylor气泡速度分布公式，并对气泡长度进行了研究;Taylor和Dumitrescu对弹状流中气泡的上升速度进行了大量的实验和理论研究，建立了Rayleigh-Taylor气泡模型［4-5］。本文将对液氢加注系统竖直管道内Taylor气泡的行为特性进行研究。

气泡运动是一种典型的具有气液界面变形的非定常流动，准确确定运动界面、处理好界面物性变化是求解关键［6］。本文采用Euler法中容积跟踪技术的VOF方法跟踪界面，在气泡运动仿真模拟中，引入CSF模型来处理表面张力，采用Fluent软件对低温液氢竖直管道内静置液氢中的Taylor气泡进行仿真模拟。

2 建模仿真基础与方法

2.1 控制方程

竖直管道内流体运动要遵循3个最基本的守恒定律:质量守恒定律、动量守恒定律以及能量守恒定律，在流体力学中具体表现为连续性方程、动量方程和能量方程［7］。对于这3个方程，可以写成统一的表达式:

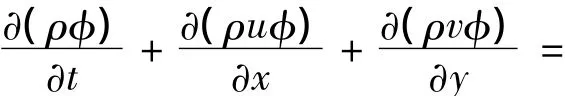
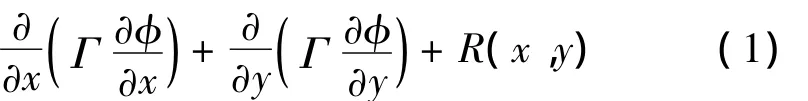
式中:ρ为密度，φ为一个变量，Γ为广义扩散系数，R(x，y)为广义源项。采用同位网格下的贴体坐标并用有限体积法(FVM)离散上面的方程，扩散项采用中心差分的格式，对流项采用一阶迎风的格式，压力与速度耦合的问题采用PISO算法。

2.2 边界条件

温度为20.93 K时，液氢与氢气的密度分别为70.96 kg/m3、1.331 kg/m3，粘度分别为 1.32 ×10-5Pa·s、1.1 ×10-6Pa·s。

液氢加注系统液路系统管道直径d为80 mm，选取其中一段2 000 mm的二维竖直管道为计算域，来研究竖直管道内静置液氢中的Taylor气泡。对这一段管道进行均匀网格划分，相间差值使用几何重构的方法。采用控制容积法对偏微分方程进行离散，压力和速度的耦合采用PISO方法，时间步长为0.001 s。

2.3 VOF方法

运动界面跟踪问题的解决方法有maker particle法、height function法、线段法、VOF方法以及Level set法等［8］，本文采用 VOF方法。VOF方法是 Hirt和Nicholas在1981年首先提出的［9］，通过一个体积函数F，使F的值等于1个单元内流体体积与该单元体积之比，若F=0，单元内不含流体，若F=1，单元内充满流体，若0＜F＜1，单元内含有自由界面。在二维中，F守恒型传输方程如式(2):

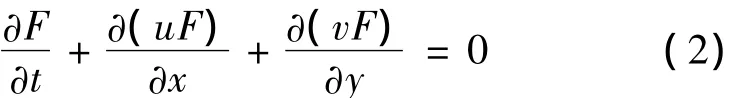
式中:u和v分别为主场沿x方向和y方向的速度。

研究多相流时，在每个控制体积单元里，所有相的体积分数之和等于1［2］。假设第q相的体积分数为αq，则在某控制体积单元内，若αq=0，单元内不含第q相;若αq=1，单元内充满第 q相，若0＜αq＜1，单元内含有其它相的自由界面，且αq满足方程:

式中n表示总相数。

每个控制体内混合流体的密度可以表示为:ρ=∑αqρq，粘性可以表示为:μ = ∑αqμq。各相之间界面的跟踪可通过求解体积分数的连续方程完成:

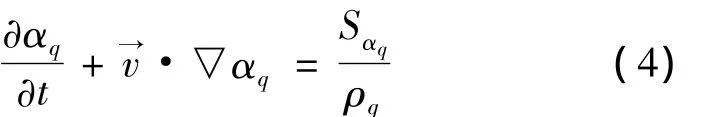
对于基本相，其体积分数不是由式(4)求得，而是由式(3)求得。

VOF方法在计算多相流时，只求解单一的动量方程，得到的速度场为各相共享，而各相的体积分数对动量方程的影响都是通过属性ρ和μ反映到动量方程中，如式(5)所示:

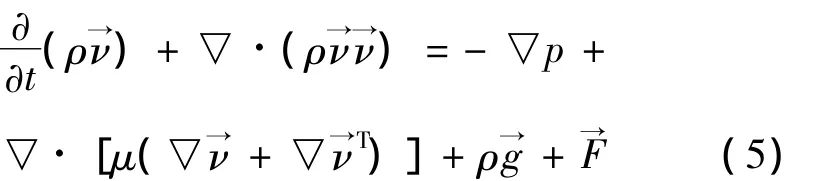
2.4 表面张力的求解

流体分子之间的相互作用使得流体表面形成了一层像皮肤一样的弹性边界，具有表面张力。表面张力的大小与流体物性相关，对运动界面的影响较大。本文采用由Brackbill等提出的连续表面张力模型(CSF)处理表面张力［10］。在该模型中，假定流场中两种工质边界区域具有有限厚度，这使得F在有限厚度界面区域形成一个过渡区域，从而使得F在整个过渡区域中成为连续函数。在此区域内，每一点上的表面力与该点的F的曲率成正比。当界面区域的厚度变化趋近于零时，就可以通过F点的曲率得到表面张力。在方程(1)中，源项可写成:

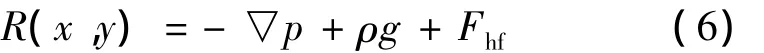
其中Fhf为表面张力。由CSF模型，界面上的表面张力为:

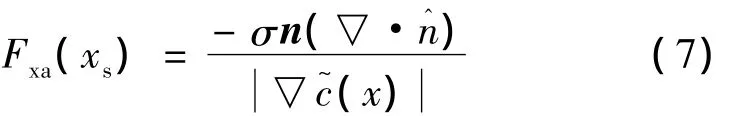
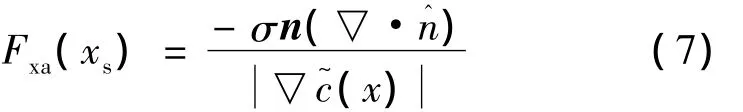
式中:σ为表面张力系数。因此可得:

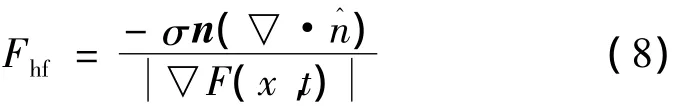
式中:

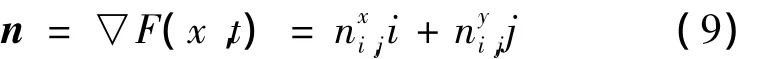
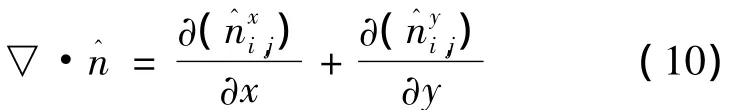
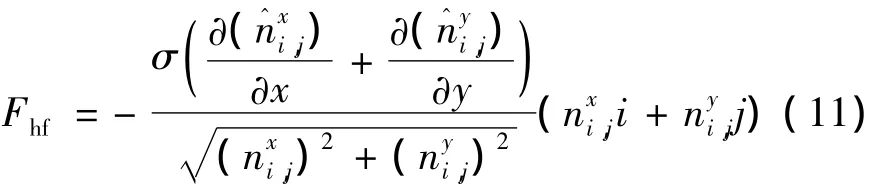
液氢表面张力系数σ(N/m)可以通过Macleod-Sugden 法［11］求得:

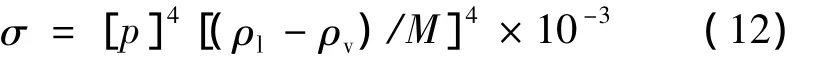
式中:［p］为等张比容，ρl、ρv分别为液体与气体的密度，g/cm3;M为摩尔质量，g/mol。

在1.013×105Pa大气压下，温度为20.93 K时，液氢:ρl=0.070 96 g/cm3;气氢:ρv=0.001 331 g/cm3;氢原子的［p］值为15.5;氢的摩尔质量 M=2.015 94 g/mol;求得σ=0.001 314 3 N/m。

3 模型仿真结果分析

3.1 Taylor气泡形成的过程

液氢加注系统液路系统竖直管道内Taylor气泡是由弥散的小气泡聚合而成的。由于管道漏热，会使管道内的液氢受热汽化成小气泡，这些气泡存在一个临界直径［12］:

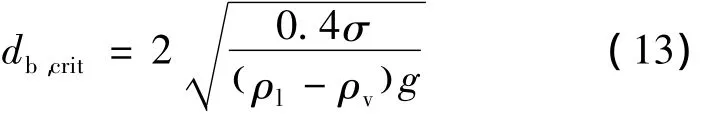
当气泡直径小于这一临界直径时，气泡为球形并沿光滑曲线(直线)运动，当气泡直径大于这一临界直径时，气泡开始变形，并在运动的过程中表现出不规则的布朗运动，气泡之间发生碰撞、聚合和破裂。管道内弥散气泡如图2所示，大部分气泡直径大于临界直径，因此，弥散的小气泡在管道内运动过程为不规则的布朗运动。

一个气泡在邻近气泡的激活下，速度将增大，并且会超过该气泡上部的气泡或与气泡聚合成一个更大的气泡，由于管道中心阻力较小，气泡会向管道中心移动并积聚，经过一段时间后，管道内气泡聚合成Taylor气泡，如图3所示。

管道纵向中心截面速度分布如图4所示，由于下部气泡上升的速度比上部气泡快，管道内Taylor气泡下方的速度分布由下至上呈减小的趋势;图中Taylor气泡上升过程中尾端存在涡流，使靠近Taylor气泡尾端部分的两相流上升速度大幅度增加;而Taylor气泡上升的过程中，管道内形成对流，管道壁面附近液体向下流动，底部管道中心的速度变化比较大。

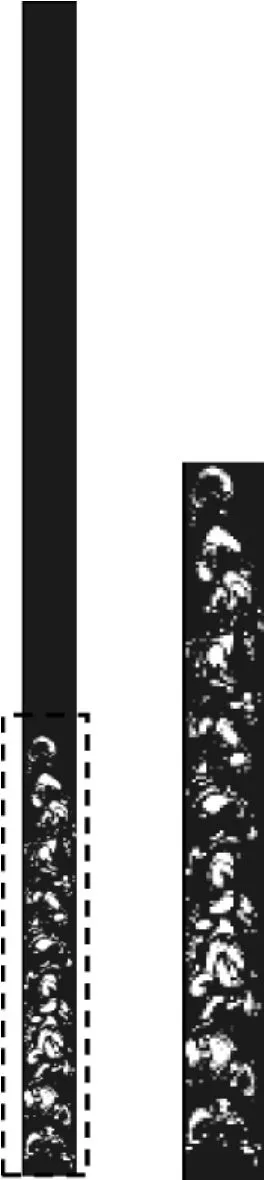
图2 弥散气泡Fig.2 Dispersion of small bubbles

图3 Taylor气泡Fig.3 Taylor bubble

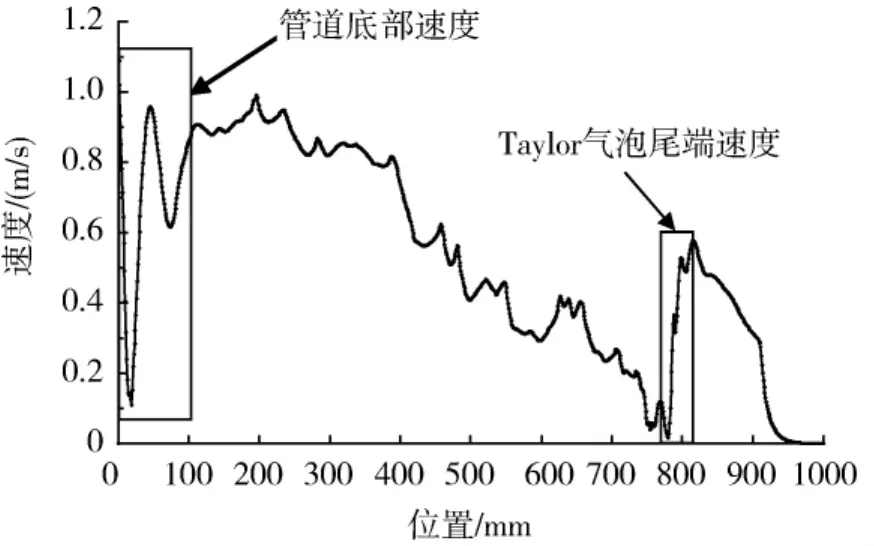
图4 管道纵向中心截面速度分布曲线图Fig.4 Velocity distribution curve of tube’s vertical center cross-section

3.2 Taylor气泡的长度

弥散的小气泡在管道内聚合后，形成Taylor气泡，这时两相流由泡状流动向弹状流动转变，气泡的临界长度为 Ls(m)，则有［3］:

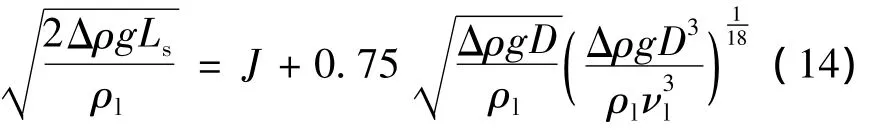
式中:D为管道内径，m;J为表观速度，m/s，静置液氢中为0 m/s;ρl为液氢密度，ρv为氢气密度，Δρ=ρl-ρv;νl为液氢动量粘性系数，Pa·s。经过仿真得到竖直管道内Taylor气泡的长度如图5所示。

图5 Taylor气泡长度示意图Fig.5 Schematic diagram of Taylor bubble’s length

由式(14)得出的 Taylor气泡临界长度 Ls为0.051 6 m，比处于发展中的Taylor气泡长度L要小。这是因为Taylor气泡形成后，气泡间由于存在相互的影响，Taylor气泡与其它小气泡继续聚合，形成更大的气泡，气泡长度将比Taylor气泡刚刚形成时要大。从而发展中的Taylor气泡长度L要大于Taylor气泡刚刚形成时的临界长度Ls。

3.3 Taylor气泡上升的速度

在静置的竖直管道内，对称且边界层压力分布连续的充分发展的Taylor气泡上升速度为［4-5］:

式中:g为重力加速度，m/s2;D为管道内径，m;K为与流体性质有关的系数，在水-空气两相流中K取为0.35，在液氢-氢气两相流中K值可通过仿真实验结果求得。

本文中Taylor气泡的上升速度可以通过式(16)确定:

式中:x1、x2为 t1、t2时刻 Taylor气泡顶部的位置;Δt=(t2-t1)为时间差。得到Taylor气泡的上升速度曲线图如图6所示。

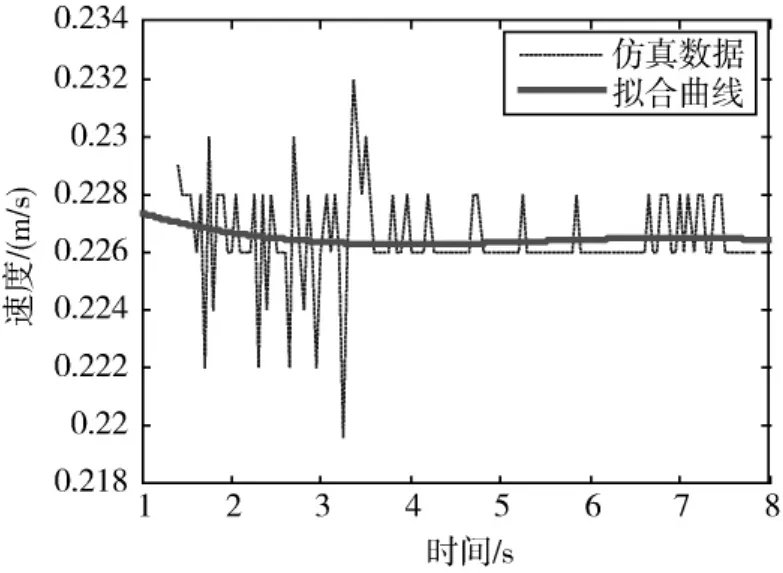
图6 Taylor气泡速度曲线图Fig.6 Curve of Taylor bubble’s velocity

由图6可知，低温液氢加注液路系统竖直管道内充分发展的Taylor气泡速度基本在0.226—0.228 m/s这个区间内波动，由于存在读数等误差，基本上可以认为气泡匀速上升，上升速度为0.226 5 m/s。而由式(15)求得常温下内径相同的管道内水-空气两相流中Taylor气泡上升速度为0.310 1 m/s，比本实验中Taylor气泡上升速度要大，这是因为低温液体在低温下与常温下水的热力学物性有明显不同，从而K的取值不同，求得的Taylor气泡上升速度不同。

张亮［3］在以低温液氮为工质进行的可视化实验中，对气泡聚合过程进行了分析，拟合了低温液氮在竖直输送管道中弹状流气泡的速度分布公式，由实验结果拟合出的K值为0.284。本实验中测得低温液氢中Taylor气泡的速度为0.226 5 m/s，由式(15)可求得在本实验中K的值为0.256，与张亮实验中求得的K值接近。

4 结论

对低温液氢加注系统竖直管道内静置液氢中Taylor气泡进行了仿真模拟，研究了Taylor气泡的形成过程、气泡大小与上升速度，得到以下结论:

(1)液氢加注系统液路系统竖直管道内的Taylor气泡是由管道漏热后产生的弥散小气泡聚合而成，管道内两相流的速度由下至上呈减小的趋势;

(2)Taylor气泡形成的临界长度与管道内径、气液物性有关，由于Taylor气泡上升过程中不断与其他小气泡聚合，Taylor气泡的临界长度要小于发展中的Taylor气泡的长度;

(3)低温液氢的热力学物性在低温下与常温下水的热力学物性有明显的不同，因此在Taylor气泡充分发展后，其上升速度为0.226 5，比常温下内径相同的管道内水-空气两相流中Taylor气泡上升速度小。这是因为K值不同，本实验中K的值为0.256。

通过对液氢加注系统液路系统竖直管道内Taylor气泡的仿真模拟，掌握了竖直管道内Taylor气泡大小以及上升的速度，为进一步研究竖直管道内间歇泉现象奠定了基础。

1 张 亮，林文胜，鲁雪生，等.低温液体输送系统间歇泉现象机理分析与消除措施［J］.低温与超导，2002，30:1-6.

2 王淑华，刘夷平，张 华，等.两个连续Taylor气泡在垂直管中上升的数值模拟［C］.第二十届全国水动力学研讨会文集，2002:259-264.

3 张 亮.垂直输送管路中低温流体的间歇泉现象研究及自然循环分析［D］.上海:上海交通大学，2004.

4 Takemoto Takatoshi，Matsuzaki Mitsuo，Aritomi Masanori，et al.The coalescence mechanism of multiple slug bubbles［J］.Journal of Nuclear Science and Technology，1999，36(8):671-682.

5 R Moissis，P Griffith.Entrance effect in two phase slug flow［J］.Journal of Heat Transfer，TRANS ASME，Series C，1962，84:29-39.

6 李维仲，赵大勇，陈贵军，等.竖直流道宽度对气泡运动行为影响的数值模拟［J］.计算力学学报，2006，23(2):196-201.

7 王瑞金，张 凯，王 刚.Fluent技术基础与应用实例［M］.北京:清华大学出版社，2007.

8 陈大宏，李 炜.自由表面流动数值模拟方法的探讨［J］.水动力学研究与进展，2001，16(2):216-224.

9 Hirt C W，Nichols B D.Volume of fluid method for the dynamics of free boundary［J］.Journal of Computational Physics，1981，93:201-225.

10 Brackbill J U，Kothe D B，Zemach C.A continuum method for modeling surface tension［J］.Journal of Computational Physics，1992，100:335-354.

11 王福安.化工数据导引［M］.北京:化学工业出版社，1995.

12 Barnea D.Transition from annular flow and from dispersed bubble flow-united models for the whole range of pipe inclinations［J］.International Journal of Multiphase Flow，1986，12(5):733-744.

Research on Taylor bubble’s behavior in vertical tube of liquid hydrogen loading system

Ma Xinhui Xu Laping Chen Jingpeng Song Jianjun

(Academy of Equipment，Beijing 101416，China)

Because of the experimental difficulty of two-phase flow in a vertical tube for liquid hydrogen loading systems，a Taylor bubble movement model in vertical tube were established using modeling and simulation methods.The formation process，size and rising velocity of Taylor bubble fully developed were studied.VOF method was used to track the interface of two-phase flow and CSF model was introduced to calculate the surface tension between two phases.Simulation results show that Taylor bubble is polymerized from the small dispersed bubbles，the critical length of the Taylor bubble when the bubbly flow changing to slug flow is smaller than the Taylor bubble in the development，Taylor bubble fully developed is basically increasing in the uniform rate of 0.226 5 m/s.

liquid hydrogen loading system;vertical tube;geysering phenomenon;Taylor bubble;VOF method

TB611

A

1000-6516(2011)06-0066-05

2011-10-12;

2011-11-28

马昕晖，女，42岁，硕士、副教授。