氦原子间的范德瓦尔斯力与其半经验势函数的拼接构造

陈 煜 陈 硕

(1上海工程技术大学机械工程学院热能与动力工程系 上海 201620)

(2同济大学航空航天与力学学院 上海 200092)

氦原子间的范德瓦尔斯力与其半经验势函数的拼接构造

陈 煜1陈 硕2

(1上海工程技术大学机械工程学院热能与动力工程系 上海 201620)

(2同济大学航空航天与力学学院 上海 200092)

为了确定氦原子势函数的具体形式，通过分析氦原子间的范德瓦尔斯作用力，指出氦原子势函数可由其范德瓦尔斯排斥势和吸引势拼接构造而成，并得出了氦原子通用势函数的具体形式。结果表明:对于氦原子势函数，排斥力不再适宜采用原子中心间距r的-12次方的形式，而更适合采用指数形式的排斥项，因此其势函数通用形式中包括指数型排斥项以及分别由偶极相互作用、偶极-四极相互作用、四极-四极相互作用引起的吸引势，其中偶极相互作用为范德瓦尔斯吸引势的主要组成部分。

氦 范德瓦尔斯力 势函数 拼接构造

1 引言

范德瓦尔斯力(Van der Waals force)，又称为范德华力，通常认为，原子之间的范德瓦尔斯力共包括3种类型的力，即 Keesom力、Debye力以及 London力。分子间相互作用力与分子内力相比非常微弱。对于中性原子而言，在微弱的分子间作用力的组成中，Keesom力与Debye力很小，与实际上观察到的存在于中性原子之间的吸引力相差较大，因此London色散力被认为是唯一存在于惰性气体原子间的吸引力，是Van Der Waals吸引力组成中的重要部分之一，如果没有它的存在，惰性气体原子间的吸引力也将随之消失，因此，也就不会出现其对应的液体状态［1］。对于非极性和非激发态原子而言，在研究确定其原子间的相互作用时，通常会考虑到两种类型的力，一是由于电子交换而产生的排斥力，二是极化吸引力［2］。实际上，氦原子之间的吸引力非常微弱，以至于其沸点极低，很难被液化。根据氦原子的Van der Waals力，可将氦原子间的势函数写成方程(1)的形式［3］:

式中:urepulsive为Van der Waals排斥项，而uattrative为Van der Waals吸引项。

2 Van der Waals吸引力

2.1 偶极-偶极作用(dipole-dipole interaction)

Slater与Kirkwood最早采用微扰波函数计算得到了氦原子的极化率数值［4］，通过微扰波函数理论和相应的氦原子的极化率，得到了主要由偶极相互作用引起的氦原子之间的相互作用势函数的吸引项，如方程(2)所示，这种早期形式的势函数是就是由短程排斥势和长程范围内的表现为吸引力的偶极-偶极相互作用拼接而成，由此得到的势阱深度约为-8.9 K。

式中:u(r)为其势能吸引项，是原子中心间距r(单位:埃米，Å)的函数，采用的单位为尔格(erg，1erg=1×10-7J)。

2.2 四极作用

氦原子之间存在的Van der Waals力产生于二次极化，即中性原子的极化是由于另一个中性原子产生的。通常情况下，发生这种情况是因为第二个原子具有永久偶极距(permanent electric moment)。对于没有永磁极的原子而言，其间的范德瓦尔斯力产生于与量子跃迁有关的多极相互作用［2］。当原子之间的距离较远时，偶极相互作用在多极相互作用中占有绝大部分，以致于偶极-四极相互作用和四极-四极相互作用在通常情况下是被忽略而不予考虑的。Margenau同时指出，在多极相互作用中，四极-四极相互作用极小，但是偶极-四极相互作用需要予以足够的重视。在充分考虑了偶极-四极相互作用和四极-四极相互作用的情况下，在Slater与Kirkwood的研究基础上，Margenau利用类似的方法构造了氦的势函数，势函数的势阱达到了(-13.5±1.5)K。由此给出了氦原子势函数的吸引项如方程(3)所示，其中各组成项的大小及其对总的Van Der Waals势函数吸引项的影响如图1所示。

式中:u(r)为其势能吸引项，是原子中心间距r(单位:Å)的函数，单位:erg。

图1 Margenau提出的氦原子Van der Waals势函数吸引项Fig.1 Van der Waals attractive part of heliumpotential obtained by Margenau

Page认为虽然Margenau较全面地分析计算了偶极-四极、四极-四极相互作用对于氦原子间Van der Waals力的影响，但是在其研究系统中采用的近似二阶扰动方法缺少一定的精度，其认为Van der Waals势是微扰势在量子力学意义上的平均，因此采用变分计算方法处理势能函数的级数展开式的前两项［1］，得到了Van Der Waals势能吸引项计算方程(4)(单位:erg)，其中偶极-偶极相互作用、偶极-四极相互作用及其对总的Van Der Waals势能吸引项的影响如图2a所示。

同样借助于变分计算方法，将其应用于微扰势函数，利用更加复杂的变分函数以提高扰动势能的计算精度，得到了3项Van der Waals势能吸引项计算方程(5)(单位:erg)，其中偶极-偶极相互作用、偶极-四极相互作用、四极-四极相互作用及其对总的Van Der Waals势能吸引项的影响如图2b所示。

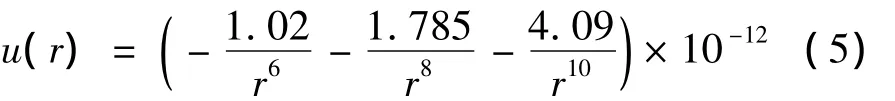
图2 Page提出的氦原子Van der Waals势函数吸引项Fig.2 Van der Waals attractive part of helium potential obtained by Page

根据不同理论计算得到的Van Der Waals势函数吸引项如图3所示。

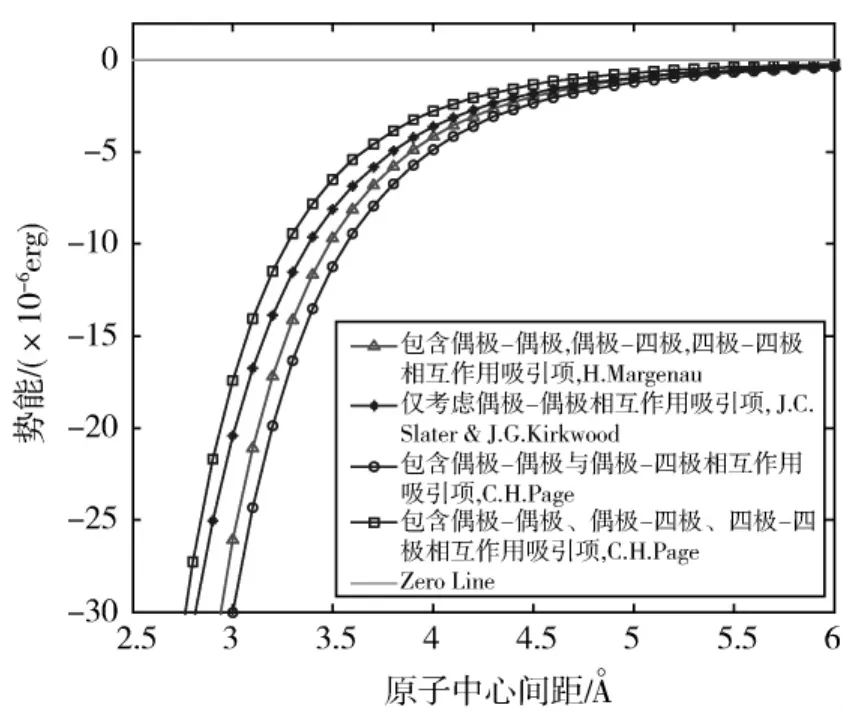
图3 偶极-偶极相互作用吸引项与附加偶极-四极、四极-四极相互作用吸引项Fig.3 Dipole-dipole interaction and including effect of dipole-quadrupole and quadrupole-quadrupole interaction

3 Van der Waals势函数排斥项

Slater在考虑了一阶交换力的情况下，计算了间距大于1 Å时的氦原子间排斥势，如方程(6)所示［5］(单位:erg):

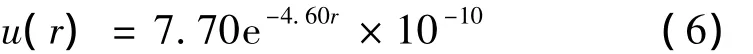
Margenau不同于前人根据热力学参数推导得到描述氦原子的范德瓦尔斯势能曲线(curves for the Van der Waals potential)，而是根据氦的原子结构，提出了用于氦的范德瓦尔斯势能函数排斥项的表达式如方程(7)所示［6］(单位:erg):

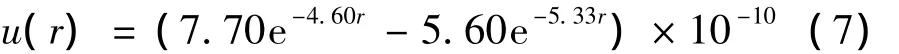
不同于Slater与Margenau的理论计算方法，Amdur利用实验研究手段，通过对分散于氦气中的高速氦原子碰撞截面的研究，提出了可以应用于小间距范围内(0.55 A＜r＜1.05 A)的氦原子排斥势函数形式［7-8］，如方程(8)所示(单位:erg):

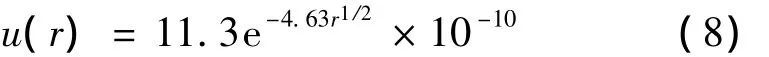
如果采用Kell等人的研究方法处理相同的实验数据，可以得到有效间距在0.52—1.02 Å的氦原子排斥势函数形式，如方程(9)所示(单位:erg):

可见，方程(9)实际上采用的是关于氦原子间距多项式的形式，如果将其写成指数函数形式，则其在数值上接近于方程(10)(单位:erg):

Amdur在考虑了上述方程的数值差异以及随原子间距变化的趋势关系后，得到了在Margenau方程基础上的的修正势函数排斥项，使其可以适用于粒子间距大于0.52 Å，如方程(11)所示(单位:erg):

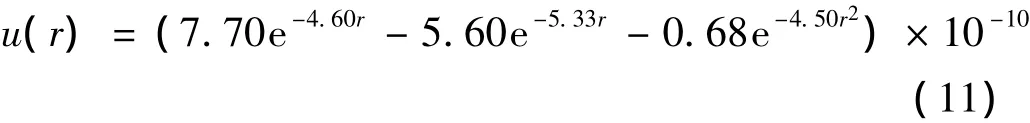
Amdur不断改进实验装置并提高实验精度，给出氦原子排斥势的平均势函数如方程(12)所示(单位:erg)，而其有效的原子中心距为 1.27—1.59 Å［9］。

同时借助于其他研究者发表的势函数排斥项的数值，采用插值的方法，得到了可以应用于1.27—2.30 Å的势函数。方程(6)—方程(12)之间的差异如图4a、图4b、图4c所示。

而Kistemaker与Keesom认为Slater等人提出的排斥势过小，而提出了新的排斥势函数，如方程(13)所示(单位:erg):

由此排斥势构造的EXP-6-8型势函数可以与低温下第二维里系数达到很好的一致性。随后Schneider与Intema提出了可以在高温下与第二维里系数实验值形成较好符合性的势函数，其排斥势形式如方程(14)所示［10］(单位:erg):

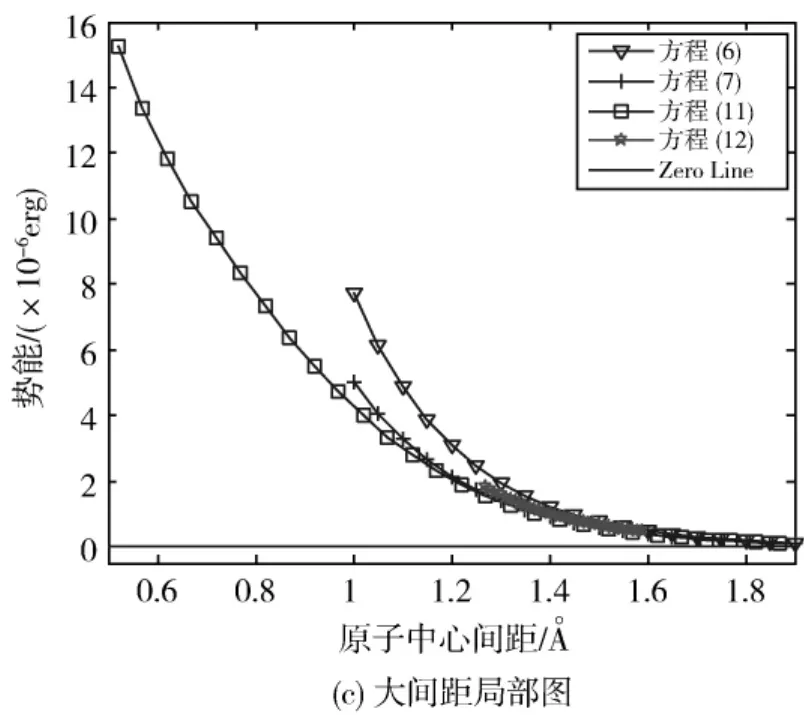
图4 氦的Van der Waals势函数排斥项Fig.4 Repulsive potential of helium

方程(13)、方程(14)与Lennard-Jones势函数排斥项的比较如图5所示。

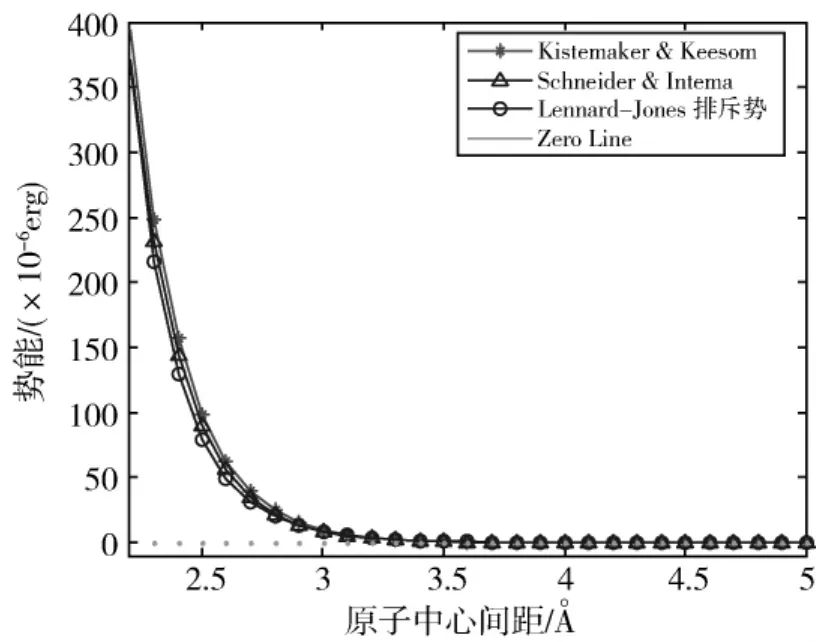
图5 方程(12)、方程(13)与Lennard-Jones势函数排斥项的差异Fig.5 Difference among equation(12)，equation(13)and attractive part of L-J potential

芶清泉等人使用比较准确的解析波函数，严格计算了高温范围内的氦原子间的排斥势，并给出了势函数方程［11］(单位:电子伏，eV):

4 氦原子Van der Waals势函数的拼接构成

根据拼接方程(1)，将Van der Waals势函数写成排斥势与吸引势加和的形式，如表1所示，势函数形式及其与Lennard-Jones势函数的比较如图6所示。

表1 氦原子Van Der Waals势函数形式Table 1 Different Van Der Waals potentials of helium

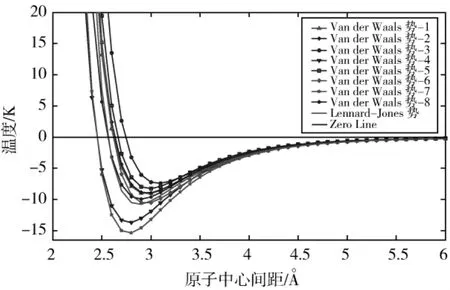
图6 拼接构造Van der Waals势函数Fig.6 Van der Waals potentials obtained by join-up construction

5 结论

由此可见，氦原子势函数可由其范德瓦尔斯排斥势和吸引项拼接构造而成，其通用势函数可写为:

其中:第一项为排斥项，第二项、第三项与第四项分别是由偶极相互作用、偶极-四极相互作用和四极-四极相互作用引起的吸引势。

1 Chester H Page.Van Der Waals forces in helium［J］.Physical Review，1938，53(1):426-430.

2 Henry Margenau.The role of quadrupole forces in Van Der Waals attractions［J］.Physical Review，1931，38(15):747-756.

3 田春玲，刘福生，蔡灵仓，等.采用从头计算方法研究液态氦原子间等效对势［J］. 高压物理学报，2006，20(1):15-19.

4 Slater J C，Kiekwood J C.The Van Der Waals forces in gases［J］.Physical Review，1931，37(15):682-695.

5 Slater J C.The normal state of helium［J］.Physical Review，1928，32(9):349-360.

6 Margenau H.Van der Waals potential in helium［J］.Physical Review，1939，56(15):1000-1008.

7 Amdur I，Pearlman H.Helium repulsive potential from collision cross section measurements［J］.Journal of Chemical Physics，1941，9(6):503-506.

8 Amdur I.Repulsive interaction potentials at small interaction distances:He-He and H-H2 systems［J］.Journal of Chemical Physics，1949，17:844-845.

9 Amdur I，Harkness A L.Scattering of high-velocity neutral particles:II.Helium-Helium［J］.Journal of Chemical Physics，1954，22(4):664-669.

10 Rosen P.The repulsive poential of normal helium atoms［J］.Journal of Chemical Physics，1950，18(9):1182-1186.

11 芶清泉、黄树勋，刘志渊，等.高温氦气中氦原子间的排斥势函数与二级维里系数［J］.成都科技大学学报，1981(1):11-18.

Study on join-up construction of semie-mpirical potentials for helium-4 atoms based on Van der Waals forces

Chen Yu1Chen Shuo2

(1College of Mechanical Engineering，Shanghai University of Engineering Science，Shanghai 201620，China)
(2School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China)

In order to find the general form of potential function for helium-4 atoms in molecular dynamics studies，Van der Waals force of helium was analyzed and it was indicated that the potential function for helium could be constructed based on Van der Waals repulsive forces and attractive forces.General form of potential function for helium atoms was concluded，which indicated that the repulsive part of potential function was not fit for expressing in minus twelve power of r and exponential function form should used instead.This kind of potential was composed of short-range repulsion and long-range attraction.The general form of resulting potentials was composed of repulsive energy expressed in exponential form，the attractive energy resulted from dipole-dipole，dipole-quadrupole and quadrupole-quadrupole interaction respectively，the dipole-dipole molecular interaction was the main part of the Van der Waals attractive forces.

helium;Van der Waals force;potential function;join-up construction

TB611

A

1000-6516(2011)06-0016-05

2011-09-06;

2011-11-03

国家自然科学基金(10872152)项目资助、上海市自然科学基金(10ZR1412700)项目资助。

陈 煜，女，35岁，博士、副教授。