矩形薄板在面内随机参数激励下的随机分岔研究

葛 根，王洪礼，许 佳

(1.天津工业大学 机械学院，天津 300160;2.天津大学 机械学院，天津 300072)

目前薄板在各种工程领域中得到了广泛的应用。在建筑工程、机械工程以及航空航天工程中使用更为常见。由于薄板一般具有较大的柔性，在外界激励的作用下容易发生振动，所以研究薄板的非线性动力学问题就显得尤为重要。国内外众多非线性学科的学者在此方面做了很多工作。张伟等［1－3]利用全局摄动法研究了矩形薄板的全局分岔及混沌现象;杨志安等［4－6]研究了在非线性地基模型支撑的地基薄板的频率响应问题。以上文献的都是使用确定性非线性系统理论进行研究的，而事实上，薄板在实际情况中往往受到随机激励的作用。葛根等［7]研究了具有摩擦边界的矩形薄板在面内随机激励下，一阶模态的随机分岔和稳定性问题。但对薄板高阶模态的随机动力学特性尚无研究。

本文在考虑文献［7] 的研究结论后，建立了四边简支的矩形薄板在含噪声信号的面内激励下的二阶随机参数激励模型，并且发现该随机系统的广义Hamilton函数形式要比文献［7] 中的一阶模态复杂得多，并用拟不可积Hamilton系统随机平均法把薄板振动系统表示为一维Ito扩散过程。随后研究了参数变化对薄板振动时稳定性的影响，得到了系统的随机局部、全局稳定性及分岔条件随系统受参激强度变化的特性。

1 薄板随机振动模型的建立

如图1所示薄板，矩形薄板长宽分别为a和b，厚度为 h，在 x=0，，x=a，y=0，y=b 四边简支。在板中面建立如图1所示的坐标，设 u，v，w 分别为 x，y，z方向的位移。在x=0，，x=a两边受面内激励p(t)，为板中面内的分布载荷，其形式为:p(t)=p0+p'ζ(t)，其中，p0为均布载荷，ζ(t)为0均值，强度为2D的高斯白噪声，p为噪声的幅值。在该薄板可认为是柔性大挠度板。

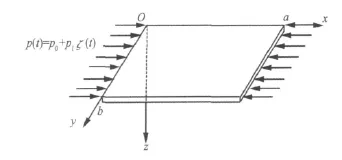
图1 矩形薄板振动模型及坐标Fig.1 The model of a rectangular thin plate and the coordinate system

［2] 及冯－卡曼方程，可建立板的横向振动方程为:

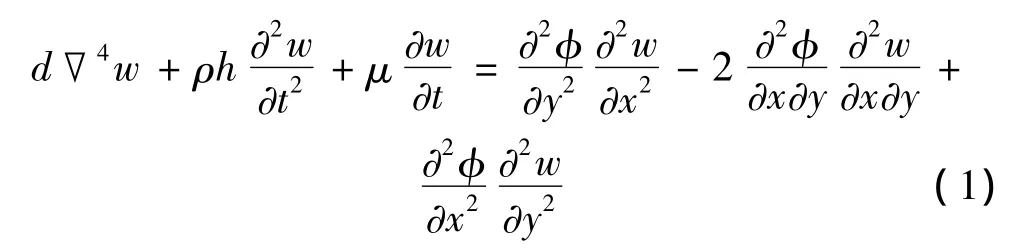
且满足:

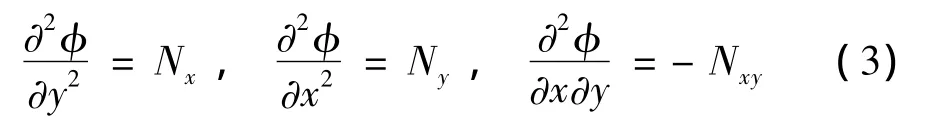
其中:Nx，Ny，Nxy分别为板内各方向的内力。

板的简支边的位移边界条件可表示为:

在 y=0，b处:

力边界条件为:

y=0，b处:

设满足位移边界条件(4)的板的二阶模态为:

代入式(2)，并考虑力边界条件(5)求出板的内力Nx、Ny、Nxy如下:

把内力式(7)、式(8)、式(9)和模态式(6)代入式(1)可得:

根据Galerkin变分法，可求得离散化及参数化简后薄板的常微分形式的模态方程:

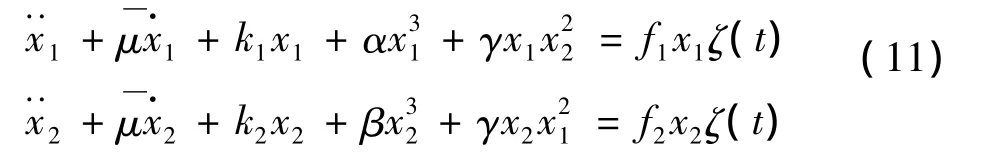
其中参数化简的形式为:

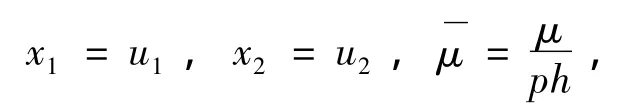
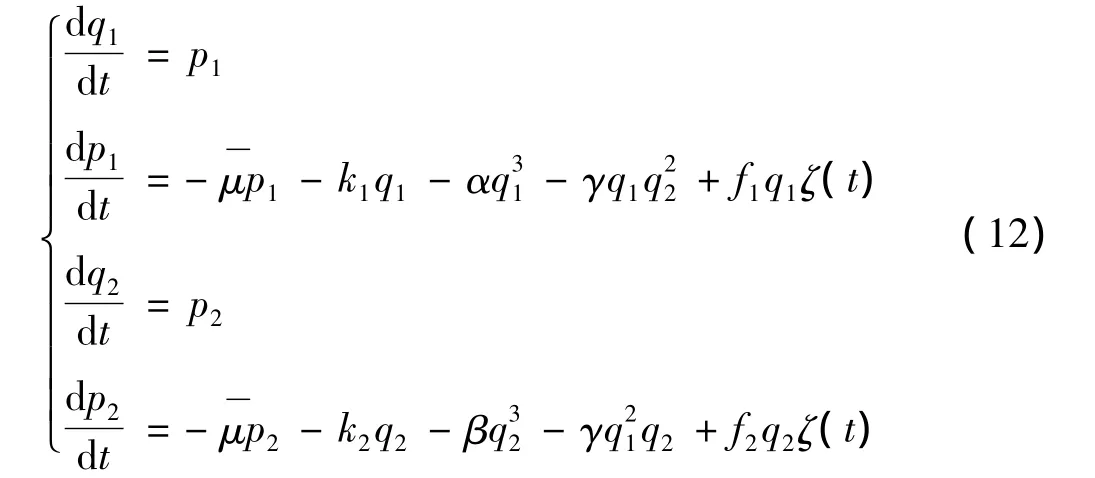
为研究系统(12)在随机激励下系统能量的变化，设系统的Hamilton函数(广义能量)为:，其中:

p，q为广义位移和广义动量。可把系统写为:

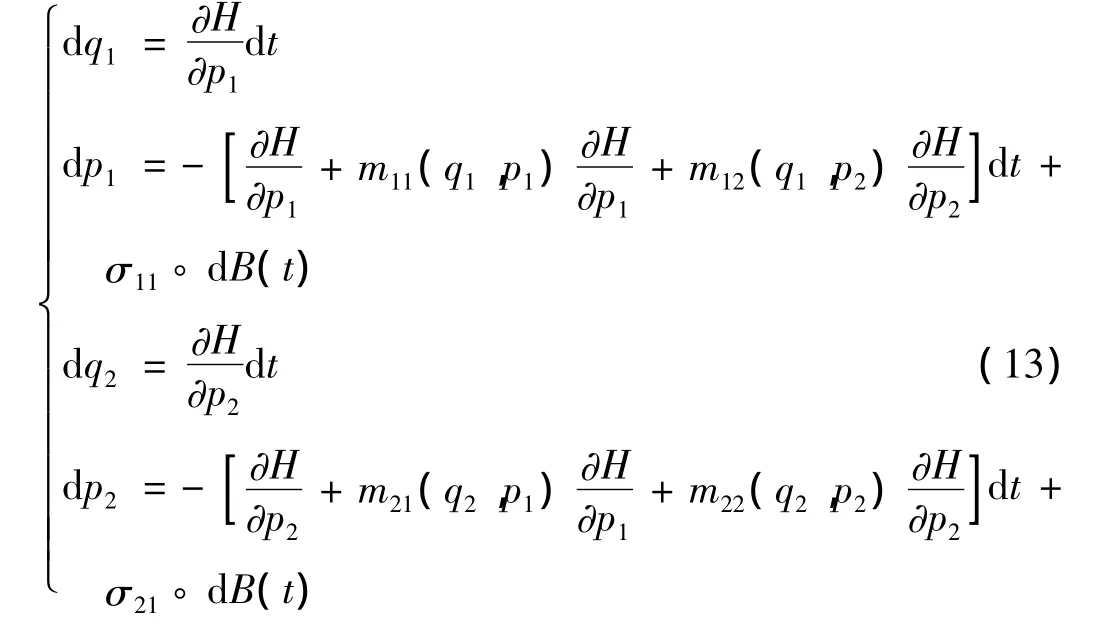
其中:

该Hamilton系统不存在与H(t)独立对合的首次积分，该系统为一个拟不可积Hamilton系统。根据拟不可积Hamilton系统的定义及性质，可知系统(13)依概率收敛到一维Ito扩散过程:

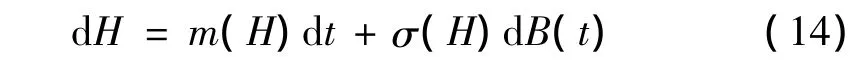
其中，B(t)是标准Weiner过程，m(H)和σ(H)分别是Ito随机过程的漂移系数与扩散系数。使用拟不可积Hamilton系统的随机平均法［8]，得到:

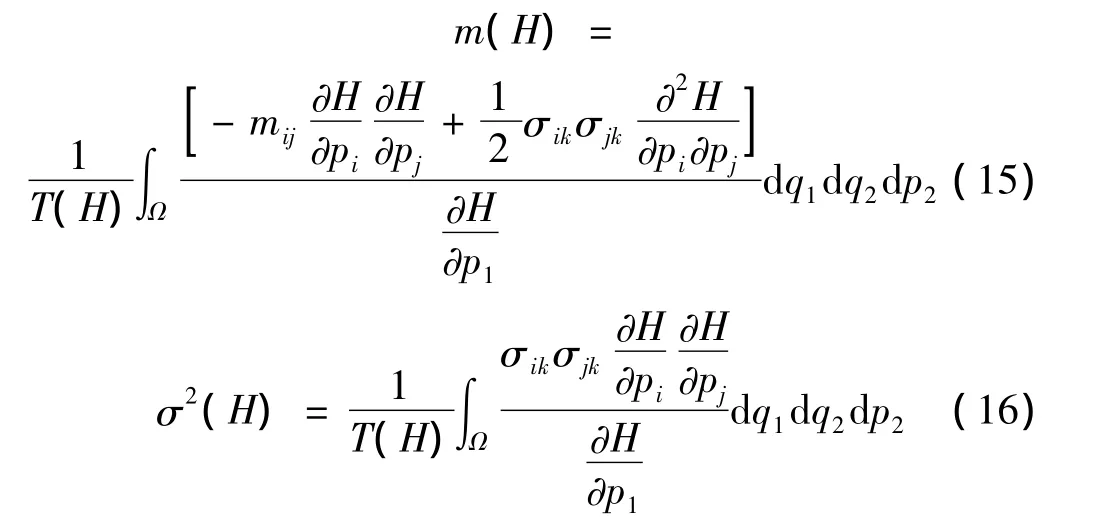
其中:Ω =({q1，q2，p2H(q1，q2，0，p2)≤H)，下标(i，j，k)为约定求和标值。

这里R是方程(21)的根。

2 矩形薄板模型的随机稳定性

2.1 局部稳定性

线性化系统的最大Lyapunov指数定义为:

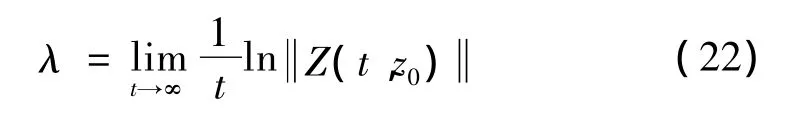
由Oseledec乘积遍历性定理可知，系统(14)平凡解以概率1渐近稳定的充要条件是:最大Lyapunov指数λ＜0。显然，方程(14)只有一个平凡解(0，0)，则平均Ito方程只在零点处取得唯一平凡解，将(14)在H=0处线性化，得到线性化的Ito微分方程:

解得:

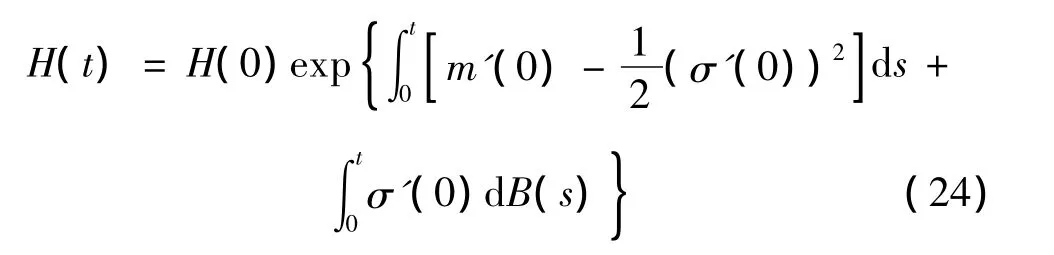
故系统最大Lyapunov指数为:

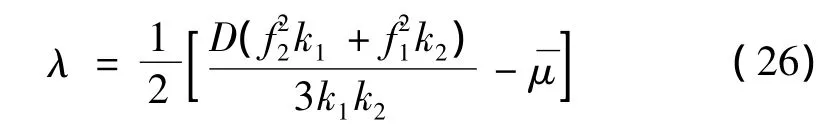
2.2 全局稳定性

通过计算系统最大Lyapunov指数的方法只能用于判定系统的随机局部稳定性，却无法用于系统随机全局稳定性的判定，所以只能采用随机扩散过程的奇异边界理论［10]来判定系统的全局随机稳定性。

一维扩散过程的概率渐近稳定性由该过程在奇异边界上的性态确定，因此下面主要分析扩散过程的两个奇异边界性态:左边界H→0和右边界H→∞。

当H→0时，使 σ2(H)=0，m(H)=0，属于第一类奇异边界，H→0为套点。漂移系数m(H)和扩散系数σ(H)渐近地收敛于下面的两式:

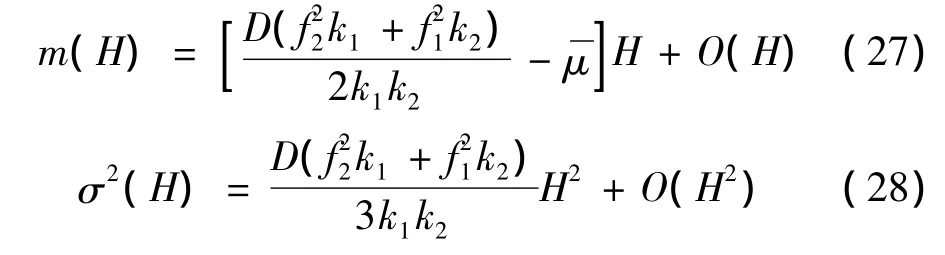
根据参考文献［10] 表2－8.2和表2－8.4的结论奇异边界的划分标准可知，平均Ito方程(12)的左边界属于第一类奇异边界。相应的，判断边界类别的扩散指数αl(下标l表示左边界)、漂移指数βl以及特征标值cl分别为:

当H→∞时，H应对应R的高次项，对式(19)求期望，可知:

把式(30)代入式(19)、式(20)，可知:

且知，在H→∞时，

下面讨论参数对系统全局稳定性的影响，当cl＜1，即满足时，左边界H→∞是吸引自然边界。说明当满足式(26)时，左边界吸引，右边界排斥，系统的解曲线会在整个能量域上向左边界，也就是能量趋向0靠近，所以此时系统是全局稳定的，由此可知满足条件(26)时，系统不但是局部稳定而且是全局稳定的。

图2 特征标值变化对系统全局稳定性影响示意图Fig.2 The global stability conditions with the changing of the character value

可以发现该结论符合一般的常识，当系统的阻尼系数越大时，系统能量耗散越快，系统越趋向稳定;当随机干扰噪声密度D越大，则系统的能量越不易控制。

相反，当cl＞1时，左右边界都是排斥自然边界，系统的解曲线会在整个能量域上往返，其具体的稳态位置需要求解系统的FPK(Fokker-Planck-Kolmogorov)方程方可知。

3 系统的随机分岔

当特征标值cl＞1时，系统在取某能量值处会出现最大的概率密度，对应的物理意义为系统在受随机参数激励时最有可能的能量大小。当参数变化时，系统能量的最大概率密度可能出现Hopf分岔［11]，对应的是系统出现类似确定性系统中“极限环”的现象，振荡变得剧烈，系统可能被破坏。因此有必要通过研究系统的FPK方程，可得到出现Hopf分岔的条件。

系统(12)对应的FPK方程为:

其中f为稳态概率密度函数。

求解方程(30)，得到稳态概率密度:

其中A为归一化常数。

由于这里我们研究的系统能量应在平衡点附近，则考虑忽略式(19)、式(20)中的R4高阶项。代入式(33)中后解得:

其中:

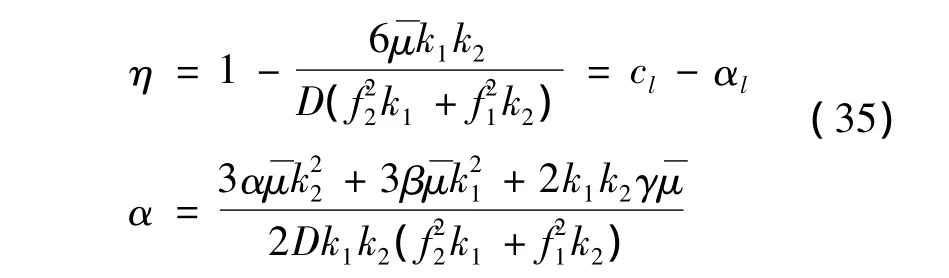
系统广义位移与系统广义动量的联合平稳概率密度表达式为:

则稳态概率密度可改写为:

稳态概率密度函数 f(H)=O(Hη)，且有 η=cl－αl。当满足η＜－1时，稳态概率密度函数在H=0处是一个δ函数;－1＜η＜0，则稳态概率密度函数f(H)是H=0处有最大值的减函数;当η＞0时，稳态概率密度函数f(H)在远离H=0处有峰值。这意味着，在η=－1时发生随机D－分岔(动态分岔，意义类似于确定性系统分岔);在η=0时会发生随机P－分岔(唯像分岔，概率密度函数的形状变化)，这两次分岔构成了随机Hopf分岔。

下面着重讨论η=0处的随机P－分岔，给定参数条件下的系统平稳概率密度f(H)和系统响应联合概率密度 f(q1，q2，p1，p2)随参数变化的数值结果。

由于参数众多，本文选取对控制系统全局稳定性有重要意义的无量纲阻尼系数μ为分岔控制参数。设其它的无量纲参数为:

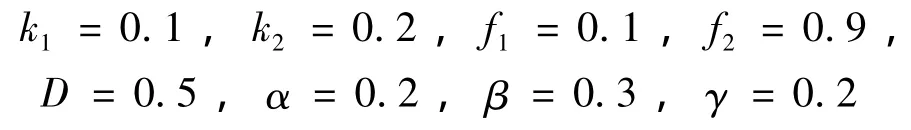
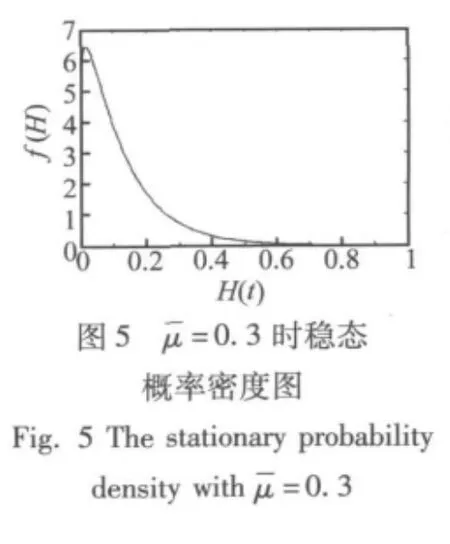
从图3到图6的数值模拟可知，当阻尼系数增大时，系统的稳态概率密度函数的图形形状发生了变化。稳态概率密度函数的峰值的位置表示发生分岔的对应系统广义能量值，峰值的高度代表概率密度的大小。尤其在阻尼参数取值在使η＞0后，根据图5和图6的比较可看出，此时系统发生分岔的能量不在能量H=0处，且随阻尼参数减小，η变大，系统发生分岔的概率最大对应的能量值H也变大，对应的峰值降低。

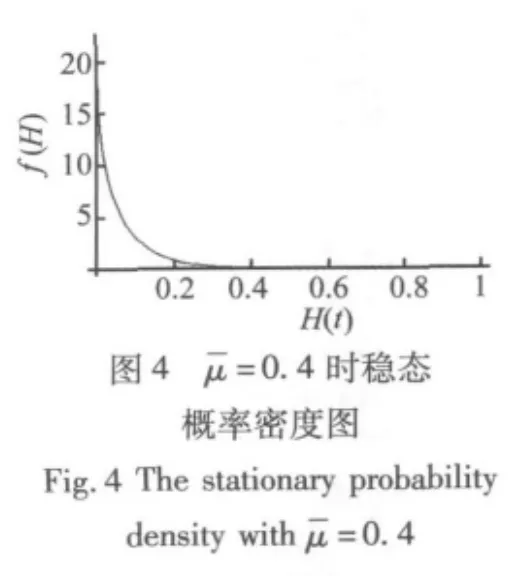
下面对系统的联合概率密度函数做数值模拟。由于系统 Hamilton函数的变量是 q1，q2，p1，p2四个，根据式(36)得出的联合稳态概率密度函数的图形是5维的，不利于显示。所以可以先固定(q2，p2)的值，画联合概率密度函数 f(q1，p1)，设 q2，p2=0.2，0.2，代入式(36)后作数值模拟。

随机系统产生的分岔行为与确定性系统产生的分岔行为是有明显区别的，随机系统由于受到随机因素的作用，系统发生分岔是以概率形式来反映的。一方面，即使满足一定的分岔条件，分岔也并不是一定会发生，发生分岔的概率反映了发生分岔的可能性的大小，可见随机系统的复杂性，因此无法做出对随机分岔的准确的预测;另一方面，系统的参数发生变化时，发生分岔的概率大小也会发生相应的变化，可以通过调节系统参数，尽量降低分岔发生的概率。

通过具体分析，得到了影响系统性态的分岔参数μ，分析了分岔参数取值对随机Hopf分岔的影响。根据研究经验，在稳态概率密度出现火山口时即可判定发生随机Hopf分岔，随机Hopf分岔的产生会导致系统发生类似确定性系统“自激振动”的现象，从而造成系统损坏，为了避免Hopf分岔的产生可通过调节分岔参数使其值远离分岔值，即可降低发生分岔的危险。

4 结论

本文的主要工作为，首先建立了四边简支矩形薄板的受面内随机激励的随机动力学模型，然后用拟不可积Hamilton系统随机平均法将表示系统能量(Hamilton函数)的变化过程简化为一个一维扩散过程。最后利用奇异边界理论和随机分岔理论研究了系统的稳定性和分岔情况。可得出如下结论:

(1)对系统的边界分析得出，当系统的阻尼系数大于一个定值时，左边界吸引右边界排斥，所以系统一定以概率1稳定;当系统的阻尼系数小于一个定值时，左边界排斥，右边界也排斥，系统的解曲线会在能量域上往返。

(2)通过求解系统的稳态概率密度函数，得出了系统发生随机D－分岔的条件即为系统全局稳定的条件。并通过数值模拟研究了系统发生随机P－分岔的条件与现象。

参考文献

［1] Zhang W， Liu Z M， Yu P. Global dynamics of a parametrically and externally excited thin plate.［J] Nonlinear Dynamics，2001，24:245 －268.

［2] Zhang W.Global and Chaotic dynamics for a parametrically excited thin plate.［J] Journal of Sound and vibration，2001，239(5):1013－1036.

［3] Cao D X，Zhang W.Global bifurcations and chaotic dynamics for a string-beam coupled system.［J] .Chaos，Solitons ＆Fractals，2008，37(3):858 －875.

［4] 杨志安，赵雪娟.非线性弹性地基上矩形薄板受双频参数激励作用的非线性振动［J] .应用力学学报，2007，24(3):494－498.

［5] 杨志安，赵雪娟，席晓燕.非线性弹性地基上矩形薄板的非线性振动与奇异性分析［J] .振动与冲击，2006，25(5):69 －73.

［6] 杨志安，赵雪娟，席晓燕.非线性弹性地基上矩形薄板的主参数共振［J] .岩土力学，2005，26(12):1921 －1925.

［7] 葛 根，王洪礼，许 佳.矩形薄板在面内随机参数激励下的随机稳定性与分岔研究［J] .振动与冲击，2009，28(9):91 －94，194.

［8] Zhu W Q，Ying Z G，Soong T T.An optimal nonlinear stochastic control strategy for randomly excited structural systems［J] .Nonlinear Dynamics，2001，24:31 － 51.

［9] Zhu W Q.Lyapunov exponent and stochastic stability of quasi-non-integrable Hamiltonian system［J] .International Journal of Non-Linear Mech，2004，39:569 －579.

［10] Zhu W Q. Nonlinear stochastic dynamics and control:framework of Hamiltonian theory［M] .Beijing:Science Press;2003.

［11] Zhu W Q，Huang Z L.Stochastic Hopf bifurcation of quasinonintegrable Hamilton systems［J] .International Journal of Nonlinear Mechanics，1999，34:437 －447.