索力振动测量的传递矩阵法

刘志军， 芮筱亭， 杨富锋， 于海龙， 姜世平

(南京理工大学 发射动力学研究所，南京 210094)

拉索作为结构的主要承重构件在工程中得到了广泛应用，拉索张力的大小直接关系到结构的受力状况。在工程实践中，常用的索力测定方法有压力表测定法、压力传感器测定法和振动法。前两种方法在测量多根拉索张力过程中需要反复地移动压力表或压力传感器，从测得的固有频率估算索力的振动法因其简单、快速而在拉索张力的测量中常常被采用［1－3]。一般采用微分方程或差分方程描述拉索动力学特性，在此基础上可推导出索力与索振动频率的关系［4－9]，本文应用多体系统传递矩阵法无需建立和求解描述拉索运动的微分方程或差分方程［10]，在建立拉索振动的离散模型基础上得到元件的传递方程及系统总传递方程，然后通过特征方程求解得到拉索固有频率及其变化规律，从而确定了拉索张力与其固有频率之间的关系，对索力计算公式进行了修正，从而完善了拉索张力的振动测试方法;最后结合具体工程实例进行讨论分析。

1 索振动分析的传递矩阵法

图1所示为一段长为L、两端固定的索的横向振动情况。为推导制约此段索振动的运动方程，将此连续系统视为相应的离散系统当自由度无限增加时的极限。

图1 索的横向振动Fig.1 Transverse vibration of the cable

首先，将索的质量集中成为n+2个质点，不妨假设它们等距均布在索的弦线方向上，即有Δx=xi+1－xi(i=0，1，…，n)在振动中保持不变，且这些质点由没有质量只有张力的弦连接起来。第二，假设索做微幅振动，即有各段弦与 x 轴的交角 θi(i=0，1，2，…，n)很小，因而有如图1所示建立惯性直角坐标系，系统中无质量弦为铰元件，质点为体元件，由n+2个集中质量和n+1个无质量弦组成简单链式离散系统，系统的元件个数为2n+3，各元件只在y轴方向振动，左端为系统输入端，右端为系统输出端，从左至右为传递方向，依次对元件编号，输入端边界编号为0，输出端边界编号为2n+3。假设Pij表示连接点，其中第1个下标i是体元件的序号，第2个下标j是铰元件的序 号。定 义 状 态 矢 量 Z0，1、Z2，1、Z2，3、Z4，3、……、Z2n，2n－1、Z2n，2n+1和 Z2n+2，2n+1的形式均为 Z=［Y，Θ]T。

1.1 质点的传递矩阵

质点的传递矩阵表示该点的左、右侧面的状态矢量传递关系的传递矩阵。体元件质点i的受力如图2所示。

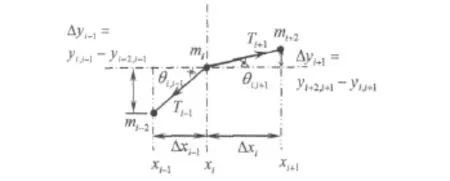
图2 质点i受力图Fig.2 The free-body diagram of the particle

图2 所示横向振动系统中的集中质量mi的左侧和右侧位移相等，即:

由Newton定律得:

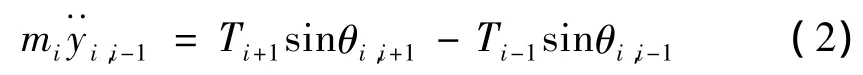
因拉索作微幅振动，假设各处张力相等，对简谐振动集中质量mi有传递方程:

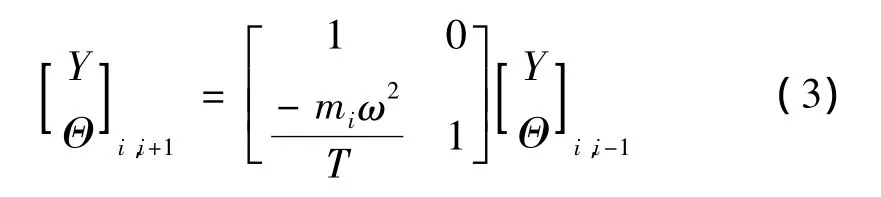
即:

式中:

1.2 无质量弦的传递矩阵

无质量弦的传递矩阵是表示其左、右侧面的状态矢量传递关系的传递矩阵。铰元件无质量弦i的受力如图3所示。

图3所示横向振动系统中的无质量弦在输入点和输出点与x轴的夹角相等，即:

图3 无质量弦受力图Fig.3 The free-body diagram for the chord of negligible weight

由于索作微幅振动而各段弦与x轴的夹角很小，因此:

对简谐振动无质量弦有传递方程:

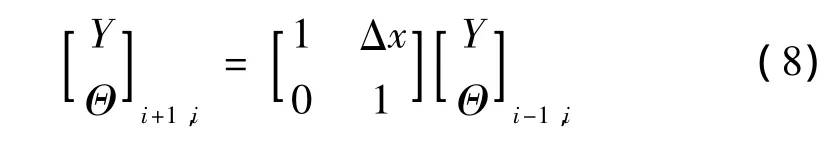
即:

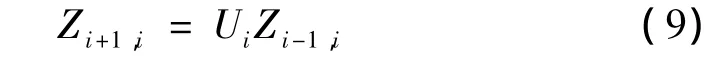
式中:

1.3 特征方程

元件的传递方程为:

系统总传递方程为:

将边界条件

代入上式得:

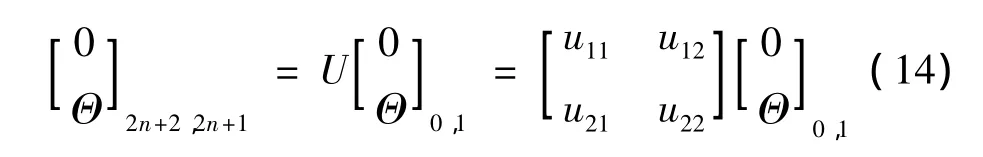
解得特征方程

求解上式可得系统 n个固有频率 ωk(k=1，2，3，…，n)。对每一个 ωk，取 Θ0，1=1，求解各个元件传递方程可得系统的全部状态矢量，进而可得系统振型为:

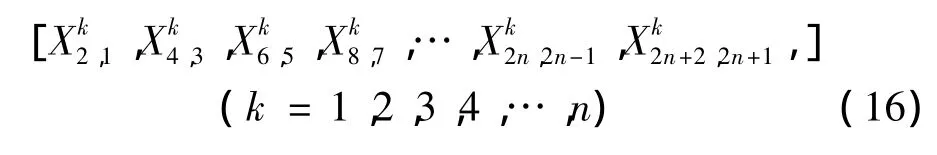
2 拉索自振频率测试及内力分析

拉索张力振动测量一般是将加速度传感器固定在拉索上并拾取拉索在环境随机激励或人工激励下的振动信号，经过滤波、放大、模数转换、谱分析，根据频谱图来确定拉索的自振频率，然后由拉索自振频率与索力的关系来确定其张力，它属于间接测量拉索张力的方法。

图4 a 拉索振动固有频率计算流程 图4b 拉索张力测量流程Fig.4(a)Flow diagram for nature frequencies computation(b)Flow diagram for the cable tension measurement

由式(15)可知，特征方程求解得到的拉索自振频率与张力是对应的，即已知拉索张力大小，可以计算出对应的拉索各阶自振频率，反过来，若已知拉索若干阶自振频率，也可以确定拉索张力大小，拉索振动固有频率计算流程如图4(a)所示。首先计算出实测结果频谱图中相邻两谐振峰之间频率差Δfn=fn+1－fn，依据低阶频差的平均值估计基频^f1，然后应用传递矩阵法对拉索进行振动分析，求解特征方程(15)得到拉索在初始计算张力值下的固有频率及其变化规律，依此确定拉索振动信号频谱图中各峰值对应的自振频率阶数。将计算得到的模态频率与测试得到的模态频率比较，当两者相差较大时，按一定比例(1% ～10%)增大或减小拉索计算张力值，重新应用传递矩阵法进行拉索振动分析，求解特征方程(15)得到拉索的自振频率，直到计算得到的频率与测试得到的频率值相差最小时为止，此时即可确定拉索实际张力值T0，应用多体系统传递矩阵法进行拉索张力振动测量流程如图4(b)所示。

3 实例分析

以武汉白沙洲长江大桥2号墩边跨上游C17号索为测试对象，其主要参数为:索长L=228.802 4 m，弹性模量 E=1.95 ×105MPa，横截面积 A=5.349 3 ×10－3m2，单位长索质量 m=43.9 kg/m，索的倾斜角度α=33.962 6°;图5和图6分别为C17号斜拉索在初张拉后实测所得振动信号及其功率谱图。

从图6可以看出，由于C17斜拉索较长且传感器安装在其桥面端附近，只得到了斜拉索较高阶的自振频率。采用高阶频率多阶差平均的办法［3，11]计算得=0.307 8 Hz，使用本文提出的方法计算得到拉索张力 T 为 1 264.1 kN，实测值 T为 1 255.4 kN21.006 8，满足工程要求。

4 结论

(1)应用传递矩阵法对拉索进行振动分析无需建立和求解描述其运动的微分方程或差分方程，而基于弦振动理论的索力振动测量方法采用微分方程或差分方程描述拉索动力学特性。

(2)应用传递矩阵法对拉索进行振动分析涉及的系统矩阵阶次不取决于系统的自由度数，仅取决于元件的最高矩阵阶次，使矩阵阶次比有限元等方法的矩阵阶次低得多，计算量小得多，计算速度快得多。

(3)传递矩阵法具有结构矩阵分析的优点，可直接调用已推导的元件传递矩阵，建模灵活，程式化程度高，从而非常便于实际应用。

(4)通过对实际工程的测试结果分析表明，索力振动测量的传递矩阵法具有准确、实用和易编程的特点，完全能满足工程应用要求。

［1] Russell J C，Lardner T J.Experimental determination of frequencies and tension for elastic cables［J] .Journal of Engineering Mechanics，ASCE，1998，124:1067 －1072.

［2] Cunha A，Caetano E，Delgado R.Dynamic test on large cable-stayed bridge［J] .Journal of Bridge Engineering，ASCE，2001，6(1):54 －62.

［3] 刘志军，陈国平，党志杰.检测斜拉索张力的振动法及其应用［J] .南京航空航天大学学报，2006，38(5):609－612.

［4] Irvine H M.Cable structures［M] .London:The Mit Press，1981.

［5] Takahashi K，Konishi Y.Non-linear vibrations of cables in three dimensions，partⅠ:non-linear free vibrations［J] .Journal of Sound and Vibrations，1987，118(1):69 －84.

［6] Warnitchai P，Fujino Y，Susumpow T.A non-linear dynamic model for cables and its application to a cable-structure system［J] . Journal of Sound and Vibrations， 1995，187(4):695－712.

［7] Mehrabi A B，Tabatabai H A.Unified finite difference formulation for free vibration of cables［J] .Journal of Structural Engineering， ASCE， 1998， 124(11):1313－1322.

［8] 任伟新，陈 刚.由基频计算拉索拉力的实用公式［J] .土木工程学报，2005(11):26－31.

［9] Zui H，Shinke T，Namita Y.Practical formulas for estimation of cable tension by vibration method［J] .Journal of Structural Engineering，1996，122(6):651－656.

［10] 芮筱亭，贠来峰，陆毓琪，等.多体系统传递矩阵法及其应用［M] .北京:科学出版社，2008.

［11] Ren WX，Liu H L，Chen G.Determination of cable tensions based on frequency differences［J] . Engineering Computation-An International Journal for Computer-Aided Engineering and Software，2008，125(2):172－189.