基于主分量子空间的设备状态诊断研究
2011-09-17刘永斌何清波孔凡让
刘永斌,何清波,吴 强,李 鹏,胡 飞,孔凡让
(中国科学技术大学 精密机械与精密仪器系,合肥 230026)
机械设备如齿轮箱、轴承、发动机等在工业应用中扮演着非常重要的角色。设备状态诊断可以及时有效地辨识设备状态,减少设备停机,保证设备高效运行。振动信号蕴含着丰富的设备状态信息,适合于提取可靠的特征进行状态识别[1]。目前振动信号的时域、频域和时频域特征提取技术得到了很大发展,研究者总希望提取更多的有效特征参数进行故障分类和诊断。但是采用特征参数太多会影响模式分类的计算代价甚至分类精度[2]。而且它们所反映的状态规律性、敏感性,和模式聚类性、可分性并不相同,在特征分析基础上提取规律性好、敏感性强的特征表示非常需要且极具挑战性[2,3]。
主分量分析(Principal component analysis,PCA)是一种通用的多元统计方法,在信息压缩和数据相关性消除方面非常有效,被广泛用于人脸、字符等特征提取中[4,5]。PCA的这些优点也被引入设备状态监测与诊断中。Malhi[2]基于PCA提出一种特征抽取方案以保证从多个原始特征中选择最有效的特征来进行轴承状态分类。Baydar[6]运用基于PCA的多元统计方法建立了一个正常状态模型进行齿轮箱状态监测。He[7]探讨了设备状态监测中主分量特征的有效选取。同时,子空间法模式识别也具有很多优点,它可以将特征提取和模式分类两步合在一步内完成,计算方便快捷[8]。本文结合PCA和子空间法研究基于主分量子空间的设备状态诊断,探讨两种主分量子空间结构来表达和分类设备的状态。在齿轮箱诊断应用的实验表明,所提出的设备状态诊断方法非常有效,且计算方便。
1 PCA特征提取
PCA的基本思想是寻找高维数据的一些主分量表示,这些分量具有最大方差,用它们表示原始数据具有最小的均方误差。
设有模式向量矩阵X,其列向量xi为某一状态样本对应的d维模式向量,则可以得到该矩阵的协方差矩阵为:
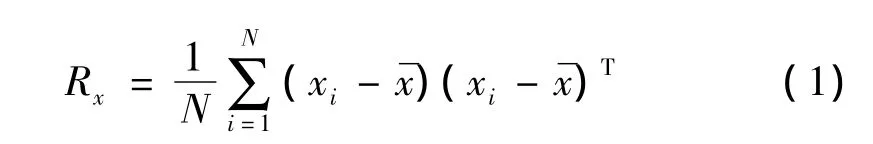
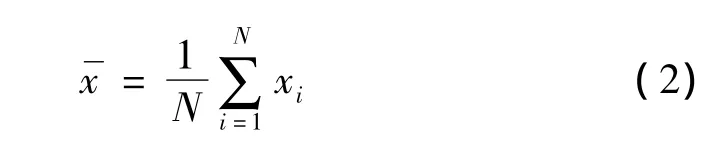
对RX做特征值分析,通过求解下式:

其中λ和v分别是RX的特征值和特征向量,得到d个特征值 λi(i=1,2,…,d),且 λ1>λ2>… > λd,以及对应的特征向量vi(i=1,2,…,d)。样本x投影到特征向量vi上得到相应的主分量特征:

模式向量X投影到所有特征向量张成的d维正交空间得到d维主分量特征。原始数据的绝大部分信息通常保留在前面少数几个主分量中,因而可以仅用m(m<d)个特征向量组成一个正交特征子空间。该特征子空间相比原始模式空间具有降维的优势,可以近似表示原始数据结构,且不会影响分类的精度。
2 主分量子空间结构
子空间可以看作是由一些特征矢量作为坐标轴的模式点集。子空间法模式识别被广泛应用于语音[8]、人脸[9]、字符[10]、系统辨识[11]等模式识别研究中。下面探讨两种用于设备状态监测和诊断的主分量子空间结构。
2.1 压缩子空间结构
用原始模式空间中包含所有类别的样本训练来构造的子空间称为压缩子空间。该结构压缩了样本集的绝大部分变化信息,表达了类别之间的本质区别,不同类别的样本形成一个聚类并占据着子空间中不同的区域。
设训练模式矩阵X中的d维模式向量xi分属于q个类别j=1,…,q},则对于样本集1,…,N}(ci表示模式 xi的类别),其模式均值为:
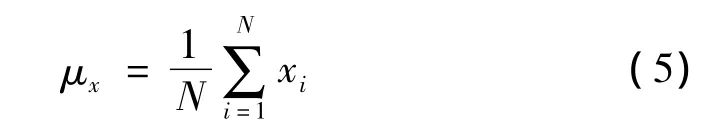
协方差矩阵为:
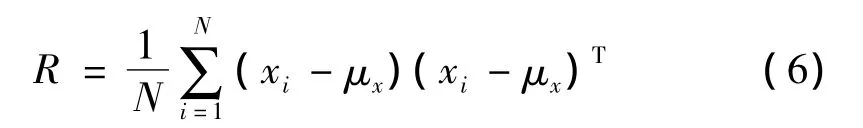
其中N是训练样本数。通过(3)式求得R的特征值和特征向量。主特征矢量表示为i=1,…,m}(m<d),作为坐标轴展开子空间,样本投影到特征矢量上得到相应的主分量特征。这种PCA特征记作PCA1。同类别样本的PCA1特征具有一定的聚类特性,每种状态类的聚类中心采用模糊c均值聚类分析[10](FCMC)来计算。这些聚类中心用于输入测试样本的分类。
测试时,模式x首先投影到训练好的压缩子空间上得到其PCA1特征表示,然后计算它与各类别之间的相似度。相似度用下面的余弦距离来测量:

其中Ftest和Ftrain分别是测试样本和训练类中心的PCA1特征,测试模式被分到具有最大相似度的类。
2.2 类属子空间结构
用每类训练样本分别建立一个子空间,对某个类别的子空间,该类样本分布在子空间原点附近形成聚类,其它类样本则会偏离原点,且分布聚类性和规律性也没有保障,故称其为类属子空间结构。
同样对上述训练模式矩阵X,摘取类Cj的样本集i=1,…,Nj}(ci表示模式 xi的类别,Nj是该类样本数),则Cj类属子空间可以由下面的协方差矩阵得到:
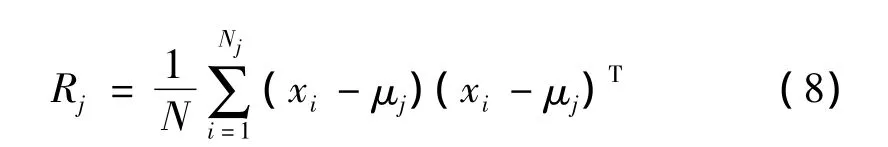
其中:

是Cj类属模式均值。通过(3)式求得Rj的特征值和特征向量。选取m(m<d)个主特征矢量i=1,…,m},反映了Cj类数据的分布规律,用来作为该类属子空间的坐标轴系。把样本投影到某类属子空间主特征矢量上得到该子空间的主分量特征,记作PCA2。
测试时,样本x依次投影到训练好的每个类属子空间上,得到其PCA2特征表示,然后分别计算在每个子空间上的投影距离:

由于属于某类的样本与该类通常距离很小,而不属于该类的样本则与该类距离较大,测试模式被分到具有最小投影距离的类。
3 实例分析
采用某汽车变速齿轮箱为研究对象获得振动数据,振动信号由安装在三档齿轮箱外壳上的加速度传感器获取,经放大后,由A/D卡采集并存储到计算机,采样频率为3 000 Hz。设定转速为1 600 r/min,三档齿轮的啮合频率经计算为500 Hz。施加负载255 N·m,对该齿轮箱进行了疲劳试验,共进行了六个循环,三档齿轮经过了正常、轻微磨损、严重磨损并发生断齿故障。分别抽取齿轮正常、轻微磨损和严重磨损阶段振动信号各80组进行分析,其中50组用于训练,30组用于测试。样本集与其所属的齿轮状态的对比关系见表1所示。

表1 样本与齿轮状态的对应关系Tab.1 Corresponding relations between samples and gearbox conditions
3.1 振动信号模式特征
齿轮箱振动是一种复杂的随机过程,很难用确定的时间函数表达,对其状态监测和诊断时需要进行特征分析,提取能够反映状态信息的模式特征。较常用且有效的特征是时域和频域的统计特征。
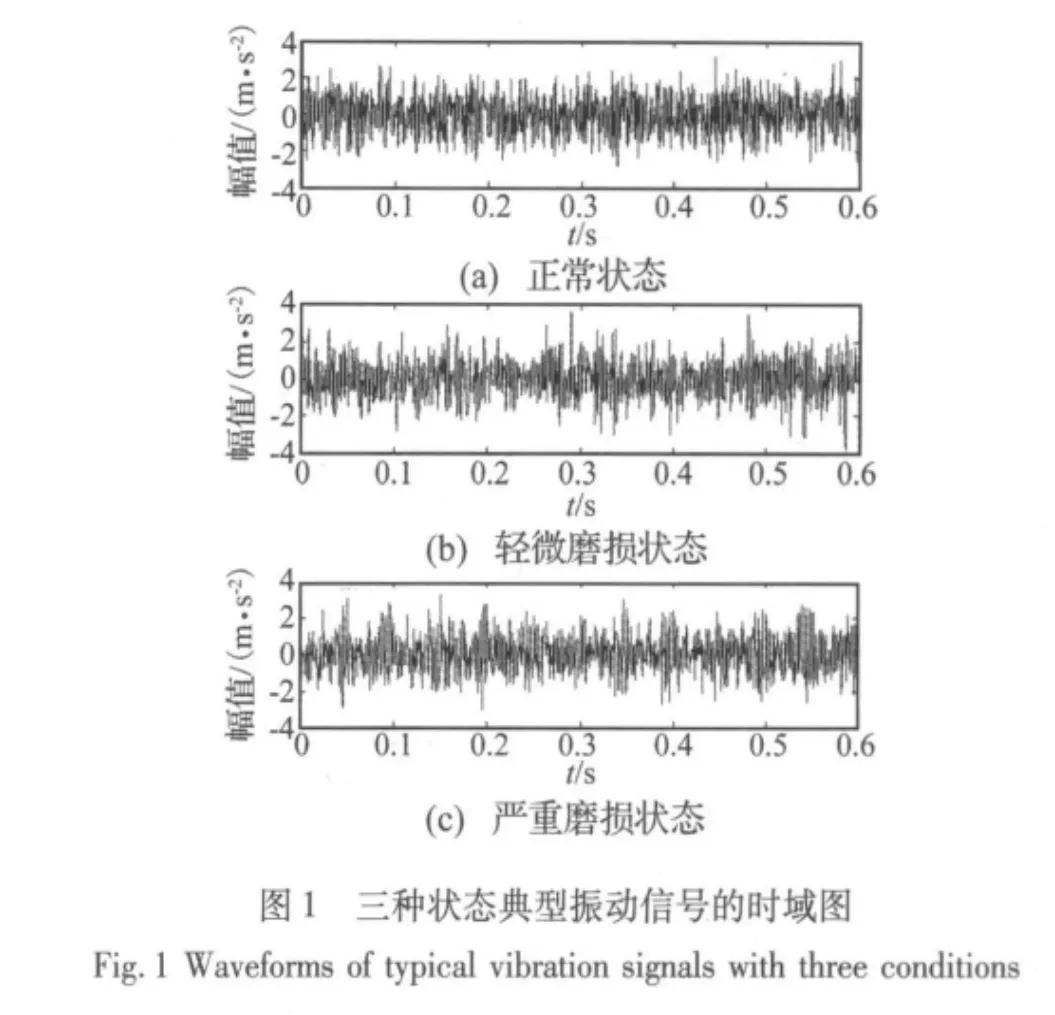
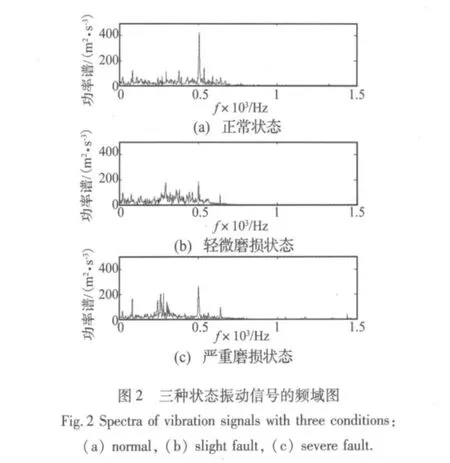
为了消除操作环境及传感器因素对数据的影响,使信号分析结果有一个客观、公正的标准,对所测振动信号进行了均值—方差标准化预处理。预处理后的信号具有零均值和单位方差。三种齿轮状态的典型振动信号如图1所示,从图中并看不出它们之间的区别。而从图2所示的频率图上来看,齿轮啮合频率500 Hz附近的能量反映状态差异的规律不明显,250 Hz~300 Hz附近的能量分布则呈现出逐步递增的趋势。频谱上的变化可以在一定程度上反映出不同阶段磨损的特征。
据以上分析,本文提取振动信号的时域和频域统计特征来全面表达齿轮状态的模式特征。①时域统计特征。因为标准化后的时域信号对不同状态的反映不明显,首先采用非平稳信号分析工具小波包变换来对280 Hz所在的小波包系数进行重构,以消减背景噪声、得到敏感的状态特征信息。然后提取绝对均值、最大峰值、有效值、方根幅值、方差、峭度、峰值因子、波形因子、脉冲因子、裕度因子等10个时域统计参数[1]。②频域统计特征。均值—方差标准化的信号变换到频域,分成8个频带分别计算各频带的功率谱能量。在频域提取各频带的功率谱能量以及它们的均值、频率重心、谱方差、谱峰、谱峭度等13个统计特征[3]。这样总共提取出23个特征指标表示振动信号的模式特征。这些特征表达齿轮状态的规律性和敏感性都不相同,同时也具有一定的冗余性。主分量子空间技术正是从这些原始特征中消除相关和冗余、提取更加敏感和稳定的特征来表达齿轮箱状态。
3.2 状态诊断:应用主分量压缩子空间法
如前所述,用含三种状态的所有训练样本来建立一个压缩子空间。为了使结果可视化,我们提取了两维子空间结构,用对应两个最大特征值的特征向量来展开。计算显示,这两个特征值占有了所有特征值的83.3%比例。所有训练样本投影到该子空间上得到两维PCA1特征,如图3(a)所示。可以看出,每个类都有明显的聚类,并占据了子空间的不同的区域。这显示了PCA具有优越的特征提取能力,用压缩子空间法提取的子空间很好地表达了各个状态的本质特征。
用FCMC技术计算对应三个状态的聚类均值,如图3(a)所示。三个聚类中心有效表示了三个状态类别的均值,可以代表每个类用于测试样本的状态分类。
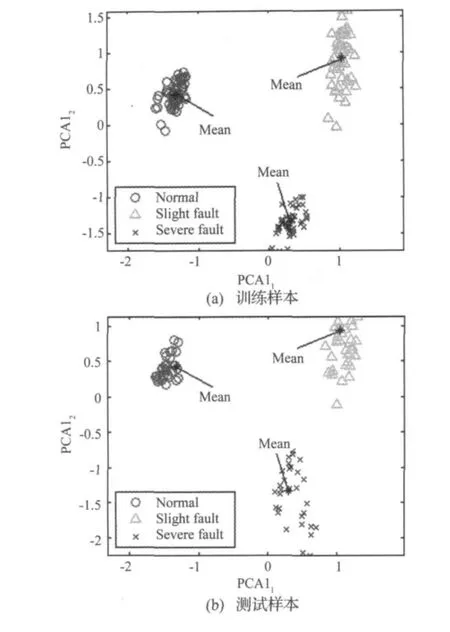
图3 训练样本和测试样本分别在两维压缩子空间上的投影Fig.3 Projection on two-dimensional compression subspace of(a)training and(b)testing samples
现在用已得到的子空间来监测测试样本的状态。首先测试样本用训练样本的均值和方差进行标定,然后投影到建立好的子空间上,得到两维PCA1特征表示,如图3(b)所示。图中的三个均值与图3(a)的相同,从图3(b)中可见,不同状态测试样本的投影分别聚集在相应的三个状态的均值附近,这说明了PCA1子空间对类别表达的有效性。
下面用余弦距离来计算测试样本与三个聚类中心的相似度,图4是结果的柱状图表示。从图4中可见,正常状态样本与正常状态类别的余弦相似度最大,其它两类样本也都与各自类别的余弦相似度最大,而且它们的值都接近为1,其它情况的余弦值基本都是负的。经过诊断,测试样本得到了正确的分类结果,所以压缩子空间可以非常有效的用于齿轮状态的识别和分类中。
3.3 状态诊断:应用主分量类属子空间法
如前所述,分别用每种状态的训练样本来建立一个该类别的类属子空间。对每个状态类都提取了两维子空间结构,用对应两个最大特征值的特征向量来展开。所有训练样本投影到每个子空间上得到其两维PCA2特征,如图5左侧所示。从图中可以看到,每个状态的类属子空间中,该状态样本都聚集在子空间原点附近,两维特征均具有零均值;其它两类则没有这样的性质。这说明类属子空间可以有效表达类别的特征。
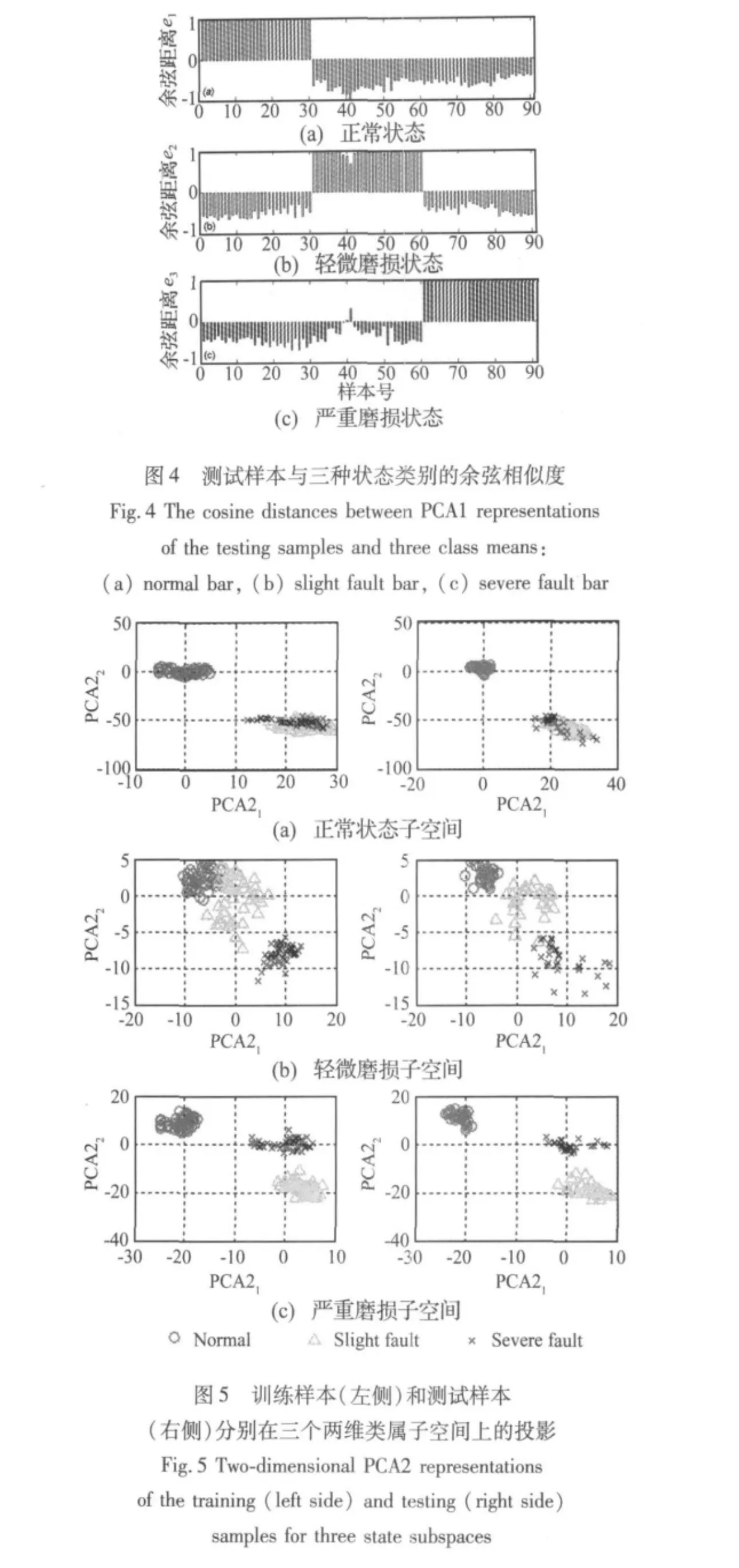
用上面得到的三个类属子空间来诊断测试样本的状态。首先测试样本分别用每个子空间所属类的训练样本的均值和方差进行标定,然后投影到该子空间上得到两维PCA2特征表示,如图5右侧所示。从图5中可见,测试样本和训练样本在每个子空间都有着一致的分布。这说明了PCA2子空间对类别表达的有效性。
用类属子空间上的投影距离进一步诊断测试样本的类别。图6是测试样本在各个子空间上的投影距离的柱状图表示,从中可以看出,每个状态类样本都与各自类别子空间的投影距离最小,而且它们的值都比较稳定,其它情况的投影距离则都较大。根据投影距离越小相似度越大的准则,测试样本得到了正确的分类结果,所以类属子空间也可以非常有效地用于齿轮状态诊断中。
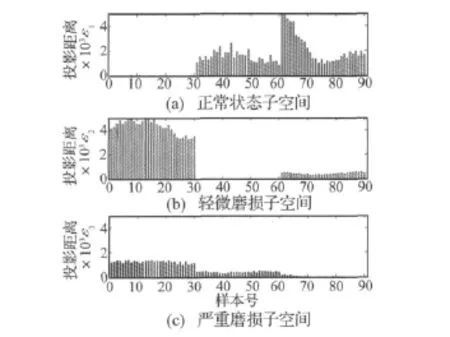
图6 测试样本与三个类属子空间的投影距离Fig.6 Projection distances of testing samples onto three class-specific subspaces
4 结论
本文结合PCA和子空间法研究了基于主分量子空间的设备状态诊断,探讨了压缩子空间和类属子空间两种主分量子空间结构来表达和分类设备的状态。所提出的设备状态诊断方法具有两个优点:①能够提取稳定有效的设备状态低维特征表示,②能够以低代价有效进行状态监测和诊断。针对某一汽车变速齿轮箱的实例分析表明,两种主分量子空间法都获得了良好的结果,可以有效用于齿轮箱的状态诊断中。两种方法比较起来,压缩子空间的训练代价比类属子空间大。当监测中增加类别数时,前者需要重新对所有样本进行训练,而后者只需要对新类别的样本数据来训练一个新的子空间。所以类属子空间比较适合动态的状态监测与诊断。本文方法具有一定的通用性,也适用于轴承等其它部件或噪声等其它采集信号的状态诊断中。
[1] 陈克兴,李川奇.设备状态监测与故障诊断技术[M] .北京:科学技术出版社,1991.
[2] Malhi A,Gao R.PCA-based feature selection scheme for machine defect classification[J] .IEEE Transactions on Instrumentation and Measurement,2004,53:1517 -1525.
[3] 温熙森,胡茑庆,邱 静.模式识别与状态监控[M] .长沙:国防科技大学出版社,1997.
[4] JolliHe I J.Principal component analysis[M] .Springer,New York,1986.
[5] Turk M,Pentland A.Face recognition using eigenfaces[C] .Proc.IEEE Conf.on Comp.Vision and Patt.Recog.,1991,586-591.
[6] Baydar N,Chen Q,Ball A,et al.Detection of incipient tooth defect in hhelical gears using multivariate statistics[J] .Mechanical Systems and Signal Processing, 2001, 15:303-321.
[7] He Q,Yan R,Kong F,et al.Machine condition monitoring using principal component representations[J] .Mechanical Systems and Signal Processing,2009,23(2):446-466.
[8] Oja E.Subspace methods of pattern recognition[M] .Research Studies Press,UK,1983.
[9] Franco A,Lumini A,Maio D,et al.An enhanced subspace method for face recognition[J] .Pattern Recognition Letters,2006,27:76-84.
[10] Liu C L,Sako H.Class-specific feature polynomial classifier for pattern classification and its application to handwritten numeral recognition [J] .Pattern Recognition,2006,39:669-681.
[11] 杨 春,欧进萍.子空间系统辨识方法的系统阶数估计[J] .振动与冲击,2009,28(11):13-16.
