一类稠密图色性的刻画❋

詹福琴,乔友付,罗美金

(河池学院 数学系,广西 宜州 546300)

0 引 言

本文仅考虑有限、无向的简单图[1].p(G,λ)表示图 G的色多项式.对于图 G和 H,如果 P(G,x)=P(H,x),称 G和 H色等价,简记为 H～G.[G]表示图 G的色等价图类.称图 G是色唯一的,如果[G]={G}.文献 [2]定义了具有 p个顶点的图 G的伴随多项式为其中 bi(G)表示 G恰有 p-i个分支的理想子图的个数.如果 h(G,x)=h(H,x),称两个图 G和 H是伴随等价的,简记为 H～hG.用 [G]h表示图 G的伴随等价图类.称图 G是色唯一的,如果 [G]h={G}.文献 [3]证明了图 G色唯一当且仅当其补图伴随唯一;G～ H当且仅当文献 [3-7]利用伴随多项式的代数性质研究了许多色唯一图,但对大量非色唯一图的色等价刻画有待研究.本文完整刻画了一类稠密图的色性.

1 预备知识

设 G是一个图,V(G),E(G),p(G),q(G)和分别表示图 G的顶点集,边集,顶点数,边数和补图.G∪ H表示 G和 H不相交的并图,kG表示 k个 G不相交的并图.NG(v)表示图 G中与顶点 v相邻的点集[8].U(G)表示图 G的伴随多项式 h(G,x)的最小实数根.∂(h(G,x))表示伴随多项式h(G,x)的次数.为方便叙述,令 h(G)=h(G,x),h(a,b,c)=h(T(a,b,c),x),h(a,b,c,d,e)=h(T(a,b,c,d,e),x);U(a,b,c),U(a,b,c,d,e)分别表示 h(a,b,c)和 h(a,b,c,d,e)的最小实数根.

Pn和 Cn分别表示 n个顶点的路和圈.Dn表示把 K3的1个顶点和 Pn-2的1个 1度点重叠后得到的图.Fn表示把 K3的 1个顶点与 Dn-2的 1度点重叠后得到的图.

对具有 n个顶点且度序列为(1,1,1,2,2,...,2,3)的树称为 T-形树,记为 Tn(l1,l2,l3),或简记为T(l1,l2,l3).树 T(a,b,c,d,e)表示从 Pc+1的 2个 1度点分别引出两条长为 a,b和 c,d的路得到的图.

Cm(Pn)表示 Cm的 1个顶点和 Pn的 1个 1度点重叠后得到的图.特别地,把 Cm(P2)记作 An.C3(Pm,Pn)表示 K3的 2个顶点分别与路 Pm和 Pn的 1个 1度点重叠后得到的图.C3(T(a,b,c))表示 K3的 1个顶点和 T(a,b,c)的长为 a的路的 1度点重叠后得到的图.特别地,把 C3(T(a,1,1))记作 Bn.

文中所提到的j,a,Y图簇定义如下：

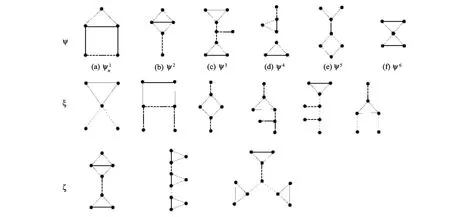
图1 j,a,Y图簇Fig.1 Kinds of g raphs j,a,Y

定义 1[3]对任意图 G,R1(G)称为图 G的第一特征标,定义为

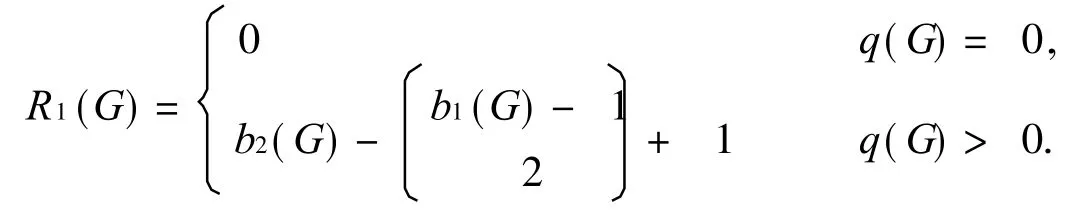
引理 1[3]设图 G的 k个分支分别为 G1,G2,…,Gk,则有

引理 2[9]设 G是 n阶连通图,则

1)R1(G)≤1,等号成立当且仅当 G∈ {Pn,K3,|n≥2};

2)R1(G)=0当且仅当 G∈ {K1,Cn,Dn,T(l1,l2,l3)|n≥4,li≥1,i=1,2,3};

3)R1(G)=-1当且仅当 G∈ {Ca(Pb),C3(T(l1,l2,l3)),Fv,C3(Pm,Pn),T(l1,l2,l3,l4,l5),K-4|a≥4,b≥ 2,v≥ 6,n≥ m≥ 2,li≥ 1,i=1,2,3,4,5};

4)R1(G)=-2,那么 q(G)≤p(G)+2,等号成立当且仅当 G≅K4;

5)R1(G)=-3,q(G)=p(G)+2,当且仅当 G∈Y.

定义 2[10]图 G的顶点序列 x1,x2,...,xk,若满足：

1)除 x1与 xk有可能相等外,其余 xi互不相同;

2)顶点度 d(xi)满足：d(x1)≥3,d(x2)=…=d(xk-1)=2(除非 k=2的情形),d(xk)≥3;

3)对于 i=1,2,… ,k-1,有 xi与 xi+1相邻,则称 x1,x2,… ,xk是图 G的一条内部路.

用 Un表示 Pn-4的两端分别与一条 P3路的 2度点重叠得到的图,即树 T(1,1,n-5,1,1).令 Gx,y表示在图 G的边 xy上增加 1个新顶点得到的图,即图 G的剖分图.

引理 3[11]设 uv是树 G的任意一条边,则

1)若 uv不属于图 G的内部路,则 U(Gu,v)＜U(G);

2)若 uv属于图 G的内部路且 G≠Un,则 U(Gu,v)＞U(G).

引理 4[12]1)h(K3)|h(Fn)⇔n≡ 2(mod 5);

2)h(F5k+2)=h2(K3)Ak(x)+h(K3)xkhk-2(P3)h(P2)[(k-1)xh(P2)+ 2h(P3)],这里 Ak(x)是关于x的有理系数多项式;

3)h(Pn)|h(Fm)⇔ n=2,m=3k+2,或 n=4,m=5k+2.

4)h(Fn)=x[h(Fn-1)+h(Fn-2)],(n≥8).

引理 5[13]设 k≥0,用 G(-k)表示图中所有特征标为 -k的分支的并,Sk表示 G(-k)的分支数,那么

1)当 k=0,1,2时,q(G(-k))-p(G(-k))≤kSk,等式成立当且仅当 G(-k)中的每一个分支均满足 qp=k;

2)当k=3时,q(G(-3))-p(G(-3))≤2S3,等式成立当且仅当 G(-3)中的每一个分支均满足q-p=2;

3)当 k≥4时,q(G(-k))-p(G(-k))＜(k-1)Sk.

引理 6[14]设图 G至少含有 3个 3度点或1个 4度点,并且 G不是树,则U(G)＜-(2+ 5).

引理 7[15]1)当 n≥2时,h(Pn)|h(Pm)当且仅当(n+1)|(m+1);

2)(h1(Cn),h1(P2m))=1,(n＞ 3,m≥1).

引理 8[16]设 f1(x),f2(x),f3(x)是首项系数为正的实系数一元多项式,且

1)f3(x)=f2(x)+ f1(x);

2)f3(x)和 f1(x)次数的奇偶性相反;

3)f1(x)和 f2(x)均有实根,且 U2＜U1.

那么,f3(x)必有实数根且 U3＜U2,这里 Ui表示 fi(x)(i=1,2,3)的最小实数根.

设 C={Cn|n≥ 4},D={Dn|n≥ 4},T0={T0n|Tn(1,1,n-3),n≥ 4},T1= {T1n|Tn(1,l1,l2),2≤ l2≤l3},T2= {|Tn(l1,l2,l3),2≤ l1≤ l2≤ l3},T3=T0∪ T1∪ T2. 有时记

引理 9[17]设,这里 Gi∈ C∪ D∪ T3,令 mi=|E(Gi)|,1≤i≤k,Aj={Gi|Gi∈ Tj}(j=1,2),B={Gi|Gi∈ D-{D4}},Y={Gi|Gi∈ T4(1,1,1)}, 令 t(D)=|B|,t(Tj)=|Aj|,(j=1,2),t(T4)=|Y|,,则

1)bi(G)=bi(Cm),(0≤ i≤ 2);

2)b3(G)=b3(Cm)+t(D)+t(T1)+ 2t(T2)-t(T4).

引理 10[18]设 mi≥3且 mi≠4,则是色唯一的.

引理 11[12]只有当 n=17时,K3与才有可能同时作为 Fn的分支.

引理 12[12]对于 Y型图,有 U(Ym)＜U(Fn).

引理 13[19-20]设 G是一个连通图,则 -(2+)≤U(G)＜-4当且仅当 G是下列图之一：

1)T(a,b,c),其中 a=1,b=2,c＞ 5或 a=1,b＞ 2,c＞ 3或 a=b=2,c＞ 2或 a=2,b=c=3;

2)T(1,a,b,c,1),其中(a,b,c)∈ {(1,1,2),(2,4,2),(2,5,3),(3,7,3),(3,8,4)}或 a≥ 1,b≥b*(a,c),c≥ 1,这里(a,c)≠(1,1)且

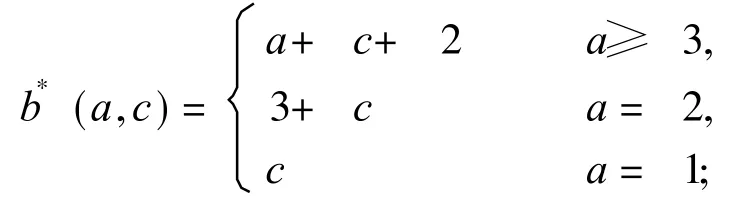
3)Dn(n≥ 9), 或 Fn(n≥ 9),或 G≅Ca(P2)(a≥ 5);

4)C3(1,b,c),其中 b≥ 1,c=1;或 b≥ 4,c=2; 或 b≥c+3,,c≥ 3; 或 C3(1,5,3);

5)C4(P3)或C3(P2,P3).

2 主要结果及证明

证明 当 n≥13时,设 h(G)=h(Fn).因为

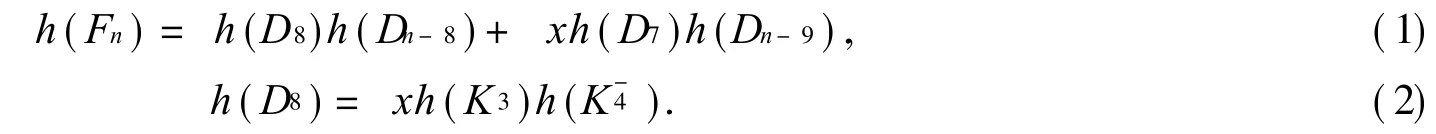
若 n-9≥ 10,则 h(Dn-9)=h(D8)h(Pn-17)+xh(D7)h(Pn-18),故 h1()|h(Pn-18),但 U(Pn-18)＞-4.而 U()=-4,矛盾.故 n-9≤ 9,即 n≤ 18.

由引理 4知 h(Fn)=x(h(Fn-1)+h(Fn-2)),再由递推可得

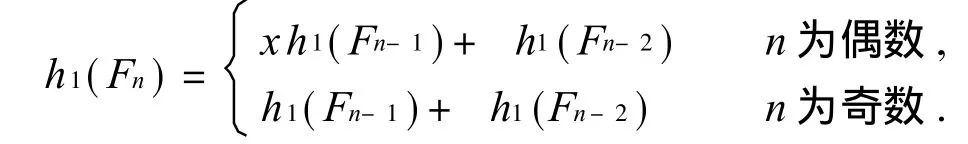
计算(文中所说的计算均由 Mathematica4.0计算所得)知 h(F6)=x2(x4+ 7x3+13x2+ 7x+1),h(F7)=x3(x4+ 8x3+18x2+14x+3).所以,当 n=2k+1(k≥3)时,h1(Fn)的最低项系数 bn=k;当 n=2k(k≥3)时,h1(Fn)的最低项系数 bn=1.由于 h1(K-4)=x2(x+ 1)(x+ 4)=x2(x2+ 5x+ 4).所以,当n≤ 18且 n≠ 9,17时 ,h1(K4-)|/h(Fn).

计算知 h(F9)=x4(x5+ 10x4+ 34x3+ 46x2+ 24x+ 4),h(F17)=x8(x+ 1)(x+ 4)(x2+ 6x+ 1)(x2+4x+ 2)(x3+6x2+8x+1).验证可得 h1(K-4)|/h(F9),h1(K-4)|h(F17),而已知 n≠17.

故结论成立.

定理 1 设 G=∪ Cui∪ Fn,A={ui|ui≥ 4的正整数},E4={ui|ui∈ A,ui=4},则 [G]h={G}如下：

证明 设 h(H)= h(G)= h(∪ Cui∪ Fn)=h(Cui)h(Fn).由引理 4得 h1(K3)|h(F5k+2),h12(K3)|/h(F5k+2),h1(P4)=h1(K3).由 h1(P4)不可约及引理 7知(∏h1(Cui),h1(K3))= 1.因此,H中至多含有一个 K3分支.

设 H=∪ Hi,Hi是 H的分支.H中特征标为 -k的所有分支的并为 H(-k),H(-k)中的分支个数为Sk(k≥0).H中各分支的最小特征标为 -k0,则

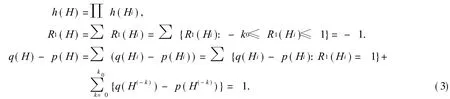
设图 H中 K3分支个数为 i(0≤i≤1)个,由引理 2知,图 H中路分支数为因此

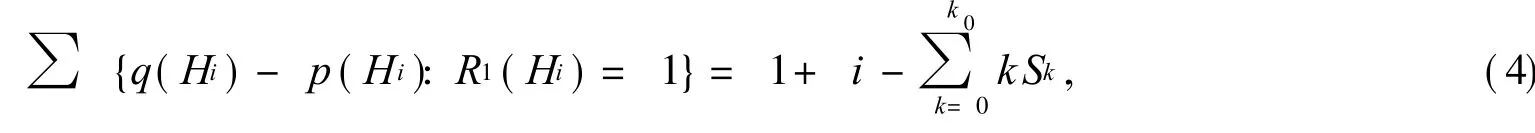
由式(3),式(4)得

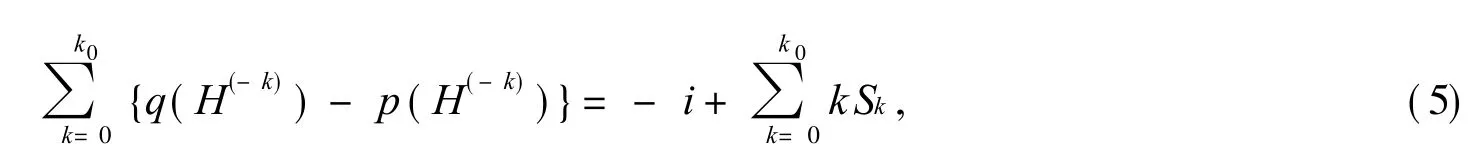
由引理 5得

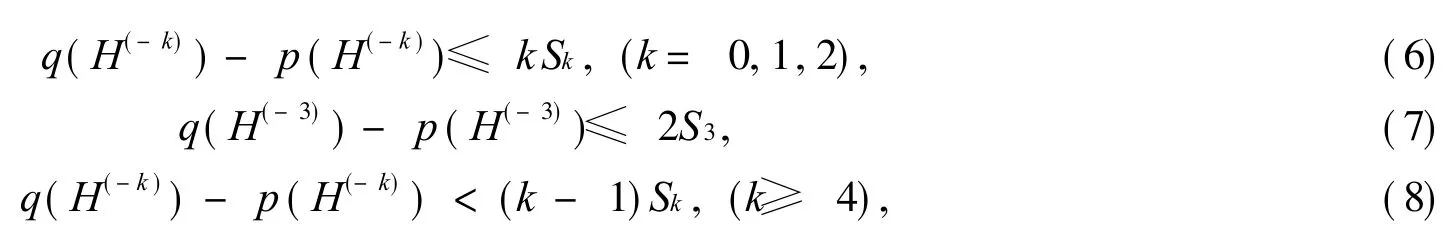
从式(5)～(8)可得

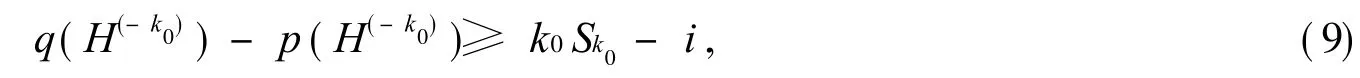
因此,H(-k0)中至少存在一个分支 Hi满足 q(Hi)-p(Hi)≥k0-1.

下面对 k0分情况讨论：

情形 1 当 k0≥4时,由式(8),式(9)得 k0Sk0-i≤q(H(-k0))-p(H(-k0))＜(k0-1)Sk0.而 0≤i≤1,所以该情形不存在.

情形 2 当 k0=3时,则 3S3- i≤ q(H(-k0))- p(H(-k0))≤ 2S3,此时,只有 S3=1,i= 1.从而H(-3)中只有一个分支 H1,满足由引理 2和引理 12知 U(am)＜U(Fn).所以,该情形不存在.

情形 3 当 k0=2时,则 2S2-i≤ q(H(-2))- p(H(-2))≤ 2S2.

情形 3.1 当 i=0时,则 q(H(-2))- p(H(-2))= 2S2.H(-2)的分支均满足 q(Hi)-p(Hi)=2.由引理 2的(4)得 Hi≅K4.由 h(K4)=x4+6x3+7x2+x,验证知 U(K4)＜-4.4.由 h(F6)=x6+7x5+13x4+ 7x3+ x2,可得 U(F6)＞ -4.4.

由引理 3知 U(Fn)＜U(Fn+1),所以U(K4)＜U(F6)≤U(Fn).从而,U(K4)＜U(Fn).所以,该情形也不存在.

情形 3.2 当 i=1时,则 q(H(-2))- p(H(-2))= 2S2- 1,从而 H(-2)恰有一个分支 H1,满足q(H1)-p(H1)=1,其余满足 q(Hi)-p(Hi)=2.由引理 2知 H1∈ j,其它分支 Hi≅K4(i≥2).

由引理 6知j2,j3,j4,j5,j6不可能是 H的分支.而对j1由计算知

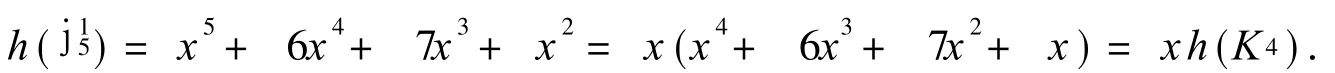
情形 4 当 k0=1时,则 S1-i≤ q(H(-1))- p(H(-1))≤ S1.

情形 4.1 当 i=0时,则 q(H(-1))- p(H(-1))= S1.所以,H(-1)中的分支 Hi均满足 q(H(-1))-p(H(-1))=1.由引理 2知 Hi∈ {Fm,结合式(5),q(H(0))-p(H(0))=0.因此,H(0)的分支只能是阶数大于 3的 Cmi或 Dn.再由引理 14,引理 11可得 Hi≇K4-.

从而只有 Hi≅Fm,故 S1=1,路分支数为 0.所以,H=Fm∪(∪ ACmi)∪(∪ BDni),mi∈ A,ni∈ B.A={mi|mi≥ 3},B={ni|ni≥ 4}.从而,h1(H)= h1(Fm)∏h1(Cmi)∏h1(Dni).比较两边最小根,因U(Fn)＜U(Fn+1),所以,m=n.从而h1(Cui)=∏ih1(Cmi)∏h1(Dni),

根据引理 9,比较等式两边第四项系数 b3,可得 ni=4或 B=j.

由引理 10得 ,H=Fn∪(∪ Cui)∪(T C4∪ U D4).T+U=|E4|,ui≠ 4.

情形 4.2 当 i=1时,则 S1- 1≤ q(H(-1))- p(H(-1))≤ S1.

情形 4.2.1 当 q(H(-1))-p(H(-1))=S1时,H(-1)的分支均为 Fm和 K4-.这时路分支为 S1-2,即S1≥2.但)|/h1(Fn),矛盾.因此,这种情形也不存在.

情形 4.2.2 当 q(H(-1))-p(H(-1))=S1-1时,H(-1)中有一个分支 H1,满足 q(H(-1)1 )-p(H(-1))=0,其余分支 Hi满足 q()-p()=1.由式(5)可推得 q(H(0))-p(H(0))=0.从而,由引理 2可得

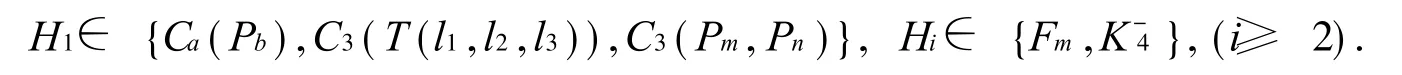
若 Hi≅Fm,因为 U(H)=U(G)＜U(Fm),由引理 3知 U(Fn)=U(Fn+1).又知 H中含有 K3,从而可得m ＜n,且有 U(左 )＞ U(右 ).所以 Hi≇Fm,从而 Hi≅.

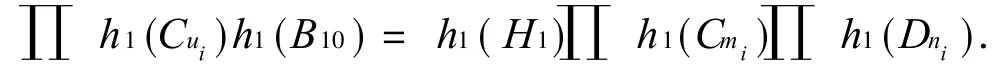
比较最小根得 U(B10)=U(H1).又因为 H1∈ {Ca(Pb),C3(T(l1,l2,l3)),C3(Pm,Pn)},所以 H1∈{C5(P2),B10}.

若 H1≅C5(P2),因为 h1(B10)=h1(C4)h1(C5(P2)).所以,

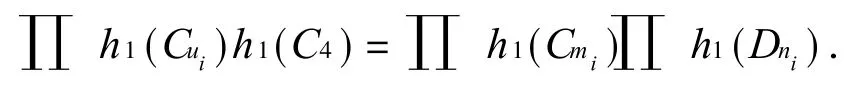
比较两边最小根得U(D4)=U(C4).所以,ni=4.

故 H=K3∪∪ C5(P2)∪(∪ Cui)∪ T C4∪ U D4.T+U=|E4|+1.

情形 5 当 k0=0时,因为 R1(H)=-1,所以,k0≥1.从而此情形不存在.

综合以上讨论可得定理成立.

证明 由定理 1可得结论成立.

[1]王建锋,王静,冶成福.稠密图J].Journal of Southwest University(Natural Science Edition),2009,31(4)：16-20.(in chinese)

[2]Bondy J A,Murty U S R.Graph Theory with Applications[M].North Holland：Amsterdam,1976.

[3]Liu R Y.Adjoint polynomials and chromatically unique graph[J].Discrete Mathematics,1997,172：85-92.

[4]Liu R Y,Zhao L C.A new method for proving chromatic uniqueness of graphs[J].Discrete Mathematics,1997,171：169-177.的色唯一性 [J].西南大学学报(自然科学版),2009,31(4)：16-20.Wang Jianfeng,Wang Jing,Ye Chengfu.The chromatic uniqueness of the dense graph[

[5]Zhao H X,Li X L,Zhang S G,et al.On the minimum real roots of thee-polynomials and chromatic uniqueness of graphs[J].Discrete Math,2004,281：277-294.

[6]Li N Z,Bao X W,Liu R Y.Chromatic uniqueness of the complements of certain forests[J].Discrete Mathematics,1997,172：79-84.

[7]Liu R Y,Zhao H X,Ye C F.A complete solution to a conjectureon chromatic uniqueness of complete tripartite graphs[J].Discrete Mathematics,2004,289：175-179.

[8]孙晓玲,杜建伟.一类外平面图的邻点可区别全染色[J].中北大学学报(自然科学版),2009,30(1)：1-4.Sun Xiaoling,Du Jianwei.Adjacent vertex distinguishing total coloring of a class of outerplane graphs[J].North University of China(Natural Science Edition),2009,30(1)：1-4.(in Chinese)

[9]杜清晏.图的参数 π(G)及其图的分类[J].内蒙古大学学报(自然科学版),1995,26(3)：285-262.Du Qingyan.On the parameter π(G)of graph G and graph classification[J]. Acta Scientiarum Naturalium Universitatis Neimongol,1995,26(3)：285-262.(in Chinese)

[10]Cvetkovic D,Rowlinson P.The largest eigenvalue of a graph：a survey[J].Lin.Multilin.Alg.1990,28： 3-33.

[11]任海珍,刘儒英.R(G)≥-1的图簇伴随多项式最小根极值的刻画[J].数学研究与评论 ,2006,26(4)：819-824.Ren Haizhen,Liu Ruying.On extremes of minimum real roots of adjoint polynomials of graphs with R(G)≥-1[J].Journal of Mathematical Research and Exposition,2006,26(4)：819-824.(in Chinese)

[12]火博丰,王力工,刘儒英.关于图 Fn补图伴随多项式根的讨论和相关结果[J].青海师范大学学报(自然科学版),2005(3)：1-5.Huo Bofeng,Wang Ligong,Liu Ruying.Some important results and discussion about the roots of the adjoint polynomial of the complements of Fn[J].Journal of Qinghai Normal University(Natural Science Edition),2005(3)：1-5.(in Chinese)

[13]火博丰.图的三个参数 A(G),R(G)及 D2(G)的关系 [J].青海师范大学学报(自然科学版),1998,2：1-6.Huo bofeng.Relations between three parameters A(G),R(G)and D2(G)of Graph G[J].Journal of Qinghai Normal University(Natural Science Edition),1998,2：1-6.(in Chinese)

[14]Cevkoic D,Doob M,Gutman I.On graphs whose spectral radius does not exceed(2+)1/2[J].Ars Combin,1982,14：225-239.

[15]赵海兴,刘儒英.不可约路的充要条件 [J].东北师范大学学报(自然科学版),2001,33(2)：18-21.Zhao Haixing,Liu Ruying.The necessary and sufficient condition of the irreducible paths[J].Journal of Northeast Normal University(Natural Science Edition),2001,33(2)：18-21.(in Chinese)

[17]王力工,刘儒英.一类树并的补图的色唯一性 [J].纯粹数学和应用数学,2001,2：126-132.Wang Ligong,Liu Ruying.On the chromatic uniqueness for the complement of the union of the irreducible t-shape trees[J].Pure and Applied Mathematics,2001,2：126-132.(in Chinese)

[18]Du Q.Chromaticity of the complements of paths and cycles[J].Discrete Math,1996,162：109-125.

[19]Zhao H X,Liu R Y.On the minimum real roots of the adjoint polynomial of a graph[J].Discrete Mathematics,2009,309：4635-4641.

[20]Zhao H X,Li X L,Liu R Y.On problems and conjectures on adjointly equivalent graphs[J].Discrete Mathematics,2005,295：203-212.