油田企业科技进步贡献率测算模型的构建

肖贤玉，杜吉家

(1.武汉理工大学管理学院，湖北 武汉 430070;2.武汉理工大学保密办公室，湖北 武汉 430070;3.胜利油田经济开发研究院，山东 东营 257001)

生产科技水平的提高，使一定数量的生产要素组合能够得到高于原先的产出水平，而通常用科技进步贡献率来描述科技进步对经济增长的影响，即科技进步对经济增长的贡献份额［1］。在影响经济增长的诸因素中，剔除增加资金和增加劳动力数量因素以后的部分即科技进步的因素。科技进步对经济增长的作用，是经济意义上的广义科技进步，是综合要素，是基于当今科技进步已渗透到各个方面的理论和简化计算的考虑。

能源开发与利用是一个国家及地区发展的重要基础和保障，石油作为不可再生资源，其开发成本与开发效率至关重要。笔者期望通过对油田企业科技进步贡献率的测算研究，提供一种能准确评价油田企业科技贡献现状的方法，辅助油田做出在科技、资本和劳动等方面的统筹决策安排，最终实现能源的高质量、高效率与低成本的开发。

1 基本理论

1.1 油田企业科技进步贡献率的内涵

早在1928年美国经济学家、数学家柯布和道格拉斯将其研究成果运用于对美国经济增长因素贡献情况的分析。他们在继承和发展前人研究成果的基础上，得出产出主要是资本、技术和劳动力等要素综合作用的结果［2］。基于此，笔者认为，油田企业科技进步贡献率是指油田生产开发过程中，技术研发、应用及改进等技术要素对油田经济产出的贡献程度。科技进步贡献率是相对于资本与劳动贡献率而言的，一般认为这3个方面要素实现了油田经济增长的全部贡献。

影响油田企业科技进步贡献率的主要因素包括:装备技术水平，生产工艺水平，生产作业者素质，管理决策水平。上述4个因素的技术水平越高，则油田企业科技进步贡献率越高，因此，当油田企业处于技术贡献率较低的时期，应主要从装备、工艺、生产者素质及管理水平等方面入手，进行科技创新与改革。

1.2 油田企业科技进步贡献率测算的准则

(1)余值准则。在测算过程中，首先假定油田总产出为技术、劳动以及资本3要素的函数，由于技术最难以量化，因此从总产出中扣除资本及劳动的增长带来总产出的增长部分，用油田产出增长余值来度量其科技进步贡献率。

(2)应用准则。油田在国民经济中的重要地位要求研究成果应用范围较广，并具有较强的适用性［3］。因此，油田企业技术进步贡献率测算应充分考虑油田的主要生产及投入产出指标，尽量构建贴近油田企业的具体生产函数，进而使测算模型更加适用、普遍和准确［4］。

(3)操作原则。测算方法应具有较强的可操作性，在充分、准确地反映油田科技进步的经济意义的同时，尽可能让其计算过程相对简单，易学易懂，十分简便，有利于在较广的范围内推广应用。

2 科技进步贡献率测算模型构建

2.1 索洛余值法

索洛余值法由索洛于1957年首先提出，是目前国内外科技进步测算中最常用的方法［5-7］。索洛余值法认为经济增长所需的各种投入要素，可以聚集为资金K和劳动力L，而最终用K和L这两个最有影响的因素来反映经济产出，并设定生产函数的一般形式为:

由于索洛余值法假设技术进步为希克斯中性，因此式(1)可以表示为:

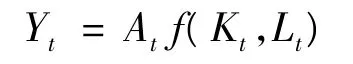
两边取对数，再同时对t求导数，并变形得:

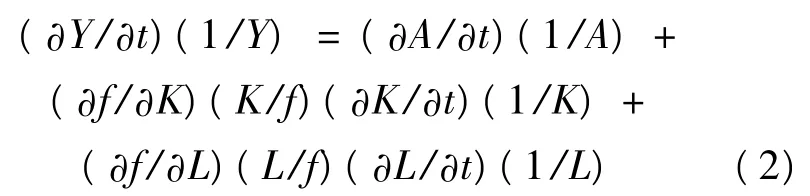
令 α =(∂f/∂K)(K/f)，β =(∂f/∂L)(L/f)，α与β分别为资本和劳动的产出弹性系数，即资本与劳动对经济增长的贡献份额。同时，再令y=(∂Y/∂t)(1/Y)，a=(∂A/∂t)(1/A)，k=(∂K/∂t)(1/K)，l=(∂L/∂t)(1/L)，则式(2)可变为:

式(3)即著名的索洛余值计算科技进步的年平均增长速度的数学模型，则科技进步的年平均增长速度a用余值法表示为:

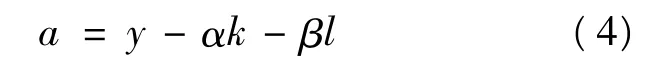
式中:y为产出量的增长速度;k为资本投入量的增长速度;l为劳动力投入量的增长速度;α为资本产出弹性系数，其他条件不变的情况下，资金增加1%，产出增加α%;β为劳动力的产出弹性系数，其他条件不变的情况下，劳动力增加1%，产出增加β%。

而科技贡献率Ea则是科技进步增长速度与经济产出增长速度y的比值，即:

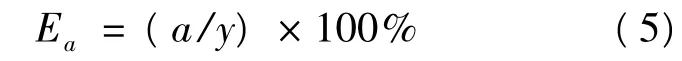
以上各式中y，k，l都可以从历史资料分析中得到［8-9］，因此用适当的方法估计出α，β后就可以计算出广义的技术进步的年平均增长速度a。

2.2 科技进步贡献率测算模型的设计

用余值法模型计算科技进步贡献率，在时间上宜作5年以上的分析，并且适合国家及地方计算科技进步贡献率，否则容易导致信息失真，因为科技进步贡献率的动态曲线反映的最主要信息是科技进步的长期发展趋势和对一般规律的概括和描述［10］。考虑到油田历年从事油气生产业务，生产经营相对稳定，产量(考虑产量递减因素)、投入基本稳定，劳动力也无太大波动，同时科技进步对经济增长贡献具有累积性、长期性和滞后性，不会出现政策变化、市场波动、人们的心理预期大起大落的变动;在技术处理上，α，β系数采用10年以上数据统计回归和DEA技术修正。因此，所建立的油田企业科技进步贡献率测算模型能较好反映上述生产要素的长期贡献趋势，结果具有可信度。

2.2.1 相关指标的选取及计算

(1)产出Y。选择原油产量作为产出指标Y，与工业总产值、收入和利润等指标相比，产量能够避免油价上涨等因素的影响，起到不变价格的作用。由于油田勘探开发具有资源有限性，产量呈阶段递减特点，因此，必须借鉴等效益面法，考虑反映产量递减的系数η1，笔者的研究采用自然递减率对油田的产出(产量)进行调整，调整后的公式为:

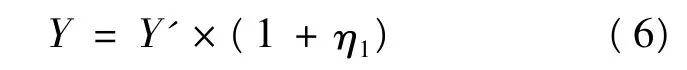
式中:Y'为年实际的产油量;Y为理想产油量;η1为产量递减系数(在实际计算中选用油田的自然递减率)。

同时，产出年增长率为:

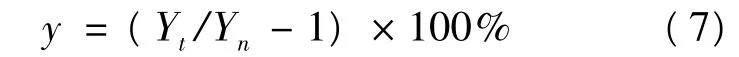
式中，Yt、Yn为计算期、基期的产出量(修正后的理想产量)。

石油生产的特殊性决定了其科技进步增长速度的计算与一般加工业不同，如有较强的资源制约性，原油产量存在自然递减规律，因此需要通过自然递减将实际产量调整为理想产油量，使计算结果更加符合油田实际。

(2)资本投入K。在实际的测算中，采用固定资产的原值。固定资产原值在一定程度上能够消除价格变动的影响。设油田企业资金投入量的增长速度为k，则:

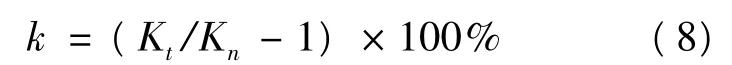
式中，Kt、Kn分别为计算期和基期的资金投入量(固定资产原值)。

(3)劳动力投入L。按照生产函数的本意，劳动投入L是指劳动的实际投入量。从实证计算来看，对劳动投入量的计算主要有两种方法:一是计算劳动力的数量(职工人数)，二是计算劳动者报酬(工资总额)。由于采用劳动者报酬作为劳动力投入，存在工资变动等不可比因素，故用劳动力数量来表示劳动投入量，在测算中采用了油田各年年末的在册职工人数。同样，可知油田企业劳动力投入量的增长速度l的计算公式为:

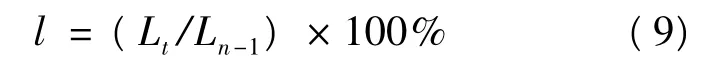
式中，Lt、Ln-1分别为计算期和基期的劳动力投入量(年末职工在册人数)。

2.2.2 资本与劳动产出弹性系数的确定

在具体实践中，资本、劳动力同时发生变化，而且变化幅度不同，因而α、β难以确定和验证。确定弹性系数α、β一般采用经验值和统计回归计算取得。经验值获取简便，但数值可能与实际背离较大，而运用统计回归计算取得α、β，更能符合油田实际。因而采用生产前沿面函数的办法。用费莱尔测度方法确定企业有效生产前沿面，及不同年份在它上面的投影。DEA模型选取用于评价技术效率的基于输出的具有非阿基米德无穷小的C2GS2模型。

设Xj为第j年的投入量，Yj为第j年的理想输出，j=1，2，…，n。则可得模型为:

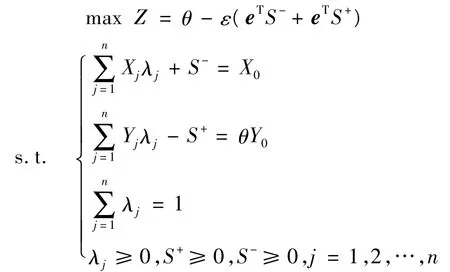
式中:ε为无穷小的正数，在实际的测算中取值为10-6;Z为产出效率评价指数;e为权系数矩阵;θ为系统总产出;λ为投入量(因素)权系数;S为资本、劳动力等资源投入量，S+为过度投入，S-为产出的不足。

假设模型求得的变量最优解为:

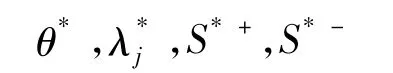
(1)技术有效及无效的年份修正。若模型的最优解 θ*=1，则说明被评价决策单元 j0是C2GS2下的弱DEA有效。

若θ*=1，S*+=S*-=0，则说明被评价决策单元j0是C2GS2下的DEA有效。

此时，意味着Y0和Xj有效，可直接计算。

若θ*＞1，说明被评价决策单元j0是C2GS2下的非DEA有效，S*+表示过度投入，S*-表示产出的不足。这时需要通过求得无效的评价年份在有效生产前沿面上的投影来修正。此时:

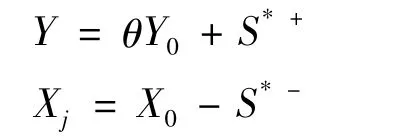
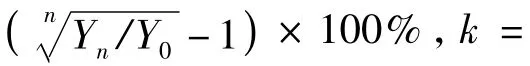
3 计算中可能存在的问题及分析

(1)关于α+β＜1的问题。如果在测算中资本产出弹性系数与劳动产出弹性系数之和α+β＜1，则说明油田生产的总体情况是生产规模收益递减。这也许符合油田实际，如油田的原油特点是埋藏深，地质条件差，稠度高。在生产能力达到一定的水平后，增产难度很大，因此在这种情况下，生产规模的扩大反而会带来效益的下降。因此α+β＜1往往由被测算油田本身的特点来决定。

(2)关于α＜0的问题。如果在测算中通过数据分析得出α＜0，看似不合理，但借鉴经济学中的效用理论，劳动力产出弹性系数为负是可以解释的，其根本原因是劳动力的冗余。因此α＜0如实地反映了油田生产过程中存在的人力资源配置与使用缺乏科学性和合理性。

(3)关于β值很大的问题。该问题的出现与油田企业的资金密集型生产的特点分不开，如某油田的平均资金装备率为17.7万元/人，而同期全国企业平均资金装备率不足1万元/人 ，资金装备率的高低在一定程度上影响了资金产出弹性系数的大小。β值高也从另一个方面说明了被测算油田产出的增长对固定资产投资的依赖性。

4 结论

笔者提出了油田企业科技进步贡献率的基本内涵、影响要素与测算准则，以索洛余值法为基础设计了油田企业科技进步贡献率的测算模型，并给出了部分变量的调整计算方法，指出了实际测算中可能出现的问题并分析其原因。利用该测算模型建立的评价体系对2004年胜利油田获奖的科技成果进行模拟评价和分析，该体系将科技成果分为8个专业(石油地质、地球物理勘探、钻井工程、测井工程、录井工程、油藏工程、采油工程和地面工程);并按成果的经济效益表现形式，分为4种类型(新增储量类、增加产量类、技术服务类和产品类)。不同类型成果经济效益的计算分别采用与其特点相一致的模型，并基于该方法设计了配套的软件，运行得到的评价结果与原来获奖排序符合度在70%以上。

［1］王桂荣，王慧军.河北省农业科技进步贡献率测定结果与分析［J］.河北农业大学学报，2003(5):306-309.

［2］陈思蓉.基于柯布-道格拉斯生产函数对我国经济增长的实证检验［J］.金融经济，2007(10):83-84.

［3］傅诚德.科学技术对石油工业的作用及发展对策［M］.北京:石油工业出版社，1999:31-98.

［4］魏和清.科技进步贡献率测算中资本投入度量问题研究［J］.当代经济，2004(8):122-126.

［5］罗伯特·M·索洛.经济增长因素分析［M］.史清琦，译.北京:商务印书馆，1991:76-103.

［6］DENIS C，MCMORROW K，ROGER W.An analysis of EU and US productivity developments［R］.［S.l.］:European Communities，2004.

［7］HULTEN C R，DEAN E R，HARPER M J.Studies in income and wealth［M］.Chicago:University of Chicago Press，2001:86-123.

［8］王天营.我国经济增长中科技进步贡献率的计量分析［J］.生产力研究，2003(5):49-52.

［9］丁浩，叶志刚.胜华炼油厂科技进步贡献率计算与分析［J］.经济师，2003(9):264-265.

［10］孙建召，曾巧明.索洛余值法模型研究及其应用［J］.计算机技术与发展，2006(9):139-141.