博弈论在建设工程分包管理中的应用

◎

引言

一直以来，工程项目的建设过程中的分包管理一直是很多施工企业头痛的问题。在工程项目管理中，由于竞争压力，总承包面临着成本控制的现状，总承包必须严格筛选分包单位，挑选出价廉但是质量过关的分包单位作为长期合作伙伴。

在施工企业中是存在很多博弈的，有些是静态博弈，有些是动态博弈；有信息完全下的博弈，也有信息不完全下的博弈。其中，项目的分包管理就可以用完全信息静态博弈和完全且完美信息动态博弈来分析。

1 总承包商与分包商之间的博弈模型

1.1 博弈模型的建立

1.1.1 基本假设

假设1：参与人。工程项目的分包管理的博弈模型中，为了讨论方便，只假定2个人，即总承包商（参与人A）和分包商（参与人B）。

假设2：参与人A和参与人B都是理性且为他们各自最大的利益考虑。

假设3：博弈双方采取的行为。用SIJ表示参与人在博弈中的特定行动。S1=（S11，S12）表示总承包商的纯战略空间，其中S11表示总承包商压价的行动，S12表示总承包方不压价的行动；S2=（S21，S22）表示分包商的纯战略空间，其中S21表示分包商续约合作的行动，S22表示分包商不续约的行为。这样就得到了四种组合即为（S11，S21）、（S11，S22）、（S12，S21）、（S12，S22）。假设每个参与人都独立采取自己的策略，或行动时间有先后顺序与同时行动的结果是相通的，并且只进行一次，即认为这是一个静态博弈。

假设4：信息。假设参与方都对其他人了如指掌，基于第三、四个假设，所涉及到的博弈模型为一个完全信息静态博弈模型。

假设5：期望收益。假设参与人A，压价后利润为a，原利润为b，（由上述文字也可以知道a> b> 0），参与人B，原先利润为c。参与人A压低价格，与参与人B去协商，付出的成本是e（假设a-b>e），协商成功时，参与人B损失的利润为d=a-b>0。

1.2 基于完全信息静态时的博弈

假设该博弈模型是完全信息静态时的博弈，即参与人A和B都知道对方信息，同时进行的博弈。则根据上述假设得出相关矩阵图如图1：

图1

图2

图3

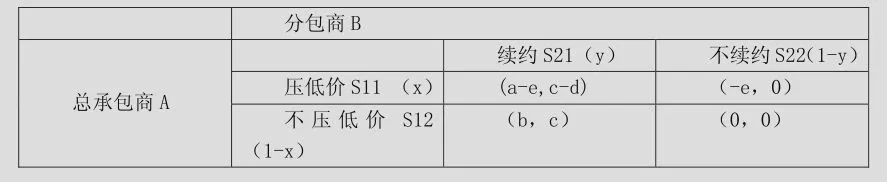
图4

1.2.1 纯战略纳什均衡

根据图1，讨论各种情况下的纳什均衡

因为给定假设a-e>b，则有2种情况：c-d>0或者c-d<0需要讨论，下面就针对这2种情况讨论。

（1） c-d>0，如图2。

根据划线法得，纯战略纳什均衡为(a-e,c-d)即总承包商选择压低价格，分包商选择续约。

（2）c-d<0，根据划线法可以得图3。

根据划线法，不存在纯战略纳什均衡。

1.2.2.混合战略纳什均衡

在c-d<0 ，图3中不存在纯战略纳什均衡，因此需要建立混合战略，并求其混合战略的纳什均衡。假设x为总承包商压低价格的概率，y为分包商续约的概率，可以得到混合战略博弈模型支付矩阵如图4。

通过支付矩阵求混合纳什均衡解释如下：

对于给定的x，分包商选择续约（y=1）和不续约（y=0）的期望值分别为：

ΠB(x，1)=x*（c-d）+c（1-x）=c-dx

ΠB（x，0）=0

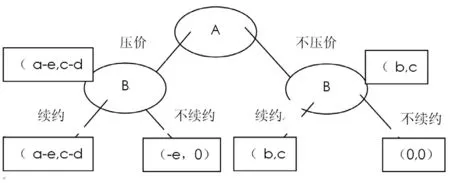
令ΠB(x，1)= ΠB（x，0），则x=c/d (c

对于给定的y，总承包商选择压价（x=1）和不压价（x=0）的期望值分别为：

ΠA(1，y)=y*（a-e）+（-e）（1-y）=ay-e

ΠA（0，y）=by

令ΠA(1，y)= ΠA（0，y），则y=e/（a-b）

即可得到混合纳什均衡点（x= c/d，y= e/（a-b），即总承包商压低价格的概率为c/d，分包商续约的概率为e/（a-b）。

1.3 基于完全信息动态时的博弈

以上讨论了完全信息静态博弈的情况，但在实际分包工作开展工作中，往往都会讨价还价后，选择继续合作或者不合作。这就转变成了完全且完美信息动态博弈。每个参与人是先后根据对方的选择而进行下一步计划。

1.3.1 完全且完美动态型基本假设

假设1：承包商是参与人A，分包商为参与人B。

假设2：承包商A和分包商B都是理性人，都是以自身利益最大化为最终目标。

假设3：在博弈过程中，后行动者都能了解之前所有过程，对他来说，他是完美信息。

假设4：期望收益。假设参与人A，压价后利润为a，原利润为b，（由上述文字也可以知道a> b> 0），参与人B，原先利润为c。参与人A压低价格，和参与人B去协商，付出的成本是e（a>e），协商成功时，参与人B损失的利润为d=a-b>0。

1.3.2 建立完全且完美信息动态模型

在这里采用博弈树来分析，如图5。

1.3.3 子博弈完美纳什均衡

在上面图7中可以看出有2个子博弈模型，这种博弈树都采用逆向归纳法。可以得出2种结论：

当c>d时，分包商B选择续约，所以必须要讨论a-e和b的关系；

当a-e>b时，总承包商A会选择压低价格；

当a-e

当c

在这里只有1个子博弈完美纳什均衡（b，c）。

图5

2 纳什均衡对承包商与分包商关系确立的指导意义

2.1 完全信息静态博弈

当c>d时，纯战略纳什均衡为(a-e,c-d)，总承包商选择压低价格，分包商选择续约，双方都是有利润的。

当c

2.2 完全且完美信息动态博弈

当c>d时，表示分包商B想续约的，因此就必须讨论a-e和b之间的关系。

如果a-e>b时，即总承包商A即使花钱和分包商协商了，但是最后总承包商的利润还是比原来多，那么总承包商A选择压价。

如果a-e

当c

3 结语

本文运用了博弈论中的完全信息静态博弈对施工管理中的承包商与分包商之间的博弈分别在完全静态博弈和完全且完美信息动态博弈下建立模型进行了分析，并计算他们的混合纳什均衡及子博弈纳什均衡。最后分析了对承包商和分包商之间的选择给出了最优决策的指导。

当然，在实际的过程中，问题要比本文现在分析的单一状态还要复杂，必定会出现多方博弈，然后由总承包商按照利润最大、效益最高进行优先选择合适的分包商进行合作，因此，本文只能作为现实操作中的借鉴。