多梁钢桥由梁间相对位移及扭曲引起的疲劳应力估算浅析

◎

引言

通常钢梁横向加劲肋与腹板的焊缝连接至靠近钢梁受拉翼缘处，受拉翼缘与腹板之间留有5～10cm左右的间隙。此处将这部分未加强的腹板称作腹板间隙。1985年以前，施工中也经常不将加劲肋与钢梁受拉翼缘连接在一起（图1）。这种施工方式使得当横向加劲肋作为梁间横隔的连接板，并且由同一横隔连接的钢梁产生不同的竖向位移时会引起疲劳问题（图2）。由于梁间的相对位移，横隔产生转动，使得腹板产生平面外扭曲。腹板间隙区域利用其自身弹性来适应大部分扭曲。由于钢梁上翼缘受到上部混凝土板面的约束，负弯矩区的腹板间隙尤其容易受到扭曲疲劳问题的影响。

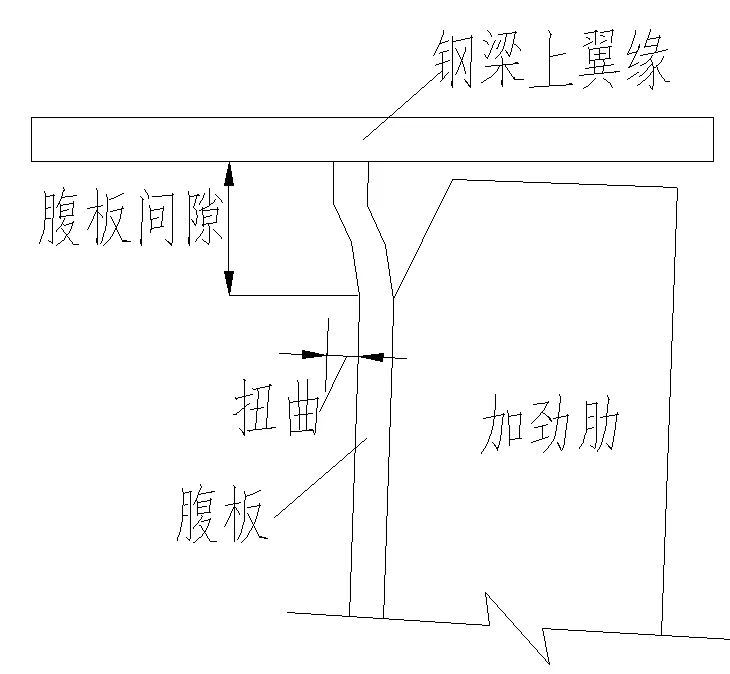
图1 腹板间隙示意图

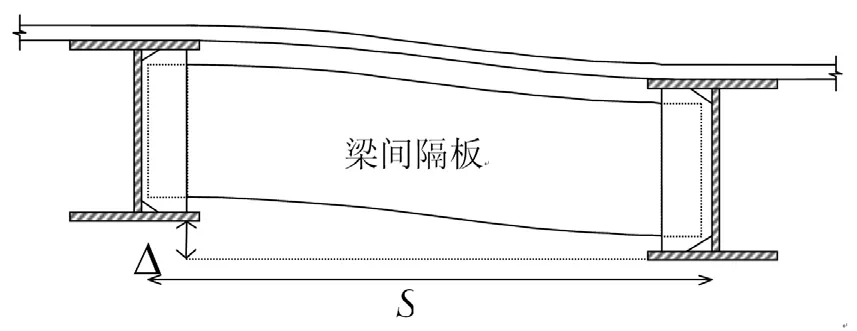
图2 梁间横隔板及变形示意图

1 桥梁有限元模型建立

采用有限元软件 SAP2000 对明尼苏达州的I94/I694桥（I94/I694 Bridge）及普利茅斯街大桥（Plymouth Ave.Bridge）建立整体模型及细部模型进行分析。其中I94/I694桥采用的是弯板隔板，普利茅斯街大桥采用的是交叉支撑横隔。

2辆总重量222kN的卡车被用来模拟桥梁上的荷载情况，包括卡车并行通过，单独靠右侧或左侧通过等各种不同的工况。将卡车荷载按照上述工况分别施加在桥梁整体模型上的不同位置进行计算，从中找出每座桥上钢梁间隔板的最大竖向相对位移 ，及对应此变形的节点。再将发生最大相对位移的隔板及两侧钢梁截取出来建立细化的有限元模型（细部）进行分析，将整体模型计算得到的竖向位移及节点绕桥面纵向边线的转角加到细部模型中钢梁上翼缘的各节点上进行计算。计算结果显示，腹板间隙在上述荷载作用下产生上部、下部旋转变形及少量的平面外偏转。

在文献[4]和[5]中，腹板间隙部分被假定为两端固定，各项同性的梁。线弹性理论可以用来建立该梁端矩，转角及侧向变形的关系，根据端矩及腹板间隙的几何参数，腹板间隙应力计算公式如下：

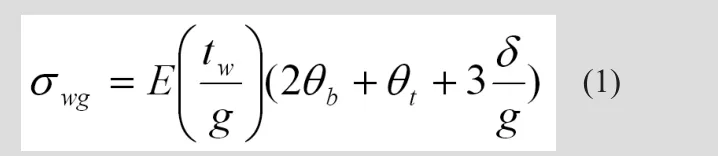
2 钢梁间相对位移的估测

为了确定与预测钢梁间相对位移Δ相关的参数, 对明尼苏达州的桥梁进行了一系列分析。文献[2]定义了与明州桥梁系列相符的建模及设计标准。

2.1 钝角效应

在有限元模型形成前，首先对行车道荷载的影响进行了研究。选取一个与I94/I694桥类似的斜桥端跨，通过对1辆最大轴距9.1m的HS-20型卡车分别行驶在每个车道内（共4个车道）的分析表明，对于仅一个行车道加载的情况来说，最大的梁间相对位移发生在该车道的钝角位置（图3）。

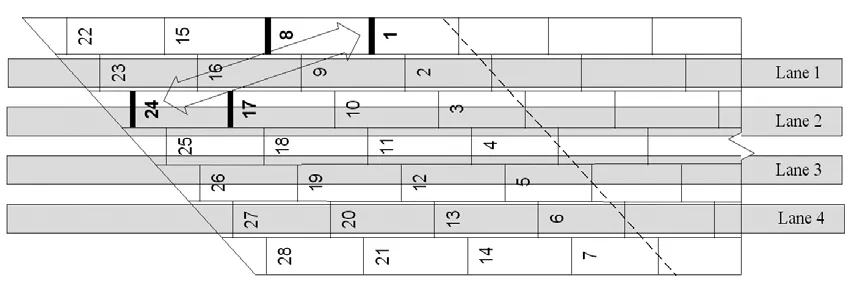
图3 车道1加载钝角效应

图4 桥梁整体模型中横隔编号示意图

2.2 弯板隔板的相对位移

文献[2]研究表明以下公式可以用来准确的模拟弯板隔板桥梁模型的最大梁间相对位移：

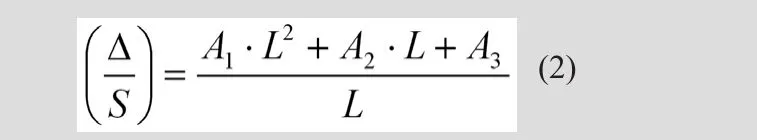
其中，Δ为梁间最大相对竖向位移，S为相邻钢梁横向间距。公式（2）是桥梁跨度L的函数，其中常数项A1、A2及A3的数值如表1所示（对应斜角20°、40°及60°）。对于不同于20°、40°及60°的斜角，可以通过内插法来确定A1、A2及A3的数值。此外，对与HS-20卡车有相同轴距，但重量不同的卡车荷载或不同的桥面厚度应考虑到适当的修正因子。

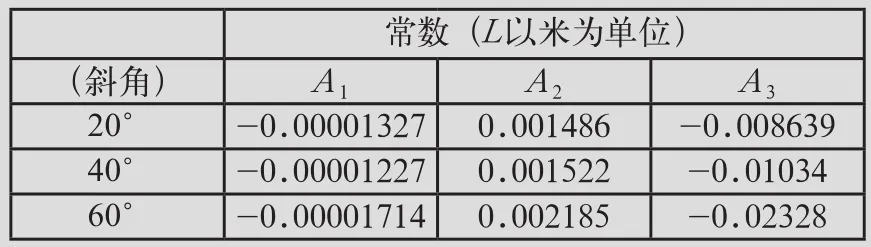
表1 公式（2）中的常数取值

2.3 对222-kN卡车荷载的修正因子

现场试验中使用的明州交通部自动倾斜运砂车为222-kN的卡车，与AASHTO美国国家公路与运输协会的标准HS型号卡车轮轴不同。为了确定卡车荷载构造差异的影响，对桥梁模型中钝角位置的隔板（图4中的隔板A、H及O）进行了分析。钢梁间距3.20m，分别将HS-20及222-kN卡车荷载加在上述隔板上，对最大竖向相对位移进行比较。在两种卡车荷载作用下的最大相对位移值的比值的最佳适配曲线可以用下式来表示：

定义比例因子 RL=Δ222-kN/ΔHS-20，其中Δ222-kN为222-kN 卡车荷载作用下的最大相对位移，ΔHS-20为HS-20卡车荷载下的最大相对位移。由于上述公式推导时使用的长度单位为英尺，跨度L的单位应转换为英尺(ft)后代入计算。

2.4 交叉支撑横隔的修正因子

文献[8]研究的结果表明与弯板隔板相比，交叉支撑横隔可以减小钢梁相对竖向位移。将HS-20卡车荷载施加在外侧车道上，对梁间距分别为2.44m、2.82m及3.20 m 的模型分别用两种横隔类型（弯板隔板及交叉支撑横隔）进行测试，找出最大横隔竖向位移。 比例修正因子Rx=Δcb/Δbp定义为由于交叉支撑横隔刚度加强引起的公式（2）中最大相对位移折减系数。其中，Δcb 代表交叉支撑隔板桥梁的最大梁间相对位移，Δbp 为弯板隔板桥梁的最大梁间相对位移。研究表明，对于不同的钢梁间距模型，Rx近似为跨度L的函数，与桥梁斜角（即与河岸的夹角）关系不大。该趋势由多项式公式（4）来模拟，对不同的钢梁间距，常数B1与B2取值不同。 常数 B1、B2 的取值列于表2。对钢梁间距2.82 m与3.20 m之间的采用内插法确定。

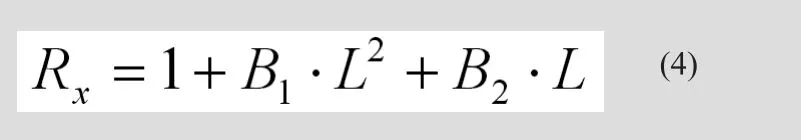
表2 公式（3）中的常数取值

3 腹板间隙扭曲应力估算

3.1 隔板参数研究

公式（1）用来计算腹板间隙应力。其中θb、θt及的数值没有现场监测数据时难以确定 。应进行参数研究来确定隔板几何参数对腹板间隙扭曲问题的影响。分别改变g、tw、桥面厚度td、梁上翼缘厚度tf及相对位移，并查看模型的结果。腹板间隙转角θb、θt及侧向偏转被/S归一，以找到腹板间隙应力与梁间相对位移的简单关联。I94/I694桥和普利茅斯街大桥研究的各变量及相应的归一数值列于表3、表4，表中对该两座桥的原始模型数据也进行了标注。

表3及表4表明所有研究的参数对腹板间隙应力都有影响。对所有参数来说，数值（2θb+θt）/（Δ/S）比θb/（Δ/S）和θt/（Δ/S）一致得多，然而（δ/g）/（Δ/S）并没有明显的趋势。定义C=（2θb+θt）/（Δ/S），平均后，对I94/I694桥取C=2.25，对普利茅斯街大桥取C=2.75。用常数C加上分析中记录到的侧向偏转δ及相对位移Δ，腹板间隙应力就可以由公式（1）来估测。在文献[8]对I94/I694桥及普利茅斯街大桥的现场监测中，没有发现腹板间隙区域有明显的的侧向偏转δ。因此，在缺乏一种简单的方法来预测δ并对该偏转在实际桥梁中是否存在持保留意见的情况下，暂可在应力预测公式中忽略掉的影响。这样，确定了常数C=（2θb+θt）/（Δ/S）后，腹板间隙最大应力预测公式可简化为：

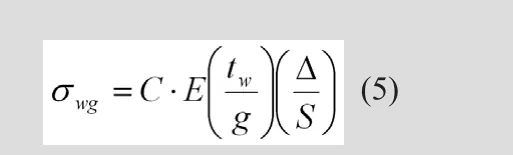
3.2 I94/I694 桥梁原型变量的参数研究

桥梁整体模型用来研究跨度L、斜角βs及钢梁间距S对腹板间隙应力预测的影响。细部模型截取整体模型中的一个横隔进行分析，边界条件及荷载数据均由整体模型结果来确定。由此进行双重模型分析。已知最大相对位移发生在主跨的钝角区域，因此重点研究1辆222-kN卡车在车道1加载情况下的横隔A、H及O（图4）。分别计算钢梁间距3.20 m、斜角20°、40°及60° 情况下的桥梁弯板隔板A、H及O的数值C=（2θb+θt）/（Δ/S）。结果表明，桥梁主跨C的数值对于靠近桥墩和远离桥墩的横隔板是不同的。 随着桥梁斜角的变化，C的数值变化不大。跨度L与横隔板相对于桥墩的位置是影响系数C数值的两个主要参数。公式（6）给出了对于钢梁间距3.20m的桥梁系数C较为准确的估测。以下公式中跨度 L的单位仍为英尺（ft）。

此外，对钢梁间距2.44 m和2.82 m，斜角s=60°的模型也进行了计算。总体上，与跨度的影响相比钢梁间距对系数C值 的影响是非常小的。

3.3 普利茅斯大街桥梁原型变量的参数研究

如前所述，普利茅斯街大桥采用的是交叉支撑横隔。同样进行双重模型分析。与弯板隔板下的结果类似，斜角变化及钢梁间距变化对交叉支撑隔板的C值影响很小。公式（6）预测弯板隔板和交叉支撑横隔均能得到满意的结果，此处无需校正。

3.4 最大腹板间隙应力

计算表明，大多数情况下公式（2）～（6）结合，能够给出最大腹板间隙应力σwg的合理估测。在个别情况下，可能会有较大误差，原因在于根据有限元分析结果，腹板的侧向偏转量δ有时较大。为了得到更为合理的腹板间隙应力预测数值，δ也应当与Δ/S及C一起考虑在应力计算公式中。虽然最大相对位移发生的隔板不一定会产生最大腹板间隙应力，但是如果将δ包含进来后，前面提到的应力预测方法仍是令人满意的。目前为止，还没有确定有效的预测腹板侧向偏转δ的方法，仍然需要更多的现场试验来找出扭曲疲劳问题中腹板侧向偏转量δ的特点。因此，建议上述提到的方法用于明尼苏达州交通部桥梁系列中有交错排列横隔的多梁钢桥，如果有证据表明腹板间隙侧向偏转量不可忽略时应当考虑到该值的影响。

结束语

本研究表明，腹板间隙同时产生上部、下部旋转及少量平面外偏转，因此腹板间隙应力预测公式应同时考虑到这些变量。

(1)桥梁建模后，计算出了最大梁间相对位移Δ，并提出了弯板隔板桥梁预测相对位移与钢梁间距比Δ/S 的多项式。 同时，对于不同卡车加载形式及交叉支撑横隔的影响进行了修正，给出了修正因子的计算公式。

(2)研究发现，腹板间隙应力公式中的(2θb+θt) 除以Δ/S后的数值对各横隔基本一致，因此将该比值定义为一个常系数C。对于靠近桥墩与远离桥墩的隔板，C分别为桥梁跨度L的线性函数，钢梁间距与桥梁斜角对C值影响不大。

如果有证据表明腹板侧向偏转量可以忽略，腹板间隙应力可以由本文提出的远离桥墩隔板的系数C，结合Δ/S计算的公式来进行预测。要考虑到腹板间隙侧向偏转的影响，需要进一步的研究及现场试验，以得到更为准确的最大腹板间隙应力预测结果。