基于最大熵的坝体健康评估专家模糊赋权模型
2011-09-05方春晖李占超
杨 阳,方春晖,李占超,秦 栋
基于最大熵的坝体健康评估专家模糊赋权模型
杨 阳1,2,方春晖2,李占超1,2,秦 栋1,2
(1.河海大学水文水资源与水利工程科学国家重点实验室,南京 210098;2.河海大学水资源高效利用与工程安全国家工程研究中心,南京 210098)
针对坝体结构在运行期受外在环境影响因素复杂,定性和定量因素相关程度高,并且含有大量缺失和模糊不确定性的特点,利用模糊数学理论构建坝体健康评估的专家模糊赋权系数。在此基础上用GA算法依据最大信息熵原理对模糊权系数进行优化,综合坝体各个方面的多种评估,形成多层次的坝体综合模糊赋权模型。选用新安江重力坝作为评估实例,对变形、渗流、应力应变等多个方面进行评估,并形成综合评估结果。实例获得了较好的分析评估结果,对所提出的方法进行了验证。
坝体;健康;赋权;最大熵;模糊数学
1 概 述
大坝作为一个构建在河床上的挡水结构,在施工、蓄水及之后长期的水库调节运行过程中不断地受到外在环境的影响,其影响因素包括水压、温度、降雨、地下渗流等。这些复杂多变的因素对坝体结构经年累月的作用足以对坝体的运行状况和后期健康状况产生极大的影响。坝体健康评估是了解坝体实际运行状态及健康状况的有效方法。
坝体健康评估时,视大坝为一个复杂的动态系统,运用一定的力学知识和系统科学的方法,研究坝体接受环境的影响输入和大坝监测信息的响应信号输出之间的关系,从而分析得到坝体的内在运行状态和健康程度。在实际的评估过程中,影响因素[1]往往种类繁多、相互关联。这就需要具有知识和经验的专家人才,运用综合、分析、归纳等逻辑思维,通过因果推理、反思,最终找到由因到果的关联,进而由果到因反向思维,提出基本的决策措施。这个思维过程中要考虑的因素繁多,既有定量化的指标,也有定性的信息。由于外在环境的多变和监测信息的繁杂,其存在大量的模糊性和随时间变化的不确定性,并有局部缺失。因而,专家对信息主次轻重的分离、删选就显得尤为重要,如何正确有效地收集专家对信息权重的主观评定,并合理地综合集成多个专家的观点,最终形成对信息正确有效的权重划分,就成为一个关键性的问题。基于此,本文提出模糊赋权模型,先基于专家思维的模糊性和参照不确定性,形成专家模糊评判矩阵得到模糊权系数。进而考虑到单个专家思考的局限和片面性,选取多个专家进行取值,进行最大信息熵的优化。最后结合多层次的坝体整体健康评估框架,形成坝体健康综合评估专家模糊赋权模型。
2 模糊评判矩阵及其权系数
人对信息的描述往往是模糊不确定的,总是需要参照一个基本的标准才能对信息做出相对的描述。因而,专家要对影响大坝的多个因素进行主次轻重的分离、删选就需要有所参照,基于此,利用模糊数学的原理,通过专家建立模糊评判矩阵进而得到权系数。
2.1 模糊评判矩阵[2]
设坝体健康评估的指标集V=[v1,v2,…,vi,…,vn](式中vi为本层中第i个指标,本层共有n个指标),对应指标集的模糊评判矩阵[R]为
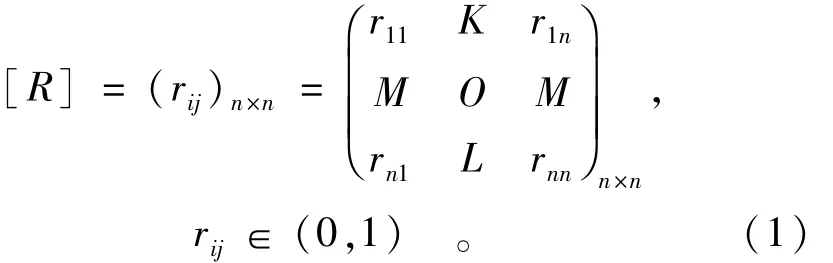
式中rij表示评估指标vi比vj重要程度的比值,vi比vj越重要,则rij越大。一般来说当rij>0.5时,vi比vj重要。1-rij表示vi比vj不重要的程度,即是说vj比vi重要的程度,因而1-rij=rji。
对应指标集的模糊权系数为

式中wi是对应指标集中vi的权重系数,其表示本层指标vi对上一层综合指标的重要程度。由此可知,wi是对vi的重要性的度量,wi越大则vi就越重要,所以,wi-wj的值则反映了vi比vj的重要程度,这与rij的定义是相关的。因而可以建立wi,wj和rij这三者之间的关系,即rij=f(wi-wj)。
2.2 模糊权系数确定
通过专家对本层评估指标v1,v2,…,vi,…,vn进行两两之间的评估对比取值,可得到模糊评判矩阵[R]=(rij)n×n,由前述公式rij=f(wi-wj),及文献[2]得到wi,wj和rij这三者之间的关系为
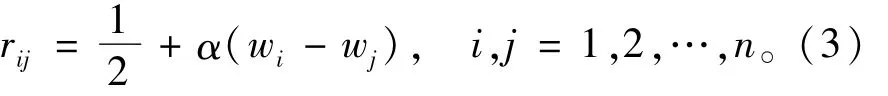
式中α表示专家对指标之间重要程度差异的重视程度,可在区间(0,0.5)内取值,当α取值较大时,评估结果中指标vi相对于指标vj就更加重要,最终结果中指标vi占的比重就大,反之亦然;当α在公式中取值不变时,因为权系数要满足归一化条件,α则不产生影响。
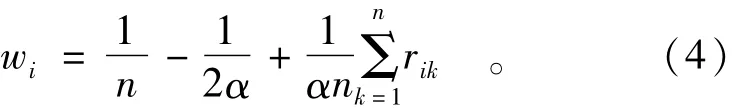
依照模糊矩阵的建立方法和对权系数的计算过程,建立以下计算流程,选取m位专家依此计算每位专家的评判权系数,形成m位专家的权系数矩阵W,每一列表示m位专家对同一指标的不同权重取值,每一行表示同一个专家对本层所有n个指标的权重取值。
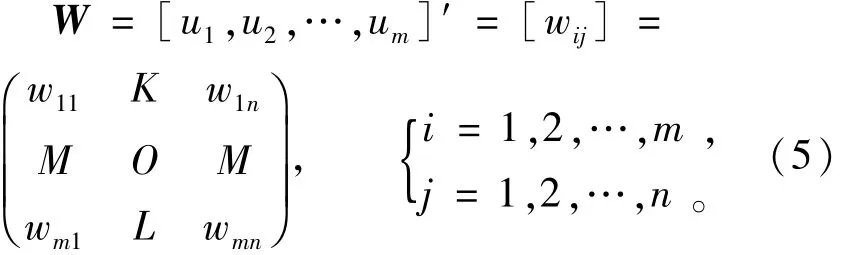
3 最大熵原理的权系数优化
专家的知识结构、自身素质、思维方式等各不相同,因而对同一问题的侧重点也不同,对同一指标重要性的估量也不同。加之影响因素众多,专家人数有限,m位专家的权系数矩阵很难全面有效地覆盖所有相关因素。以下基于最大信息熵原理[3-5]对专家权系数矩阵进行优化,达到最优的指标权重[6],最优化方法选取遗传算法。
3.1 权系数的最大熵
前述得到的m位专家的权系数,可视为在权系数样本空间中选取了m个值,即获得了m位专家对指标权重的评定信息,这些评定信息很难包括对指标重要性的所有描述,但由于专家数量有限,获得大量专家评定结果却又是不可能的。依据最大信息熵原理,在所有权重的可行解中,选择信息熵取得极大的解为最优值,这样的结果更加接近于实际情况。对于离散的专家权系数,相对某个指标,可得到权重信息熵的公式为

式中:H(w)为权重信息熵;wi为同一指标的不同专家权系数;qi表示对某个指标权系数重要程度,其在一定程度上反映了某位专家的重要性。当取得max(H(w))时,可求得对应的w为最大熵条件下的权重值
3.2 遗传算法的最大熵优化
遗传算法GA(genetic algorithm)模仿大自然的物竞天择和生物自身个体的基因遗传机制,通过特定环境的不断选择和生物体内基因对环境的适应遗传,经过数代的杂交、变异,最终得到最适合环境的生物基因,即最优解。遗传算法是求解复杂系统问题的通用算法,具有并行性和鲁棒性。基于此搜索方法,为求得最大信息熵,建立以下目标函数:
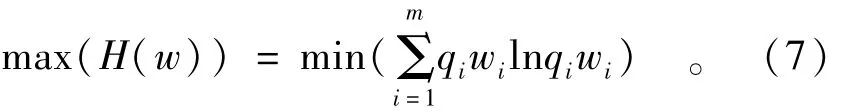
随机选取qi∈(0,1),i=1,2,…,m,作为初始种群,并有约束条件可计算得到m位专家对n个指标的权系数重要度矩阵,其描述了每位专家对每个指标评定结果的重要性。结合权系数矩阵和重要度矩阵,最终得到最优化的综合指标权重为

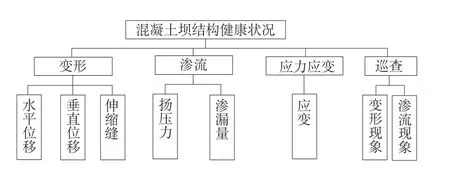
图1 健康评估体系Fig.1 System of dam health assessm ent

图2 计算流程Fig.2 Flow chart of calculation process
4 多层次坝体综合模糊赋权模型[7]
对影响坝体健康的相关指标进行分类,按照层次划分,形成基本的健康评估指标框架(图1),将最大信息熵化的综合权重融入指标框架中,最终形成多层次的综合模糊赋权模型,具体计算流程如图2。
5 实例分析
选取新安江大坝为分析实例,依照健康评估框架划分为3个层次,选取中间层指标:变形、渗流、应力应变及巡查为基本指标,邀请3位相关专家,建立综合专家模糊赋权模型。
5.1 模糊评判矩阵的建立和权系数求解
经过3位专家甲、乙、丙对新安江大坝的全面了解,对变形、渗流、应力应变及巡查指标给出两两对比的模糊评判矩阵,如下:

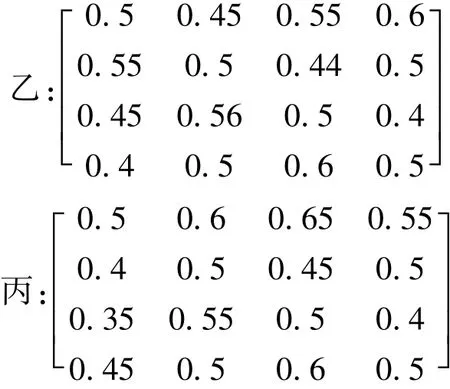
按照式(4)可求解每位专家对4种指标的权系数,如表1。
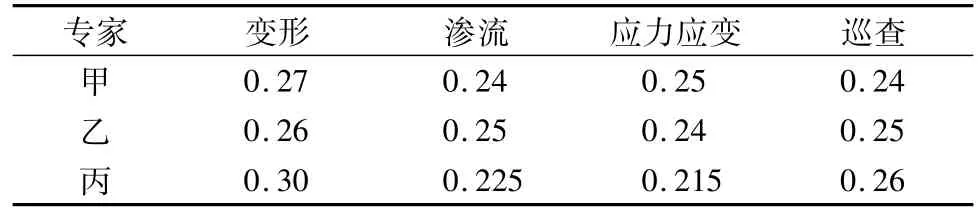
表1 专家权系数Table 1 Data of experts’weight coefficient
5.2 最大信息熵的优化和综合权重求解
编写Matlab语言的GA遗传算法程序,计算3位专家对同一指标的权系数重要程度qij(i=1,2,3,j=1,2,3,4),形成权系数重要度矩阵Q,如表2。
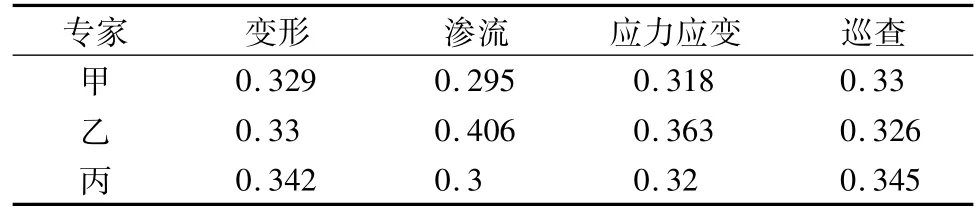
表2 权系数重要度Table 2 Im portance degree of weight coefficient
用公式(8)计算指标综合权重,可得到Ws=Q′W=[0.283 0.238 0.237 0.253]。
6 结 论
结合新安江大坝实际情况,通过对指标综合权重的分析,得到以下几点结论:
(1)变形监测体现的是整个坝体结构的位移变化,是对坝体最直观的信息。水位、温度等对大坝的影响能较明确地反映在坝体变形上。因而坝体变形相对于其它更能体现出坝体的运行状态和健康程度,因而得到了较大的专家综合权重。
(2)巡查形象直观可靠,文字图片包含信息量大,最切实地反应了坝体结构部位的变化情况。并且,人脑对图片文字等感知、记忆力强,相对于其它数据、图表信息,专家对巡查信息有更多的感受,所以得到了相对较大的权重。
(3)渗流主要反映坝体、坝基及两岸地下结构状况,受降雨、温度的影响较大,权值较小。应力应变仪器损坏较多,有效测点较少、测点方差较大、精度较低,难以反映内部真实并且在2005年之后完全停测,因而获得的权重最小。
通过以上分析可看出,基于人类思维的模糊不确定性和思考的局限性、片面性,选取模糊评判矩阵得到专家权重系数,进而通过信息熵的最大化得到较优的专家权重,结合坝体健康评估框架形成了坝体健康评估专家模糊赋权模型。实例结果充分提取到了专家知识思考的成果,又避免了专家思维模糊性和片面性,权重结果和大坝的实际情况有较好的印证,此方法也可以很好地拓展到其它需要对专家知识提取和优化的应用中。
[1] 蔚维斌,李珍照.混凝土坝安全综合评价指标体系探讨[J].大坝与安全,1995,33(3):31-34.(WEIWei-bin,LI Zhen-zhao.Investigation of Dam Safety Evalua-tion Index System[J].Large Dam and Safety,1995,33(3):31-34.(in Chinese))
[2] 吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,(2):79-85.(LU Yue-jin.Weight Calculation Method of Fuzzy Analytical Hier-archy Process[J].Fuzzy Systems and Mathematics,2002,(2):79-85.(in Chinese))
[3] 周惠成,张改红,王国利.基于熵权的水库防洪调度多目标决策方法及应用[J].水利学报,2007,38(1):100-106.(ZHOU Hui-cheng,ZHANG Gai-hong,WANG Guo-li.Multi-objective Decision Making Ap-proach Based on Entropy Weights for Reservoir Flood Control Operation[J].Journal of Hydraulic Engineering, 2007,38(1):100-106.(in Chinese))
[4] 陈 斌,刘 宁,卓家寿.岩土工程反分析的最大熵原理[J].河海大学学报(自然科学版),2002,30(6):52-55.(CHEN Bin,LIU Ning,ZHUO Jia-shou.Prin-ciple of Maximum Entropy for Back Analysis in Geotech-nical Engineering[J].Journal of Hohai University(Natu-ral Sciences),2002,30(6):52-55.(in Chinese))
[5] 邓 建,李夕兵,古德生.岩石力学参数概率分布的信息熵推断[J].岩石力学与工程学报,2004,(13):2177-2181.(DENG Jian,LI Xi-bing,GU De-sheng.Probability Distribution of Rock Mechanics Parameters by Using Maximum Entropy Method[J].Chinese Journal of Rock Mechanics and Engineering,2004,(13):2177-2181.(in Chinese))
[6] 顾冲时,汪自力,刘成栋.堤防工程安全评估专家赋权模型[J].岩土力学,2006,27(12):2100-2104.(GU Chong-shi,WANG Zi-li,LIU Cheng-dong.Experts’Weight Model Assessing Embankment Safety[J].Rock and SoilMechanics,2006,27(12):2100-2104.(in Chi-nese))
[7] 何金平,李珍照,施玉群.大坝结构实测性态综合评价中的权重问题[J].武汉大学学报(工学版),2001,34(3):13-17.(HE Jin-ping,LIZhen-zhao,SHIYu-qun.Weight Issue about Comprehensive Evaluating Dam Safety Monitoring Behavior[J].Journal of Wuhan University of Hydraulic and Electric Engineering,2001,34(3):13- 17.(in Chinese) )
(编辑:曾小汉)
Experts’Fuzzy Weight M odel of Dam Health Assessment Based on M aximum Entropy
YANG Yang1,2,FANG Chun-hui2,LIZhan-chao1,2,QIN Dong1,2
(1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University,Nanjing 210098,China;2.National Engineering Research Center ofWater Resource Efficient Utilization&Engineering Safety,Hohai University,Nanjing 210098,China)
In the period of dam operation,the dam structure is suffering from complex external environment influ-ence,and presents characteristics such as high correlation degree of qualitative and quantitative factors,a lot of missing and fuzzy uncertainty.By using the fuzzy mathematical theory the coefficients of experts’fuzzy weight on dam health assessment are constructed,and based on this,the fuzzy weight coefficient is optimized with GA algo-rithm according to themaximum entropy principle.Themulti-level experts’fuzzy weightmodel of dam health as-sessment is formed.Finally,the Xin’anjiang dam is selected as an evaluation example,the deformation,seepage,stress and strain and other aspects are assessed and the comprehensive assessment results are formed.The example further confirms the proposed model and has obtained good results.
dam;health;maximum entropy;expertweight;fuzzymathematics
TV698.1
A
1001-5485(2011)03-0020-04
2010-04-21
国家自然科学基金(51079046,50909041,50809025,50879024);国家科技支撑计划(2008BAB29B03,2008BAB29B06);中国水电工程顾问集团公司科技项目(CHC-KJ-2007-02);河海大学水文水资源与水利工程科学国家重点实验室专项基金(2009586012,2009586912,2010585212);中央高校基本科研业务费项目(2009B08514,2010B20414,2010B01414,2010B14114)
杨 阳(1985-),男,陕西西安人,博士研究生,主要从事水工建筑物结构安全监控研究与应用,(电话)025-83786957(电子信箱)dyhhu@qq.com。
