基于试验和有限元法获取滑面强度参数

张海平，任光明，王 军，陈全明，周维超

基于试验和有限元法获取滑面强度参数

张海平，任光明，王 军，陈全明，周维超

（成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059）

在滑坡稳定性计算和工程设计中滑带土的内聚力（C）和内摩擦角（φ）取值对工程至关重要。首先采用有限元法，对滑带土进行应力仿真分析，再结合滑带土室内试验的相关物性指标及强度特征，得到滑动面的强度参数，其结果与室内直剪试验所得到的滑带土强度参数值以及刚体极限平衡法反演得到的参数值十分接近。该方法不仅可作为该滑坡稳定性计算参数选取的合理依据，也可以作为获取滑动面强度参数的另一种行之有效、缜密而又合理的新方法。

内聚力；内摩擦角；有限元法；应力仿真分析；强度参数

1 概 述

用有限元方法分析土坡稳定问题是近年来土坡稳定分析研究的新趋势［1］。与目前常用的极限平衡法相比，有限元方法主要有以下优点：①可以考虑土体的非线性本构关系；②适用于任意复杂的边界条件，比如复杂的几何形状、有结构物作用、有支护的基坑等，而用其他方法很难解决［2］。目前，确定滑带土抗剪强度参数（C，φ）值的方法有试验、工程类比和反演分析3种［3］。滑带土剪切试验分为现场和室内2种，受试样和试验条件的限制，滑带土试验数据通常很离散，需要进行分析计算来确定［4，5］。反演分析是确定滑带土抗剪强度参数的一种有效的方法，根据滑坡的宏观变形状况假设滑坡的稳定性系数，再反算滑带土抗剪强度参数。反算是滑坡稳定性计算的逆过程，得到的参数更符合滑坡的变形情况，若没有试验数据时，可以直接作为稳定性计算、工程设计的参数［6－9］。目前，滑带土抗剪强度参数反演分析的方法一般分为单参数反演和双参数反演2种［10］。前者假定一个参数已知的前提下，反算另外一个参数，通常选择对滑坡稳定性影响较敏感的作为未知参数［11］。后者在反演中有2个未知的参数，通常选择2个距主滑动面等距的剖面建立极限平衡方程求解。

本文以黄河上游某水电站一滑坡为依托，通过对该滑坡的现场勘查，针对该滑坡稳定性计算中滑动面的强度参数选取问题，在选取典型地质剖面、建立地质概化模型的基础上，采用弹塑性Mohr-Cou-lomb理论对该滑坡滑体的法向应力进行有限单元法数值模拟，得出滑体正应力的分布状态及大小，结合室内相关试验成果，进而可获得该滑坡滑带土的抗剪强度参数。此种获取滑面强度参数的方法相比前述2种参数反演方法更为简练，且精确度高，为滑带土强度参数的选取提供了合理、可靠的理论依据。

2 工程实例

2．1 工程概况

该电站位于黄河上游河段，属高山峡谷地貌。此滑坡位于该电站坝址区上游的右侧，地形较陡，平均坡度约40°。地层岩性主要为三叠系下统（T1b）砂岩与板岩、粉砂质板岩、钙质板岩互层。区内断裂发育，地下水类型主要为基岩裂隙水和孔隙性潜水。该滑坡纵向长约495 m，横向宽度约115 m，前缘高程3 030 m，后缘高程3 342 m，主滑方向为NW348°，总体积约217．65万m3，为一大型岩质滑坡，图1是该滑坡的工程地质剖面图。

2．2 研究思路

（1）借助有限元法，选取该滑坡相关剖面来计算因滑体自重而在滑面上产生的正应力［12］。

（2）计算出正应力后，再结合室内相关的试验成果，可以得出一系列拟合关系式，最终推导出滑坡滑动面的强度参数。

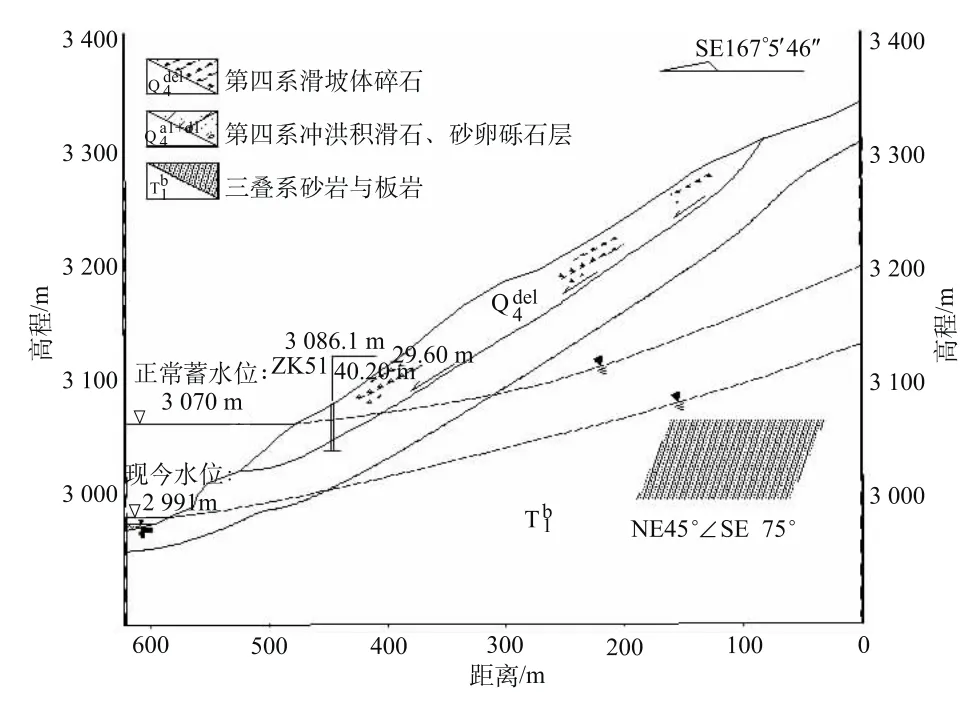
图1 滑坡工程地质剖面图Fig．1 Engineering geological profile of the landslide

（3）通过有限元法得到的滑面强度参数，经与传统的刚体极限平衡法反演得来的滑面参数进行对比，最终验证有限元法获取滑面强度参数的可行性。

3 模型的建立及关系式的拟合

3．1 坡体正应力的计算

根据现场的工程地质条件以及计算模拟的主要目的，来获得因滑体自重而在滑面上产生的正应力。计算模型如图2，定义材料本构关系为弹塑性，滑带作为节理单元，相关材料参数是在结合试验以及坝址区可行性研究报告建议的岩土体物理力学性质的基础上综合确定的。获得的滑面不同地段的正应力如图3。从图中可以看出，滑带受上覆岩土体自重的作用，其法向应力中上部及前缘部位较小，中下部较大，应力最高可达1．38 MPa。

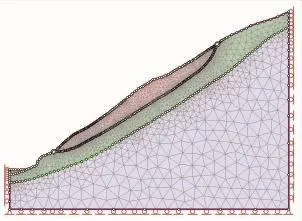
图2 坡体应力计算模型Fig．2 The computationalmodel of slope stress

3．2 拟合关系式的建立

3．2．1 滑带土的物性指标及其强度特征

拟合关系式的建立，是以室内相关试验成果作为基础的。通过对滑坡滑动面试样的室内试验，获得的滑带土原状样（三组）的物理性质测试结果如表1，通过比重试验获得滑带土的相对密度均值为2．74。

图3 滑面上正应力分布图Fig．3 Normal stress distribution of slipping surface

表1 滑坡滑带土原状样的物理指标Table 1 Physical index of sliding zone soil in the original state

为了进一步研究滑带土强度参数随含水率的变化规律，在室内将试样（以第①组试样为例）制成较天然含水率稍高、稍低的多个试样开展剪切试验，得到不同含水率、干密度试样的摩擦系数和内聚力（如表2），由此确定滑带土样在天然含水率状态下的力学参数C＝68．5 kPa，f＝0．466。根据表2中的滑带土的强度参数值C，f建立的其与状态指标（W／Wp）间的关系，表现出二者具有良好的相关关系（图4、图5），其拟合方程如下：

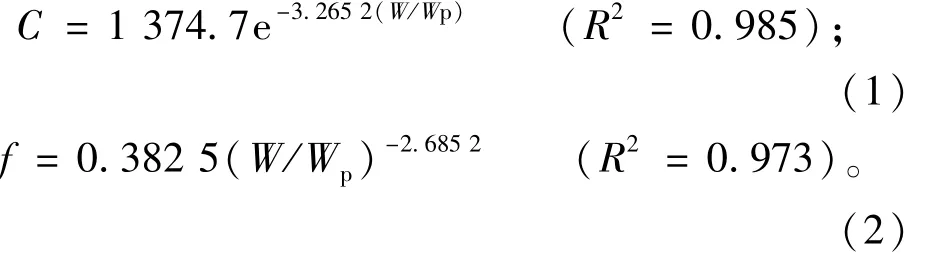
表2 不同含水率条件下的摩擦系数f和内聚力CTable 2 The value of friction＆cohesion in differentmoisture content

3．2．2 正应力与孔隙比的拟合关系

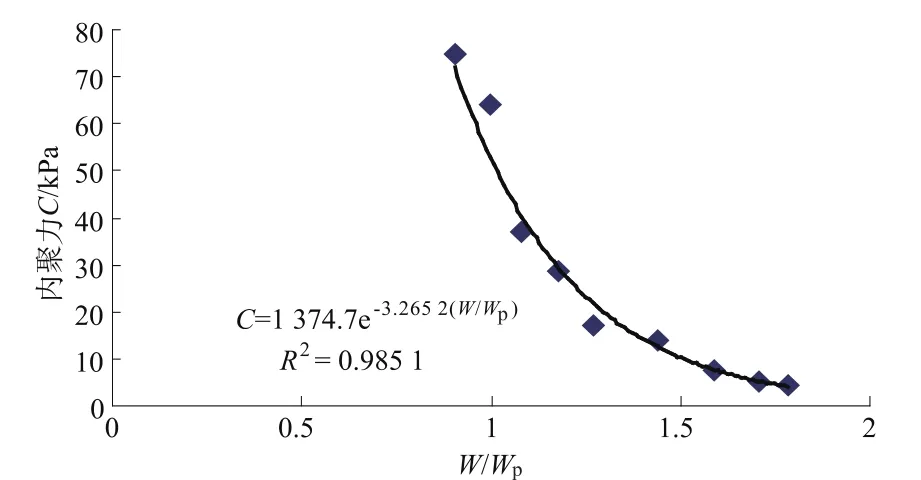
图4 滑坡基本值C与W／Wp的关系拟合曲线Fig．4 Fitting curve of the relation of C＆W／Wp

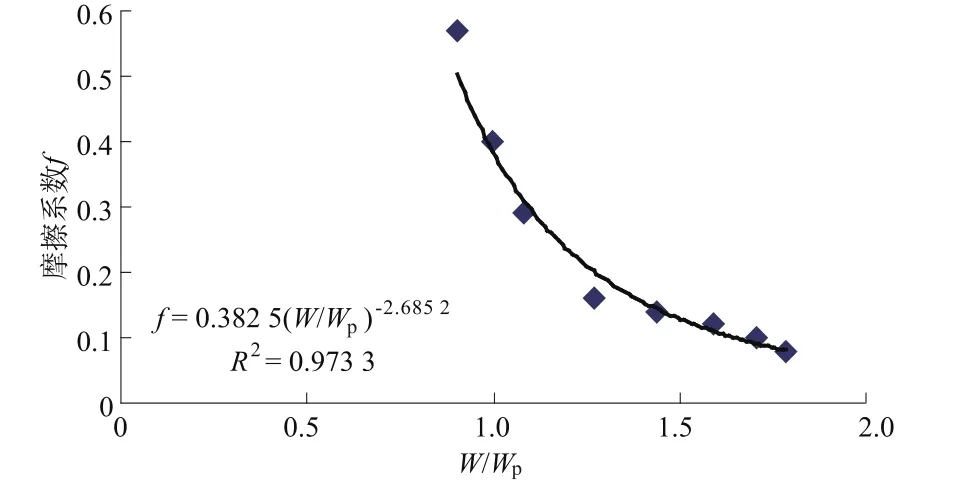
图5 滑坡基本值f与W／Wp的关系拟合曲线Fig．5 Fitting curve of the relation of f＆W／Wp

滑带土的物理力学性质与其所受的应力状态有明显的关系，且在上覆沉积物的重力作用下发生脱水、压密、固结，孔隙比随深度增大而减小的规律［13］。在室内将滑带土（以第①组试样为例）调制成液限状态或接近液限状态，放入压缩仪中进行逐级加压，获得不同压力下滑带土的孔隙比（表3），然后建立模拟压密滑带土的孔隙比与压力的关系式曲线如图6，所得试样的拟合方程

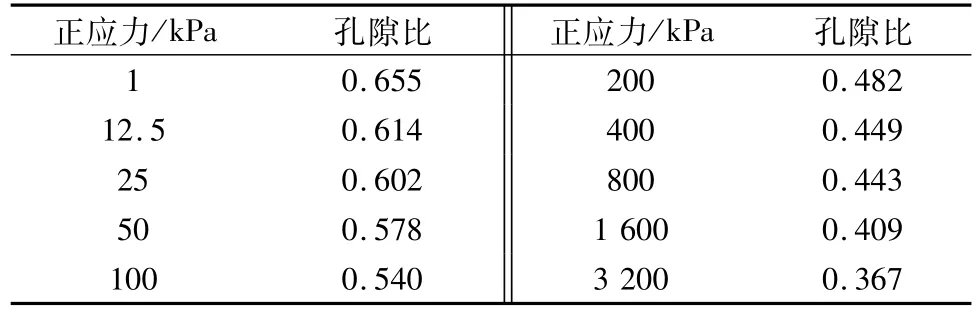
表3 各级正应力下的相应孔隙比Table 3 The value of void ratio in different normal stress

4 参数的获取及结果论证

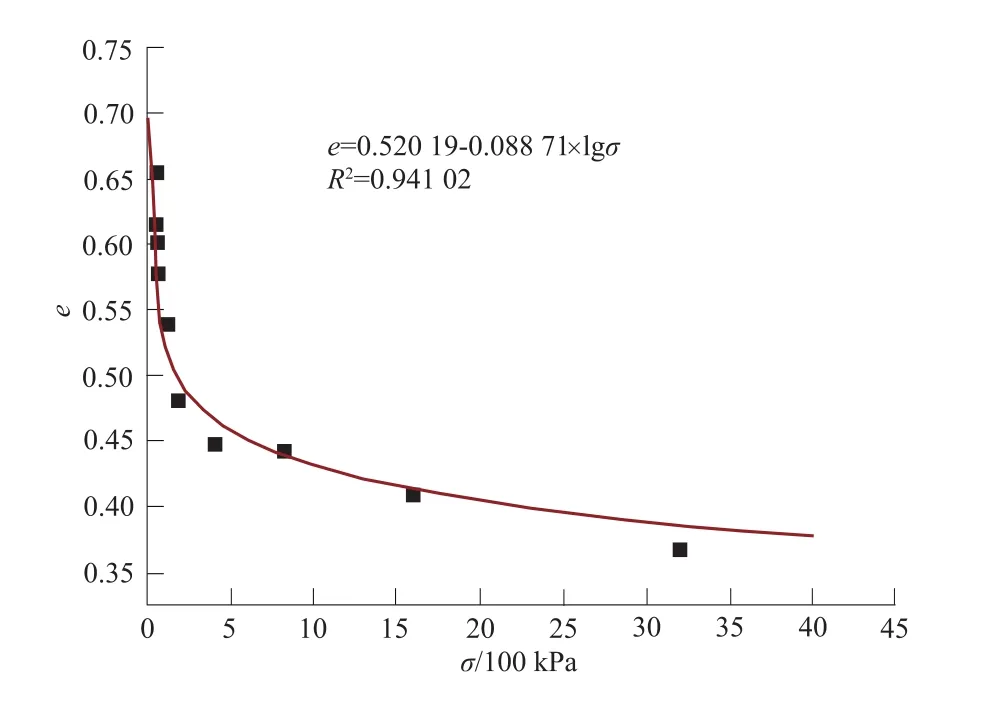
图6 滑坡试样e－σ关系曲线图Fig．6 Fitting curve of the relation of e＆σ

通过上述有限元模型对坡体应力进行计算，可以得到滑体因自重在滑面上产生的正应力，用获得的滑面正应力及重力压密试验建立的压力-孔隙比关系式（3），可以获得滑面不同地带的孔隙比，结合该滑坡的实际情况以及3组滑带土原状样试验结果，利用孔隙比与含水率、饱和度以及密度值之间的关系，可计算出坡体各个局部的含水量。根据试样建立的摩擦系数f、内聚力C与W／Wp的关系式（1），（2），计算出不同地段的f，C值（如表4）。假定滑带土为天然条件下的饱和度，从表4可以看出，利用有限元法计算的作用于滑面上的正应力以及根据试验建立的滑带土与含水量的关系，获得的滑面的标准摩擦系数为0．466，内聚力为72．03 kPa，与滑带土室内剪切试验所得出结果C＝68．5 kPa，f＝0．466相当接近，且与刚体极限平衡法所反演得来的强度参数C＝75 kPa，f＝0．462其吻合程度也是很好的。

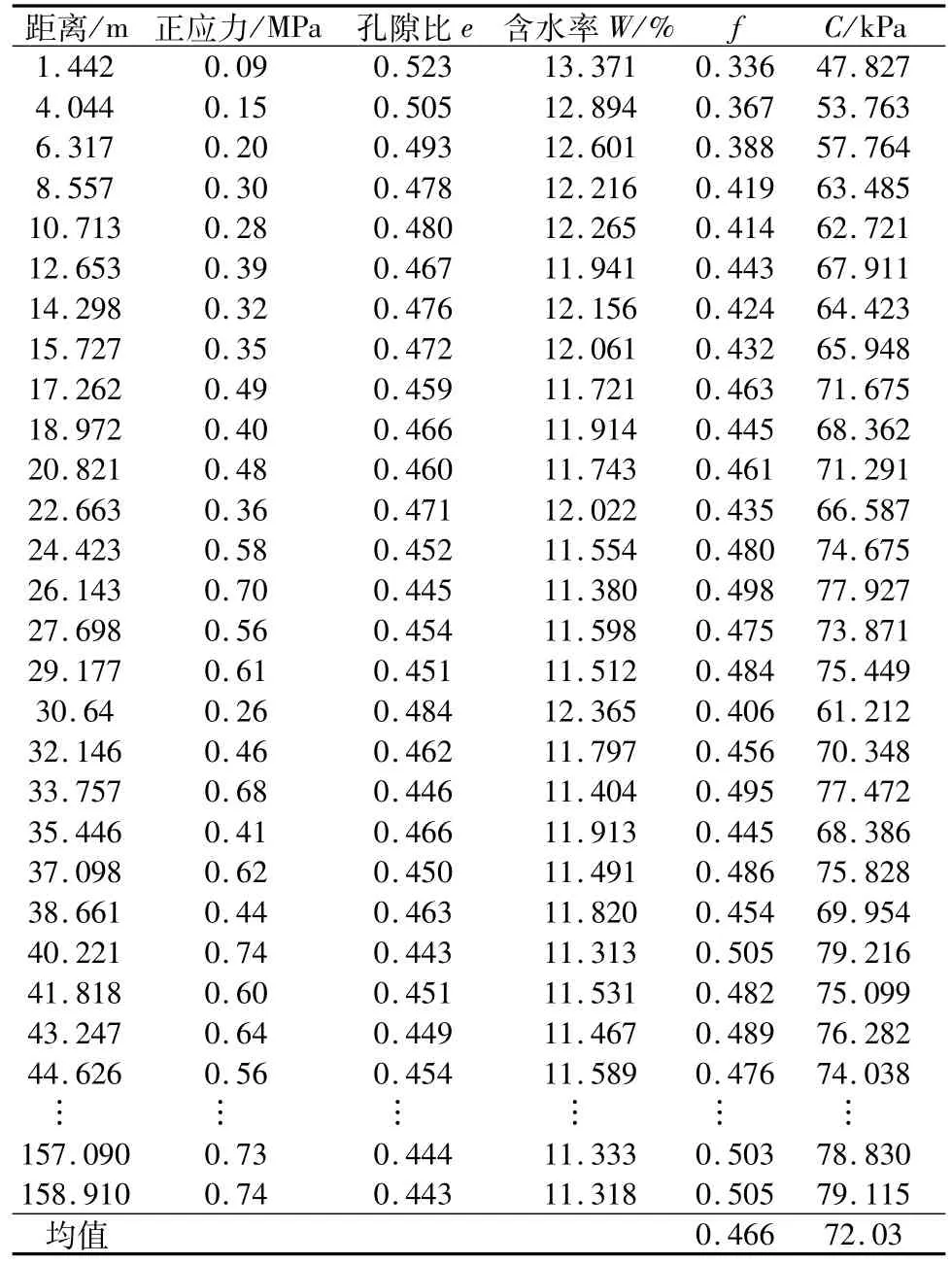
表4 应力分析获得的滑动面孔隙比、含水量及强度参数值Table 4 Void ratio＆moisture＆strength parameters of the slipping surface acquired by stress analysis

5 结 论

（1）细致的野外现场勘查是进行滑坡稳定性评估及其计算的前提。滑动面强度参数的选取直接关系到滑坡稳定性计算的正确性与合理性。选取合适的计算剖面，建立计算模型，对滑面参数进行反演以及坡体稳定性计算很有必要性。

（2）通过有限元法对坡体进行应力仿真分析，检验了本文对滑面强度参数反演方法的可行性。

（3）通过室内土工试验，准确获得滑带土的物性指标及强度特征，是建立相关拟合关系式的关键。

（4）该方法较之于传统的参数反演方法更为简练，也为滑面强度参数的选取提供了有力的理论依据，可以推广至其它滑坡甚至岩质边坡潜在滑动面的强度参数反演中去。

［1］ Duncan，State of the art：Limit Equilibrium and Finite-El-ement Analysis of Slopes［J］．Journal of Geotechnical Engineering，1996，122（7）：577－595．

［2］ 史恒通，王成华．土坡有限元稳定性分析若干问题探讨［J］．岩土力学，2000，21（2）：152－155．（SHIHong-tong，WANG Cheng-hua．Some Problems in Finite Ele-ment Analysis of Slope Stability［J］．Rock and Soil Me-chanics，2000，21（2）：152－155．（in Chinese））

［3］ 周平根．滑带土强度参数的估算方法［J］．水文地质工程地质，1998，（6）：30－34．（ZHOU Ping-gen．The Esti-mate Method of Parameter of Slide Zone Soil［J］．Hydro-geology＆Engineering Geology，1998，（6）：30－34．（in Chinese））

［4］ 林鲁生，蒋 刚，白世伟，等．土体抗剪强度参数取值的统计分析法［J］．岩土力学，2002，23（5）：570－574．（LIN Lu-sheng，JIANG Gang，BAI Shi-wei．Statistical Analysis Method of Taking Value for Shear Strength Pa-rameters of Soil Mass［J］．Rock and Soil Mechanics，2002，23（5）：570－574．（in Chinese））

［5］ 徐建平，胡厚田，张安松，等．边坡岩体物理力学参数的统计特征研究［J］．岩石力学与工程学报，1999，18（4）：382－386．（XU Jian-ping，HU Hou-tian，ZHANG An-song，et al．On Statistical Characteristics of Physical and Mechanical Parmeters in Slope Rockmass［J］．Chi-nese Journal of Rock Mechanics and Engineering，1999，18（4）：382－386．（in Chinese））

［6］ 高德军，徐卫亚，郭其达．长江三峡大石板滑坡计算参数反分析［J］．河海大学学报（自然科学版），2006，34（1）：74－78．（GAO De-jun，XU Ya-wei，GUO Qi-da． Back Analysis of Calculation Parameters for Dashiban Landslide at Three-Gorges Reservoir on Yangtze River［J］．Journal of Hohai University（Natural Sciences），2006，34（1）：74－78．（in Chinese））

［7］ 彭亚明，彭军还，张 彬，等．三峡库区某滑坡抗剪强度参数的反演分析［J］．桂林工学院学报，2003，23（3）：279－283．（PENG Ya-ming，PENG Jun-huan，ZHANG Bin，et al．Reversion Analysis of Anti-shearing Strength Parameters of A Landslide in TGPReservoir Are-a［J］．Journal of GuiLin Institute of Technology，2003，23（3）：279－283．（in Chinese））

［8］ 富凤丽，佴 磊，李广杰，等．中里滑坡反分析及强度系数取值研究［J］．长春科技大学学报，2000，30（2）：165－169．（FU Feng-li，NAI Lei，LIGuang-jie，et al．The Anti-analysis of Zhongli Landslide and A Study on Determining the Values of Strength Parameters［J］．Jour-nal of Changchun University of Science and Technology，2000，30（2）：165－169．（in Chinese））

［9］ 李端有，甘孝清．滑坡体力学参数反分析研究［J］．长江科学院院报，2005，22（6）：44－48．（LI Duan-you，GAN Xiao-qing．Mechanical Parameter Back Analysis of Landslide［J］．Journal of Yangtze River Scientific Re-search Institute，2005，22（6）：44－48．（in Chinese））

［10］柴 波，殷坤龙，简文星．滑坡计算参数反算分析的优化算法［J］．武汉理工大学学报，2007，29（11）：98－102．（CHAI Bo，YING Kun-long，JIAN Wen-xing．The Optimize Method of Parameter of Slide Zone Soil［J］．Journal of Wuhan University of Technology，2007，29（11）：98－102．（in Chinese））

［11］徐汉斌，王 军．反算法中滑坡稳定系数的取值问题［J］．四川地质学报，1999，19（1）：86－89．（XU Han-Bing，WANG Jun．Selection of Landslide Stability Factor in Inverse Calculation［J］．Journal of Sichuan Geology，1999，19（1）：86－89．（in Chinese））

［12］张倬元，王士天，王兰生．工程地质分析原理［M］．北京：地质出版社，1993．（ZHANG Zhuo-yuan，WANG Shi-tian，WANG Lan-sheng．Principles of Engineering Geology［M］．Beijing：Geologic Publishing House，1993．（in Chinese））

［13］聂德新，任光明，左三胜．用重力压密原理评价大型滑坡滑面强度参数算法［J］．地质灾害与环境保护，1996，7（1）：7－12．（NIE De-xin，REN Guang-ming，Zuo San-sheng．Study on Strength Parameter of Slide Zone Soil with The Principle of Gravity Compaction of Sedi-ments［J］．Journalof Geological Hazards and Environment Preservation，1996，7（1）：7－12．（in Chinese） ）

（编辑：刘运飞）

Acquisition of Sliding Surface’s Strength Parameters Based on Experiment and Finite Element M ethod

ZHANG Hai-ping，REN Guang-ming，WANG Jun，CHEN Quan-ming，ZHOUWei-chao
（National Laboratory of Geohazards Prevention and Geo-Environment Protection，Chengdu University of Technology，Chengdu 610059）

In the landslide stability calculation and engineering design，it is very important to get the right value of cohesion（C）and internal friction angle（φ）for the sliding zone soil．Firstly，this paper uses the finite elementanaly-sismethod to conduct stress simulation analysis of the landslide slope．Then，by adopting related physical index and intensity properties of laboratory testing indicators of sliding zone，it can invert the strength parameters of the slipping surface，and the inversion results are very close to the value of indoor direct shear test of the sliding zone soil strength parameters．It provides a reasonable basis for the calculation of landslide stability in the selection of parameters，ital-so proposed a well-established，and more carefulmethod for the inversion strength parameters of sliding surface．

cohesion；internal friction angle；finite elementmethod；stress simulation analysis；strength parameters

TU443

A

1001－5485（2011）03－0045－05

2010-03-28

张海平（1984-），男，湖南冷水江人，硕士研究生，主要从事地质工程的研究，（电话）13882207315（电子信箱）Zsail2010＠163．com．