渡槽内流速对其结构静力响应的影响分析

徐梦华，莫海鸿

渡槽内流速对其结构静力响应的影响分析

徐梦华，莫海鸿

（华南理工大学土木与交通学院，广州 510640）

采用三维有限元模型，通过对比计算，研究了渡槽内流速对其横、竖向结构静力响应的影响。研究表明：流速对渡槽横向位移以及横向弯矩的静力响应虽然有比较明显的影响，且随着槽内流速的增大，影响也在加大，但是，在1．0～2．5 m／s的流速范围内，影响很小，不会产生危害；高流速对渡槽竖向位移以及竖向弯矩影响要比低流速大，但是，在1．0～2．5 m／s的范围内，对渡槽的竖向位移及竖向弯矩的影响也很有限。

渡槽；流速；静力；响应

1 概 述

渡槽设计时，根据尽量减小水头损失的要求，渡槽内的平均流速一般规定在1．0～2．5 m／s的范围内［1］。在以往对渡槽结构的流固耦合分析研究中［2－6］，无论是试验研究还是计算分析，都是针对槽内水流速为零的情况，也就是不考虑流速的影响，这一方面是受到试验和计算条件的制约，因为在试验中给渡槽加上纵向流速条件不仅是难度较大，而且需要的试验成本也会大幅提高。在数值模拟计算方面，三维有限元模型计算规模过大，再加上纵向流速的条件，进一步加大计算难度，一般计算机条件难以完成；另一方面，现有的各种简化模型都是针对无流速情况的，无法模拟有流速的渡槽。但实际上渡槽在有水的情况下，一般都处于渡槽在输水的工作状态，是有相应流速存在的。因此，在这种背景下，探明在有流速的情况下，渡槽结构的流固耦合响应特点，以及流速的影响大小，一方面为渡槽在有流速情况下的结构分析提供依据，同时也为现有的各种简化计算模型以及模型试验是否该提供反映流速因素的参照，是非常有意义的。

本文拟就槽内流速对渡槽流固耦合静力横、竖向响应的影响开展研究，计算中采用三维流固耦合有限元方法，在高性能计算机上采用多核并行，用大型有限元软件ADINA来完成三维流固耦合有限元的计算。

2 渡槽三维流固耦合有限元模型［4］

2．1 结构部分的动力控制方程

结构部分的动力控制方程如下，

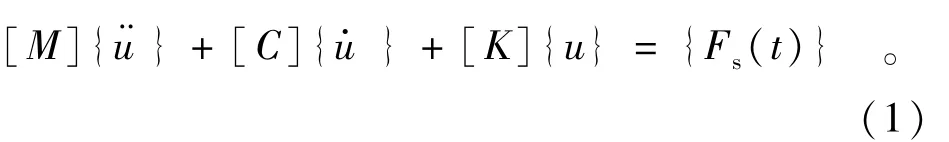
2．2 流体域控制方程

在一般情况下，流体域的求解采用的是欧拉描述，但是当求解区域存在自由液面或者随结构运动而运动的流固耦合边界时，就必须采用拉格朗日描述来跟踪边界的运动，从而欧拉描述的坐标系不再是固定区域，而是在不断变化的区域，但是在整个流体区域内，仍是采用欧拉描述来求解流体域的方程，此即为任意拉格朗日－欧拉描述（ALE描述）。已有的研究表明，ALE运动学描述非常适用于求解含自由液面的液体大幅晃动问题［7，8］，任意拉格朗日描述下的N-S方程和连续性方程为式中：ρ为质量密度；u为位移，和分别为对时间的一阶和二阶导数；a为对流速度为材料的运动速度为欧拉网格的运动速度；f为外界施加力，对于耦合界面上节点，f包括耦合力，τ为流体的应力张量。

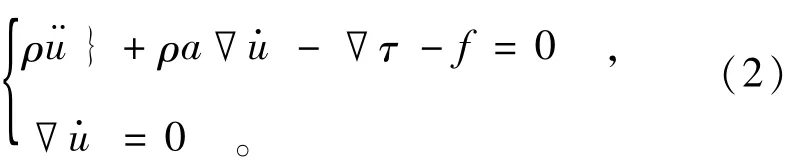
2．3 流体自由液面

渡槽中水体的自由液面S（xi，t）在这里是不穿透边界，需要满足下面的运动边界条件和动力边界条件：

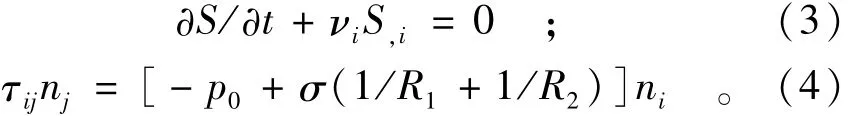
式中：νi为液面的速度向量；p0为外界施加在自由液面的压力；σ为表面张力；ni为自由液面的单位法向量；R1和R2为自由液面曲面在两个水平坐标轴方向的曲率半径。

2．4 耦合条件

槽身内水体和槽身通过相互作用面进行耦合，耦合边界面上速度和相互作用是连续的，满足以下连续条件：

式中：sf和ss分别为耦合面上水体和槽体结构的应力；nf和ns分别为水体和槽体结构耦合面的法向量，方向向外。

3 流固耦合分析

以东深供水大跨度U型简支渡槽的某段为例，见图1。该段的结构特征与参数为：主跨长24 m，U型内断面，侧壁厚30 cm，槽底厚75 cm，槽顶设有截面为矩形的拉杆（宽×高＝40 cm×50 cm，间距2 m），两端为简支。槽墩尺寸为宽×高×厚＝7 m×15 m×1 m。

图1 大跨度简支渡槽及槽身截面尺寸Fig．1 Large-span sim ply supported aqueduct and its section

力学参数取值如下。

槽身钢筋混凝土：混凝土强度等级C40，密度2 450 kg／m3，弹性模量35．00 GPa，泊松比0．167；

槽墩钢筋混凝土：混凝土强度等级为C25，密度2 450 kg／m3，弹性模量28．00 GPa，泊松比0．167；

水体：密度1 000 kg／m3，粘滞系数0．001 05 kg／m2·s，为不可压缩液体，槽内设计水深4．7 m。

本次计算中分别取1．0，1．5，2．0，2．5，3．0 m／s流速，并与流体静止（0．0 m／s）时静力状态下的计算结果进行对比分析流速的影响。槽身跨中截面底部中点（4＃，见图1）侧移以及槽身跨中截面的水平向弯矩过程线对比分别见图2、图3。

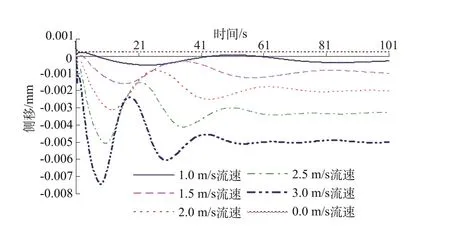
图2 槽身跨中截面底部中点侧移过程线Fig．2 Lateral displacement hydrograph of them id-point at the bottom of them id-section of the aqueduct body

图3 槽身跨中截面的水平弯矩过程线Fig．3 Horizontalmoment hydrograph of them id-cross-section of the aqueduct body

由图2、图3可以看出，槽内水的流速对渡槽槽身跨中截面的侧移以及弯矩有比较明显的影响，随着槽内流速的增大，影响也在加大。虽然流速使侧移和水平向弯矩增加，但是侧移和水平向弯矩的数值本身很小，并且振幅也很小。因此在限定的1．0～2．5m／s的范围内，在没有地震荷载作用下，流速对渡槽侧移和水平向弯矩的影响不会产生过大的危害。

槽身跨中截面底部中点（4＃，见图1）竖向位移以及槽身跨中截面的竖向弯矩过程线对比分别见图4、图5。

图4 槽身跨中截面底部中点竖向位移过程线Fig．4 Vertical displacement hydrograph of them id-point on the bottom of them id-section of the aqueduct body

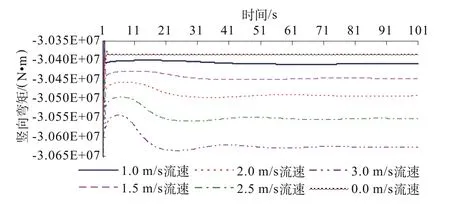
图5 槽身跨中截面的竖向弯矩过程线Fig．5 Verticalmom ent hydrograph of them id-cross-section of the aqueduct body

由图4、图5可以看出，槽内水体在高流速时对渡槽槽身跨中截面竖向移以及竖向弯矩影响要比低流速大，但是各个流速情况下渡槽的竖向位移及竖向弯矩振动都很小；在槽内1．0～2．5 m／s的平均流速范围内，竖向位移的增加值在0．003～0．017 mm之间，增加幅度为0．08%～0．52%；竖向弯矩的增加值在2．321 04～1．691 05 kN·m，增加幅度为0．08%～0．55%。由此可见，流速对竖向位移以及竖向弯矩的影响也很有限。

4 结 论

本文采用三维有限元方法，通过对比计算，分析了大型渡槽内的流速对渡槽静力响应的影响，主要得到以下结论：

（1）槽内水的流速对渡槽槽身跨中截面的结构静力侧移以及结构静力弯矩有比较明显的影响，随着槽内流速的增大，影响也在加大。虽然流速使侧移和水平向弯矩增加，但是由于侧移和水平向弯矩的增加幅度很小，因此在1．0～2．5 m／s的设计流速范围内，流速对渡槽结构的水平向安全及稳定不会产生危害。

（2）槽内水体在高流速时对渡槽槽身跨中截面竖向位移以及竖向弯矩影响要比低流速大，但是在槽内平均流速为1．0～2．5 m／s的范围内，竖向位移的增加值在0．003～0．017 mm之间，增加幅度为0．08%～0．52%；竖向弯矩的增加值在2．32×104～1．69×105kN·m，增加幅度为0．08%～0．55%。由此可见，流速对竖向位移以及竖向弯矩的影响也很有限。

［1］ 竺慧珠，陈德亮，管枫年．渡槽［M］．北京：中国水利水电出版社，2005．（ZHU Hui-zhu，CHEN De-liang，GUANG Feng-nian．Aqueducts［M］．Beijing：ChinaWa-ter Power Press，2005．（in Chinese））

［2］ 徐建国．大型渡槽结构抗震分析方法及其应用［D］．大连：大连理工大学，2005．（XU Jian-guo．Method and Application of Aseismic Analysis for Large-Scale Aque-duct［D］．Dalian：Dalian University of Technology，2005．（in Chinese））

［3］ 张述琴，张 晖．刁河板粱式渡槽仿真模型试验研究［J］．长江科学院院报，2002，19（9）：75－77．（ZHANG Shu-qin，ZHANG Hui．Emulation Model Test of Plank-beam Style Aqueduct of Diaohe River［J］．Journal of Yangtze River Scientific Research Institute，2002，19（9）：75－77．（in Chinese））

［4］ 吴 轶．大型梁式渡槽地震反应分析及设计方法研究［D］．广州：华南理工大学，2004．（WU Yi．Study on Seismic Response and Design Method of Large Beam Aq-ueduct［D］．Guangzhou：South China University of Technology，2004．（in Chinese））

［5］ 王 博．大型渡槽结构地震反应分析理论与应用［D］．上海：同济大学，2000．（WANG Bo．Theory and Application of Earthquake Response Analysis for Large-scale Aqueduct［D］．Shanghai：TongjiUniversity，2000．（in Chinese））

［6］ 张俊发，刘云贺，王 颖，等．渡槽-水体系统的地震反应分析［J］．西安理工大学学报，1999，15（4）：46－51．

（ZHANG Jun-fa，LIU Yun-he，WANG Ying，et al．A Seismic Response Analysis of Water-Aqueduct-Pier Sys-tem［J］．Journal of Xi’an University of Technology，1999，（4）：46－51．（in Chinese））

［7］ LIU W K．Finite Element Procedure for Fluid-Structure Interactions and Application to Liquid Storage Tanks［J］．Nuclear Engineering and Design，1981，65：221－238．

［8］ HIRT G W，AMSDEN A A，COOK J L．An Arbitrary Lagrangian-Eulerian Computing Method for All Flow Speeds［J］．J．Comp Phys，1974，14（3）：227－253．

（编辑：赵卫兵）

Analysis on Influence of Fluid Velocity on Static Force Responses of Aqueduct

XU Meng-hua，MO Hai-hong
（School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510640，China）。

The influences of fluid velocity on lateral and vertical static force responses of aqueductwere studied by contrast calculation using three-dimensional finite elementmodel．The results show that although the influence of fluid velocity on lateral displacement and moment of the aqueduct is evident and increases with fluid velocity，yet within a velocity range of 1．0－2．5 m／s the influence is limited．The influence of high fluid velocity on vertical displacement and moment is larger than that under low velocity．However，in a range of1．0－2．5 m／s，the influ-ence can be negligible．

aqueduct；fluid velocity；static force；response

TV314

A

1001－5485（2011）03－0059－04

2010-03-30

徐梦华（1972-），男，河南淮滨人，博士，讲师，主要从事水工结构抗震分析及大坝安全监测方面的研究，（电话）13729808934（电子信箱）mhxu＠scut．edu．cn。