基于支持向量机的汽车曲轴质量诊断模型
2011-09-05何曙光赵永满
赵 凯,何 桢,何曙光,赵永满
(天津大学 管理与经济学部,天津 300072)
0 引言
多元质量控制的概念最早是由Hotelling于1947年提出的。多元质量控制与一元质量控制类似,一般都要求质量特性服从正态分布,多元质量控制是基于多元正态分布建立检验统计量进行质量控制的。多元统计过程控制(MSPC)是多元质量控制常用的方法,它通过监控生产过程中多个相关变量,以探测过程可能发生的异常,达到提高产品质量的目的。当前MSPC技术应用中存在的主要问题是,随着过程变量维数的增加,监控系统的复杂性急剧增加,而变量间的多重共线性又给过程的异常诊断带来了困难。由于多元过程质量特性之间存在相关性,上述多元质量控制方法难以确定过程变异的来源,即当控制图报警时,如何判定变异是哪一个或哪几个质量特性的变动引起的。为了克服存在的这些问题,R.S.Guh[1](2007),Niaki et al.[2](2005),Hou et al.[3](2003),Yu( 2008;2009)[4;5],Venkat(2003)[6]等学者对该问题应用不同的方法进行了研究。本文将根据某企业汽车曲轴实际生产情况,应用基于支持向量机(SVM)的多元质量控制与诊断方法,结合企业现有MARPOSS综合测量机的测量数据,对产品的数据进行分析、处理、监测与诊断。
1 T2控制图
设某多元过程有p个关键质量特性,表示为X=(X1,X2,…,Xp),设每个样本的样本容量为n,共有m样本。进一步假设X服从多元正态分布,即X~Np(μ0,∑0),其中μ0和∑0分别为总体均值和方差-协方差矩阵。则Xij=(Xij1,Xij2,,…,Xijp)是p维向量,代表在第i个样本中第j个观测值的p维质量特性,其中i=1,2,…,m;j=1,2,…,n。Xij的第l成分Xijl表示第l个质量特性,其中l=1,2,…,p。假设Xij是相互独立且服从在过程受控状态下均值μ和协方差矩阵∑已知的多元正态分布。一般在实际生产过程中,总体均值μ和方差协方差矩阵∑是未知的,需要从过程受控时采集的初始样本中分析得到,用估计的样本均值向量和样本-协方差矩阵S代替μ和∑。样本均值向量为样本方差-协方差矩阵为:

则T2统计量定义为:
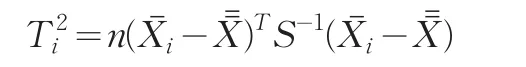
为第i个样本的均值向量,(⋅)T为转置操作。控制限为:

与一元控制图不同,多元控制图不但需要设计合理的统计量和控制限,而且在控制图报警后需要进一步识别导致控制图报警的变量/变量组合,即多元过程控制图的异常识别或诊断。
2 支持向量机原理
SVM是一种机器学习算法,其理论基础是Vapnik等提出的统计学习理论[8]。SVM是将原训练数据映射到较高的维,在该新的维上,搜索线性最佳分离超平面。对于二分类问题,设训练样本集D为(X1,y1),(X2,y2),…,(Xi,yi),其中i=1,2,…,l,l为训练样本数,Xi∈Rd为输入向量,yi∈{ }
+1,-1为输出分类标志。对于线性可分问题,可以用n维空间中的超平面WXT+b=0将训练样本集分开,其中W'=(w1,w2,…,wd)为d维向量且‖ ‖W=1,该平面称为分类超平面。显然对于训练样本集D,该分类超平面并不唯一,即存在一组与该超平面平行的超平面,均可以将训练样本集正确分开,把距离最大的两个超平面之间的距离称为分类间隔,则有:

此时最大边缘等于2‖W‖ ,是分类间隔最大等价于使‖W‖2最小。满足条件(1)并使‖W‖22最小的超平面称为最优分类超平面,相距最远的两个超平面上的点就称为支持向量。将该问题转化为其对偶问题,并采用Lagrange优化方法,得到的优化问题如(2)所示。

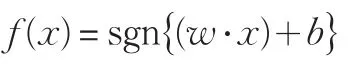
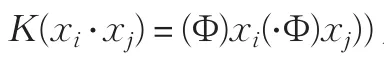
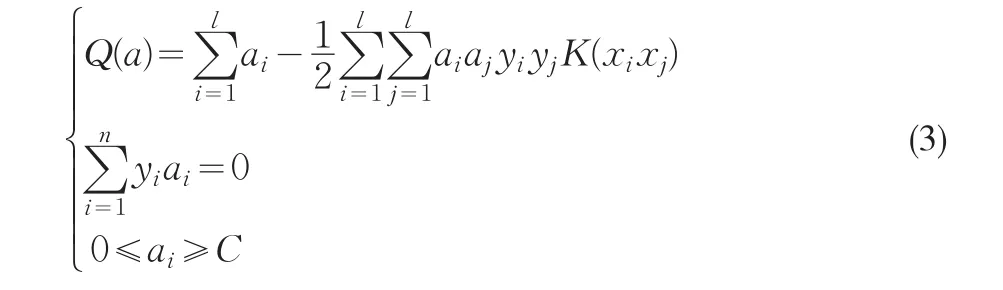
不同的核函数形式对应不同的算法,多项式核函数、高斯径向基核函数、B样条核函数等是最常用的核函数,其中高斯径向基核函数由于具有较强的非线性分类能力而得到广泛应用,其形式为:

其中,h2是核函数参数。
3 基于SVM的MSPC诊断模型
根据文献[7]基于SVM的MSPC诊断过程主要包括三个部分:MSPC过程,采用多元控制图,对制造过程中的多元质量特性进行监控;诊断模型训练,采用多元过程中的异常数据作为训练数据集,包括异常质量数据和对应的异常类别,其中异常类别根据导致报警的异常变量/变量组合进行编码;MSPC诊断,在所构建的诊断模型基础上,如果MSPC报警,则对过程进行诊断,以确定导致过程异常的变量/变量组合。
针对汽车曲轴生产过程实际问题,考虑加工过程的三个变量,即p=3,笔者构建诊断模型的过程为:
(1)明确过程输出特性及过程输出特性的具体要求,抽取生产过程曲轴的样本,利用多元过程控制图判明过程是否处于统计受控状态;通过构造伽马图,从图形的特征接受本文研究的曲轴生产过程的多元正态性;
(2)明确过程处于受控状态以及过程具有多元正态分布,计算多元过程能力指数,描述过程的能力;
(3)通过生产线MARPOSS综合测量机中获取的数据,计算样本均值向量Xˉ和样本方差-协方差矩阵S,用Xˉ和S估计总体的均值μ和协方差矩阵Σ;
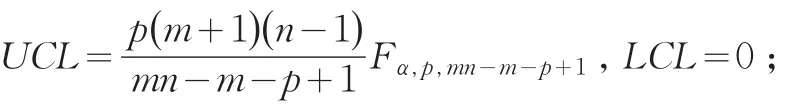
(5)用构建的T2控制图收集用于构建SVM模型训练和测试样本,根据生产的实际情况,对于每一种给定的均值偏移模式,产生50个超出T2控制限的曲轴生产数据,同时产生各不同模式的50个不超出T2控制限的曲轴生产数据;
(6)构建SVM模型。多元过程监控与诊断中,神经网络等方法在解决诊断问题时,是应用ANN相关模型拟合过程质量特性和变量偏移类别的分类模型,而随着问题维度的增加,分类的难度显著增加[7]。而SVM的理论基础是Vapnik等提出的统计学习理论,统计学习理论采用结构风险最小化原则,提高了模型的泛化能力,且得到的是全局最优解,可有效避免神经网络中的过学习问题,尤其适合于小样本学习问题。随着维度的增加,则异常组合数呈指数增长,如果用单一诊断模型,模型的输出维度太高,从而给模型的构建带来了很大的难度[7]。
本文建立的模型如图1所示,用上面产生的汽车曲轴加工过程中的数据,对模型进行训练。在MSPC诊断过程中,作者研究的变量p=3,每一个变量分为正常和异常两种情况,共有8种组合,其中包含受控状态1种和过程发生偏移的7种。在模型中,过程的每一变量分别应用一个SVM分类模型对各个变量是否存在均值偏移进行诊断,每个SVM分类器的输出为0或1,其中1代表该变量未发生均值偏移,0代表该变量均值发生偏移。在模型中,将所有3个变量均作为模型的输入。由于在对每一个变量的偏移进行诊断时,同时考虑了其他变量对该变量的影响,因此并不会忽略变量之间的相关性,而模型个数仅与过程质量特性个数相等;

图1 MSPC均值偏移诊断模型
(7)SVM模型的参数优化。SVM模型训练过程中,笔者选择高斯径向基函数作为SVM的核函数。通过仿真方法对模型的性能进行分析,确定在SVM模型中式(3)和式(4)中的惩罚参数C和核函数参数h2取值;
(8)具体应用。采用T2控制图进行监控,监控多元加工过程是否有报警;若出现报警点,则利用建立的SVM模型对报警信号进行诊断,判断均值偏移变量的组合模式,并解释其实际意义,从而实现多元过程均值偏移模式的诊断。
4 实例
笔者通过对某企业汽车曲轴生产的数据分析来加以说明SVM模型的应用。通常曲轴由多个主轴颈和多个连杆轴颈组成,用于描述曲轴质量的参数较多,包括主轴颈与连杆轴颈的轴径、圆度、圆柱度以及跳动度、冲程等。其中轴颈的直径与曲轴的冲程对整个曲轴性能有着关键性的作用,其中需要对曲轴的这三个质量特性进行控制,以满足产品的性能要求。本文选用某型号曲轴终检数据进行了实例研究,数据包括曲轴主轴颈直径X1、曲轴连杆轴径X2及该主轴颈与连杆轴径构成的曲轴的冲程X3。考虑到生产线的小时生产量、生产线的调整周期及稳定受控状态等,确定数据抽样方案。产生过程受控状态下的样本50个,过程均值发生偏移的样本350个,按比例作为模型训练和测试过程中的训练样本和测试样本。
通过MARPOSS综合测量机中大量的样本数据,计算过程受控时的样本均值向量Xˉ和样本方差-协方差矩阵S为:

这里假定生产过程中曲轴加工过程的样本方差-协方差矩阵S保持不变。
SVM模型训练过程中,选择的高斯径向基函数作为SVM的核函数。经过仿真优化得到在SVM模型中重要的参数,惩罚参数C=1200和核函数参数h2=2.9。

表1 SVM模型分类结果
应用所选择的参数,运用建立的SVM模型采集的数据进行处理,结果见表1。在所有7种变异模式中,其中有一个变量均值发生偏移时,分类的正确率最大为78%以上,三个变量均发生偏移时,分类的正确率为70%,该方法的总变异识别正确率为76%。将该结果与实际生产过程中的MARPOSS综合测量机相结合,能更好地解决生产现场中遇到的实际问题,为企业产品加工过程起到一定的指导和参考作用。
5 结论
目前,生产加工过程中需要同时控制多个变量,以使质量达到顾客的要求,由于多元过程质量特性之间存在相关性,从而给多元过程质量诊断带来的困难。本文根据对某企业汽车曲轴加工过程的调研,选取对其产品影响重要的几个质量特性,应用基于支持向量机的方法模型对产品质量特性的均值偏移情况进行了初步的应用研究,均值偏移只取了正常和便宜两种情况。通过实例表明,应用了基于SVM的多元质量控制与诊断方法,可以较好地识别多元加工过程中的均值偏移问题,在一定程度上解决了多重线性相关给异常诊断带来的困难,是对现有曲轴生产线MARPOSS综合测量机的一个补充应用研究。
[1]Guh,R.S.On-line Identification and Quantification of Mean Shifts in Bivariate Processes Using a Neural Network-based Approach[J].Quality and Reliability Engineering International,2007,(23).
[2]Niaki,S.T.A,Abbasi,B.Fault Diagnosis in Multivariate Control Charts Using Artificial Neural Networks[J].Quality and Reliability Engineering International,2005,(21).
[3]Hou,T.H.,Liu,W.L.LIN,L.Intelligent Remote Monitoring and Diagnosis of Manufacturing Processes Using An Integrated Approach of Neural Networks And Rough Sets[J].Journal of Intelligent Manufacturing,2003,(14).
[4]Yu,J.B.,Xi,L.F.,Zhou,X.Intelligent Monitoring And Diagnosis of Manufacturing Processes Using An Integrated Approach of KBANN And GA[J].Computer in Industry,2008,(59).
[5]Yu,J.B.,Xi,L.F.A Neural Network Ensemble-Based Model For On-Line Monitoring And Diagnosis of Out-Of-Control Signals in Multivariate Manufacturing Processes[J].Experts Systems with Applications,2009,36(1).
[6]Venkat Venkatasubramanian,R.R.Surya N Kavuri,Kewen Yin.A Review of Process Fault Detection And Diagnosis Part III:Process History Based Methods[J].Computers And Chemical Engineering,2003,(27).
[7]Vapnik V.N.The Nature of Statistical Learning Theory[M].New York:Springer,l 995.
[8]Cristianini,N.,J.Shawe-Taylor.支持向量机导论[M].李国正,王猛,曾华军译.北京:电子工业出版社,2007.
