基于区制转移模型的中国短期利率动态行为研究

蒋祥林，李一凡

(复旦大学 金融研究院，上海 200433）

0 引言

短期利率动态行为对固定收益证券和利率衍生品的定价起着十分重要的作用，了解短期利率的动态有助于金融产品价格发现和利率风险管理。在实际经济运行中，我国短期利率发生了显著的结构性变化，利率波动性发生了明显的分界。因此，有必要将这种结构性变化考虑到短期利率变动中。国内现有的区制转移利率模型的实证研究中，大多采用了月度或周数据。但从固定收益债券及衍生产品的定价、风险测度等运用上看，我们更需要了解短期利率的日波动特征。因此，本文的实证研究中采用了银行间7天同业拆借市场每天的收盘利率。

本文主要采用区制转移的单因素扩散模型分析我国短期利率动态特征。首先将区制转移引入到单因素模型的漂移项和波动项部分中，可以捕捉短期利率的结构转移特征。然后，为估计利率水平和马尔科夫转移的联合动态模型，采用Aït-Sahalia的方法给出了转移密度函数近似的封闭函数表达式，并在此基础上利用汉密尔顿算法得出对数似然函数。最后，运用短期利率的四种模型对我国银行间短期拆借利率进行实证分析，考察不同数目区制约束下短期利率模型选择，考察利率波动区制转移特征，以及考察宏观经济与波动高持续性之间的内在关系。

1 短期利率模型

1.1 单因素扩散模型

本文采用的短期利率模型是CKLS单因素扩散模型

其中α0和α1是刻画利率变化条件均值参数，β为利率波动，ρ度量利率波动对利率水平的敏感度，即为弹性参数。如果ρ≠0，则波动存在水平效应。模型（1）表明利率变化具有（α0+α1rt）的漂移率和β的扩散率。可以看出短

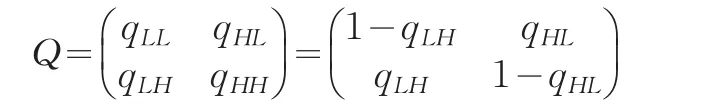
其中，密度参数qij表示，当时间趋于0并且qij＞0条件下，马尔科夫过程从状态i转移到状态j的概率速率。相应的时间间隔Δ内，转移概率矩阵为：期利率变化的条件均值和方差都依赖于利率水平。模型表明利率的长期均值为-α0/α1，并且向长期均值回归的速度由α1表示，α1值越大，均值回归速度就越快。

1.2 含区制转移的单因素扩散模型

本文在利率的CLKS随机过程基础上引入一个区制状态变量，模型变化为：

其中，区制状态变量用st表示，它服从连续时间2状态一阶马尔科夫链过程，并假设用low（L）和high（H）表示短期利率的低波动和高波动的2种不同的区制状态。那么，短期利率在任何时刻可能处在低波动区制或高波动区制。

区制转移模型使得短期利率变化的漂移项和扩散项的均是状态依赖的，其主要特点就是允许利率在不同区制状态具有不同的条件均值和方差。

1.3 马尔科夫链转移概率矩阵

驱动2状态的区制状态变量st马尔科夫链过程的转移概率密度矩阵用表示如下：

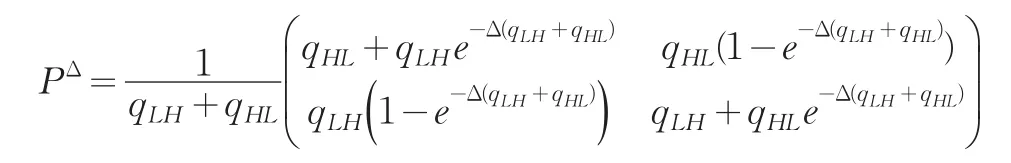
转移概率pij=P(st=j|st-1=i),i,j=L,H。马尔科夫链的稳态概率密度：

本文假设转移概率随时间变化并且参数化为以下形式：

根据经验，累计正态分布函数和Logistic函数，exp(x)/[1+exp(x)]都可以用来表示转移概率。如果di为正（负），那么在下一期随着短期利率的增大，经济停留在相同状态i下的概率增大（减少）。当dL=dH=0时，转移矩阵就退化为时间不变的转移概率矩阵。

2 极大似然估计方法

2.1 转移密度函数

本文采用Aït-Sahalia(2002)的方法将未知函数形式的真实的转移密度函数转化为近似的封闭形式的函数表达式。

在每种区制状态下，短期利率的动态行为服从模型（1）。在这一部分，将忽略区制状态st，先得到转移密度函数p(rt+Δ|rt,st)的近似封闭式函数形式，该封闭函数将用于下面一部分似然函数的构造。

首先，将短期利率rt过程用下面的等式转化为单位扩散过程Yt：

其次，采用Ito’s引理得到单位扩散过程Yt：

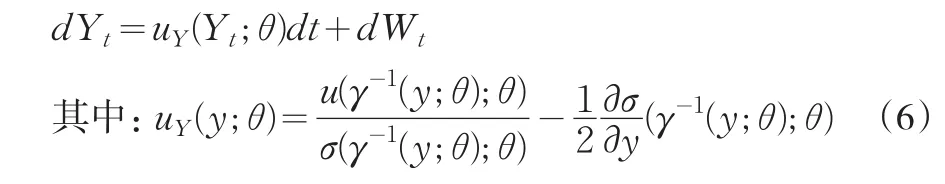
最后，将单位扩散过程Yt变换成转移密度函数近似标准正态分布的扩散过程Zt，那么就可以对pz进行Hermite扩展，如下：

其中，φ(z)为标准正态密度函数。Hermite多项式是正

条件期望可以使用无穷小操作因子AY进行泰勒展开：

因此，对于无限可导函数f，有：

利用上面的公式，py可以用下面表达式近似：

可根据时间间隔Δ的幂级数排列重新改写（8）式，得到近似密度函数PY的第K阶扩展表达式为：

实际上，大多数情况下K=1或2就能得到非常精确的密度函数。本文采用K=1，根据ρ的取值不同，可以得到不同的Yt：

根据Ito’s引理得到单位扩散过程Yt,在（10）中的任何情况都有(Yt;θ)=1，但是uY(Yt;σ)可根据（6）式的到不同的表达式。利用等式（9），转移密度函数在（10）中的任何情况下都能得到。只要得到转移密度函数，通过变量变换就可以得到r的转移密度函数：

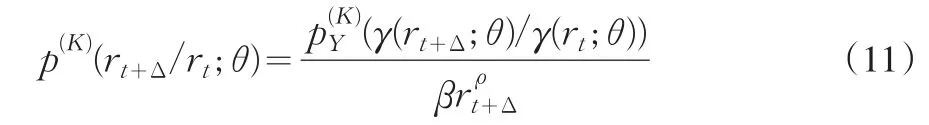
汉密尔顿算法

利用贝叶斯公式，样本的对数似然函数表达式为：

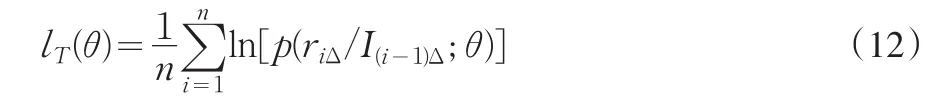
rt是在时刻{t=iΔ|i=0,1,…,n}的短期利率的观察值。首先根据（Hamilton 1994）的作法定义一个新的状态变量，如下：

那么s*t就是4状态连续时间马尔科夫链，有转移矩阵：

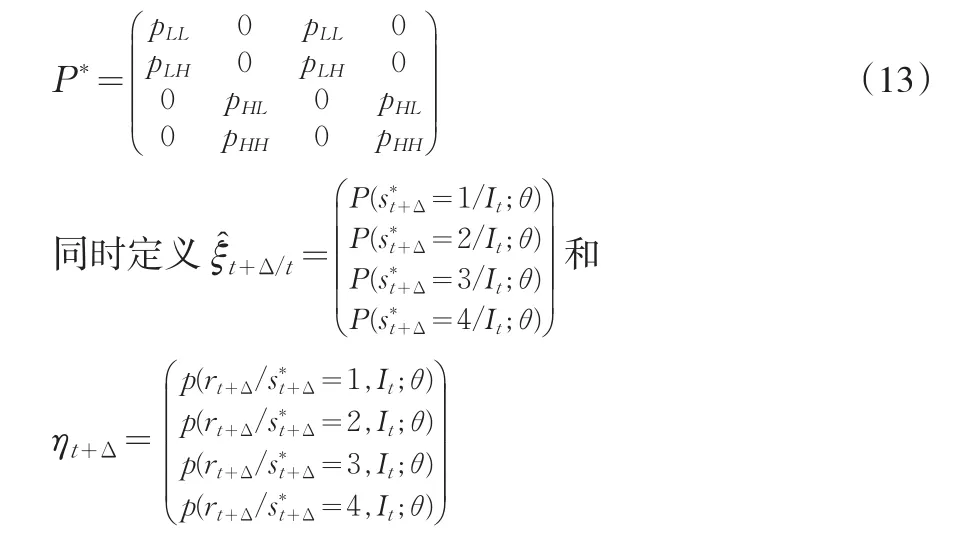
rt和的联合分布密度函数为：

2.3 平滑概率

根据极大似然估计的结果，得不到每一时刻经济将处于何种状态，本文采用平滑概率来推断在任意时刻t,经济处于高波动（H）还是低波动（L）的状态。且平滑概率为：

其中IT代表全部信息集。

3 我国短期利率的实证分析

3.1 数据来源以及估计模型

3.2 实证结果

表1给出了上诉四个模型各参数的极大似然估计值及其标准误差。从表1可以看出，模型1各参数估计值在5%水平上都很显著，其它三个模型参数估计值在5%水平下大部分是显著的。从模型2、3、4参数估计结果可以看出，两种区制下均值回归表现出显著非对称性。因为低波动区制状态下，参数α0和α1在5%水平下不显著的，因此在低波动区制时利率表现为未含趋势的随机游动过程，而在高波动区制状态利率表现均值回归行为。对于弹性参数ρ，可以发现在不同区制下均不为零，说明波动存在水平效应。

从表1可以看出，从单一区制状态模型（模型1）到具有二种区制状态模型（模型2、3、4），对数似然值显著增大。与模型1相比较，模型2、模型3和模型4的似然比统计量（LRT）分别为368.38、377.61和377.714，三个似然比统计量分别服从χ2(6)、χ2(8)和χ2(8)，0.5%的置信水平下，χ2(6)和χ2(8)的临界值分别为18.55和21.95。因此，根据似然比LR检验，拒绝只有一种区制的原假设。说明短期利率的动态行为具有二种区制。从模型2到模型3和模型4，服从χ2(2)对数似然比（LRT）统计量对应的p值分别为0.0099和0.0094。因此在1%的水平下，拒绝常数转移概率的假设，说明马尔科夫转移概率是时变的。模型3和模型4的对数似然值几乎相等，表明时变的转移概率无论是使用Logistic函数还是使用标准正态累计分布函数，对于模型的拟合效果没有影响。从表1可以看出，模型3和4中的马尔科夫转移概率的参数（c、d），dL在通常的显著性水平均显著不为零，dH在5%显著性水平下均显著为零，说明了转移概率在底波动区制状态下时时变的，而在高区制状态下是常数，并且dL＞0。因此马尔科夫转移概率随着利率水平的增大（减少），下一期停留在低波动区制状态的概率将增大（减少）。

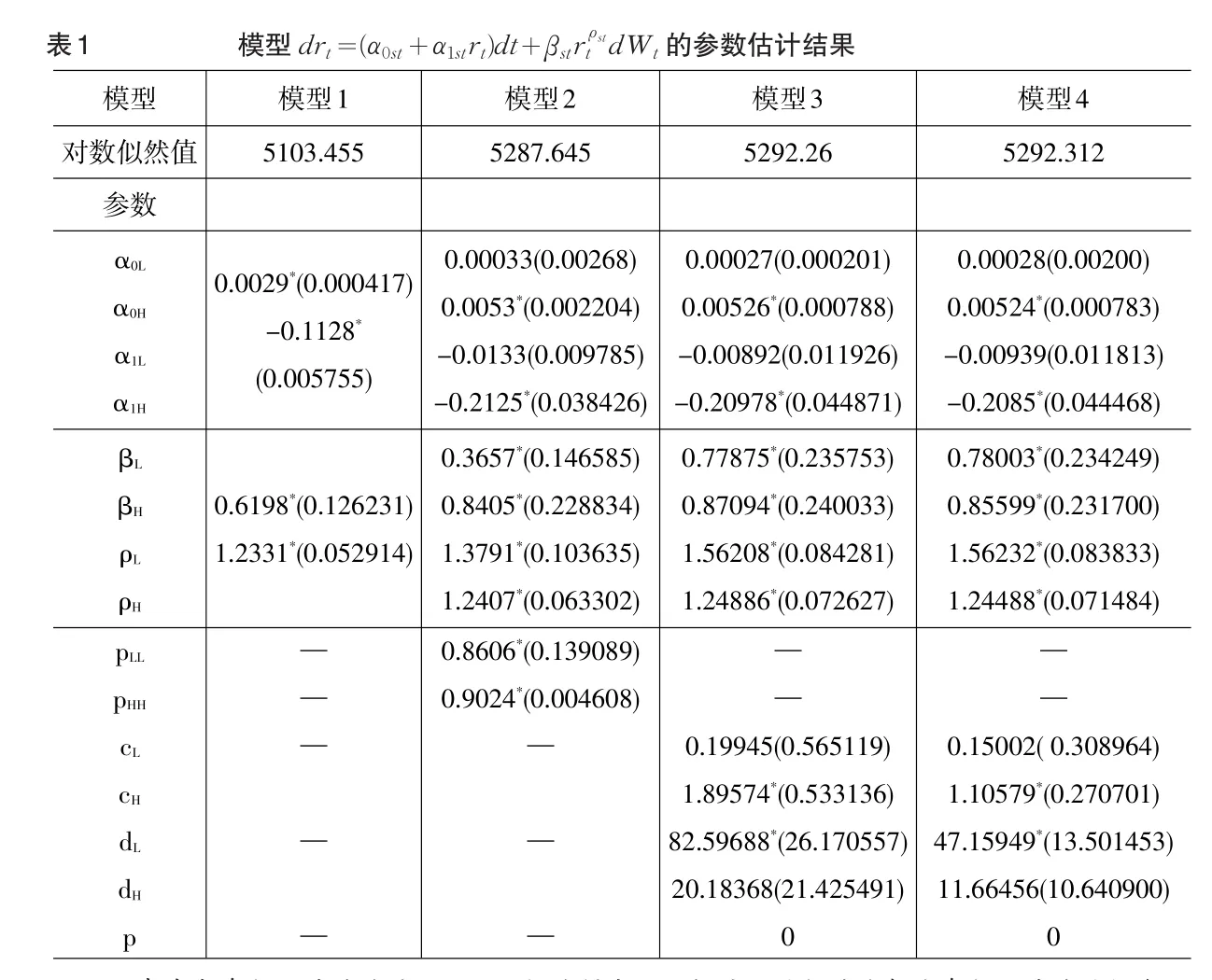
注：表中各参数估计值均是用matlab软件得出。小括号里的数值为相应参数估计值的标准误差，星号（*）表示对应参数估计值在5%水平下显著。

图1、图2和图3分别为7天同业拆借利率水平图、7天同业拆借利率差分图和模型4的高波动区制平滑概率时变图。由于模型3和模型4参数估计得到的平滑概率时变图几乎相同，这里只给出了模型4高波动区制平滑概率时变图。从图2可以看出我国银行拆借利率具有两种波动区制，高波动区制和低波动区制。如果在时刻t所观察到的区制状态i的平滑概率大于0.5，则可认为利率波动处于区制状态i。从图3可以看出，2004年第三季度，我国银行拆借利率处于高波动区制，从2004年第四季度到2005年初利率处于低波动区制，从2005年第二季度到2006年第一季度利率基本处于高波动区制，2006年下半年利率基本处于低波动区制，从2007年到2008年上半年利率又基本处于高波动区制，而2008年下半年利率又基本处于低波动区制，但是利率从2009年至观察结束日这一期间出现高低两种波动区制的频繁交替。

显然利率出现结构性动态行为与我国宏观经济状况及货币政策有关。例如2005年第二季度到2006年第一季度的利率高波动区制可能与央行灵活的公开市场操作有关,即2005年3、4月份央行票据发行规模有所增加，对冲力度进一步加大；5～8月份，央行适当调整公开市场操作力度，引导货币市场利率适度下行；9～12月份，中国人民银行适时加大公开市场操作力度，控制货币供应量增长速度，促进货币市场利率合理回升。也可能与央行分别在2005年3月17日将金融机构在中国人民银行的超额存款准备金利率下调到0.99%，7月22日、8月23日和10月15日三次上调小额外币存款利率上限的利率调控政策有关。还可能是受到国内消费需求较快增长，投资需求增速逐季加快宏观经济的影响。2007年到2008年上半年的利率高波动区制可能与2007年央行10次上调存款准备金率共5.5个百分点，2008年1月25日再次上调0.5个百分点，并6次上调金融机构人民币存贷款基准利率的“从紧”货币政策以及我国投资增长过快，价格总水平上涨较快的国内宏观经济有关。事实上，宏观经济越不稳定，货币当局越可能对经济进行调控，债券市场作出反应的可能性越大，从而未来的利率波动性越大。

而比较图1和图3可以看出，利率的高波动区制在低利率水平和高利率水平下均能发生。

4 结论

本文在单因素CKLS扩散模型基础上引入了服从连续时间2状态一阶马尔科夫链的区制状态变量，对我国银行间7日同业拆借收盘利率进行了实证研究。为实现带有区制转移变量的短期利率模型，本文采用Aït-Sahalia的方法给出了转移密度函数p(rt+Δ|rt,st)的近似的封闭函数形式表达式，并利用汉密尔顿算法得出了所要优化的对数似然函数，以及使用极大似然估计得出模型各参数的估计值。

本文的研究发现我国短期利率的波动不仅存在水平效应还存在显著的区制转换。而且在单一区制模型中引入区制转移变量后，似然比检验显示模型的拟合能力有较大的提高，因此在研究我国短期利率的波动时不容忽视结构性变化。另外，本文还发现我国短期利率在两种不同的区制状态下，其漂移项呈现非对称性，即在低波动区制时利率明显表现为未含趋势的随机游走过程，而在高波动区制则表现为均值回归过程。并且马尔科夫转移概率在高低两种不同的区制状态下也呈现非对称性，即在利率低波动区制时转移概率为时变函数，而在高波动区制时转移概率为常数。通过平滑概率分析发现，我国的宏观经济环境以及央行的货币政策与我国短期利率的结构性动态行为密切相关。因此可以通过预测国内宏观经济和货币政策方向，来推断我国短期利率在将来某一时期或某时刻处在何种区制状态的概率，这对于经济的稳定与发展，货币政策的实施及风险管理等方面有着重要指导作用。

图1 IBO007每日观察值

图2 IBO007每日利差

图3 平滑概率P（St=H|rt,…,r1）

[1]Morton,R.C.A.Dynamic General Equilibrium Model of Asset Market and Its Application to the Pricing of the Capital Structure of the Firm[C].Working Paper,MIT,1970.

[2]Vasicek Oldrich.An Equilibrium Characterization of the Tern Structure[J].Journal of Financial Economics,1977,5(20).

[3]Cox，John C.，Jonathan E. Ingersoll，Jr.，Stephen A.Ross.A Theory of the Term Structure of Interest Rates[J].Econometrica,1985，,53(2).

[4]Chan，K.C.，G.AndrewKaml，ri，FrancisA.Longstaff and An Thony B.Sanders.An Empfical Comparison of Alternative Models of the Term Structure of Interest Rates[J].The Journal of Finance,1992,47(3).

[5]Hull,J.,White,A.Numerical Procedures for Implementing Term Structure Models II:Two-Factor Models[J].The Journal of Derivatives,1994,4.

[6]Longstaff,F.A.,Schwartz,E.S.Interest Rate Volatility and the Term Structure:A Two-Factor General Equilibium Model[J].The Journal of Finance,1992,47(4).

[7]Balduzzi,P.,Das,S.R.,Foresi,S.,undaram,R.A Simple Approach to Tree-Factor Affine Term Structure Models[J].The Journal of Fixed Income,1996,6(3).

[8]谢赤，吴雄伟.基于Vasicek模型和CIR模型中的中国货币市场利率行为实证分析[J].中国管理科学,2002，(3).

[9]林海,郑振龙.中国利率期限结构:理论及应用[M].北京:中国财经出版社,2004.

[10]洪永淼,林海.中国市场利率动态研究——基于短期国债回购利率的实证分析[J].经济学(季刊),2006，(5).

[11]范龙振.短期利率模型在上交所债券市场上的实证分析[J].管理科学学报,2007,10.

[12]刘金全,郑挺国.利率期限结构的Markov区制转移模型与实证分析[J].经济研究，2006,(11).

[13]吴吉林,陶旺升.基于机制转换与随机波动的我国短期利率研究[J].中国管理科学,2009,17(3).

[14]郑挺国.基于有限混合状态空间的金融随机波动模型及应用研究[D].长春:吉林大学,2009.

[15]Aït-Sahalia,Y.Nonparametric Pricing of Interest Rate Derivative Securities[J].Econometrica,1996,64(3).