曲轴系多柔体动力学仿真分析

2011-09-04马星国尤小梅

沈阳理工大学学报 2011年6期

马星国，李想，尤小梅

(沈阳理工大学机械工程学院，辽宁沈阳110159)

曲轴是发动机的主要构件，其动力学特性对发动机的工作可靠性有较大影响。发动机周期性变化的汽缸压力和惯性力使曲轴承受较大负荷，曲轴极易发生断裂等破坏，因此有必要对曲轴进行强度、模态和疲劳寿命校核［1］。徐中明等［2］针对单缸发动机曲轴断裂问题，通过改变材料计算了最大载荷工况下的变形和应力，但在进行强度分析前没有考虑动力学特性的影响。武秀根等［3］虽然引入多体动力学方法，在ADAMS中直接进行曲轴的应力和位移等动力响应分析，但这种方法不能反映曲轴内部应力场的分布状态。吴楠等［4］采用质点力系分析方法，但难以准确地确定曲轴各轴颈载荷。

本文使用LMS公司的Virtual Lab软件，用内置的Catia v5建立V型8缸曲轴系三维实体模型，并在Virtual Lab Motion多体模块下构建曲轴系的多体动力学模型;用Nastran有限元分析软件对曲轴进行模态求解，生成op2模态文件，利用模态文件对曲轴系的真实运动和载荷进行仿真，获得曲轴五个主轴颈上的精确载荷，为研究发动机主轴承液体动力润滑提供边界条件，并为曲轴优化设计提供参考。

LMS Virtual.Lab软件是LMS公司开发的集参数化多学科多领域CAD/CAE/CAT与一体的3D仿真软件。Motion模块是基于DADS的高效稳定求解器，采用欧拉四元数法进行计算，传统算法与递归算法相结合，进行多体动力学和实验的混合计算仿真。

1 理论模型的建立

Virtual Lab Motion进行多柔体动力学分析时，一般采用Craig-Bampton模态进行求解运算，其运动微分方程以广义坐标对物体进行描述［5］，用拉格朗日法建立。

传统的C-B子结构模态综合法是将弹性结构进行有限元离散后，求解界面固定情况下的主模态;然后对界面自由度逐个施加单位位移，得到约束模态;最后用减缩主模态和约束模态组成新的模态矩阵来替代原完备模态，得到子结构的模态坐标和物理坐标的变换关系［6］为

式中:u为子结构的物理坐标;p为子结构的模态坐标;φ为模态变换矩阵，包含减缩的主模态和约束模态。

但这种方法是假设结构部件没有大范围刚体运动为前提的。而在曲轴系统中，曲轴相对于惯性系有大范围转动，属于非线性问题，必须通过正交化处理来消除子结构中刚体运动模态。将曲轴视为一个子结构，按照传统的C-B方法求得式(1)。曲轴的结构动力学方程

其中m、c、k、R分别为子结构的质量、阻尼、刚度、外力矩阵。将式(1)代入式(2)，并左乘φT，得到结构动力学方程

其中M=φTmφ，K=φTkφ，对于无阻尼自由振动可求得所需的前S阶频率和对应的正则交化模态N，即:

式中 Ns=［n1，n2…ns］。

则原来的模态坐标用修正的C-B模态坐标q来表示:

则物理坐标:

新的变换矩阵为修正的C-B模态矩阵φ与φ等价，具有原系统主模态和约束模态的所有特性，且每一个修正的C-B模态表示与频率对应。这样，零频率对应的六个刚体模态可以被显式分离出来，并可根据需要截取低段模态。

基于修正的C-B模态耦合法，由拉格动力学方程可得到柔性曲轴系的动力学方程

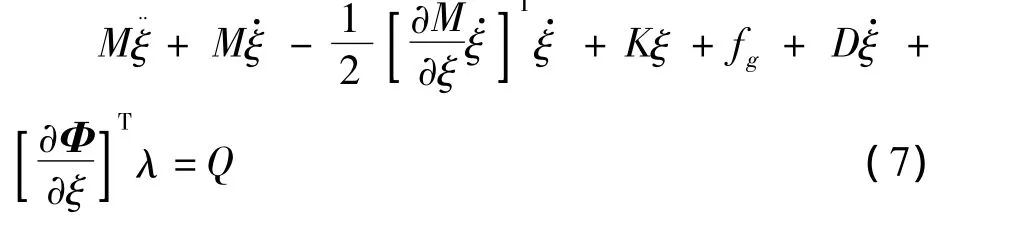
2 曲轴系动力学建模

2.1 多刚体模型的建立

Virtual.lab软件内置有Catia V5R19，其实体建模功能非常强大，可以支持在Virtual.lab里建立曲轴、连杆等部件的三维实体模型。

建立各部件的三维实体图形后进行装配。机体简化成五个轴承块，并添加相应的轴承单元，建立曲轴主轴颈轴承动力润滑模型，此方法被蔡晓霞［7］研究证明过，装配好的模型如图1所示。对于V型8缸发动机，要在8个活塞头部建立8个燃烧室单元，按照1-5-4-8-6-3-7-2的顺序设置汽缸点火顺序。

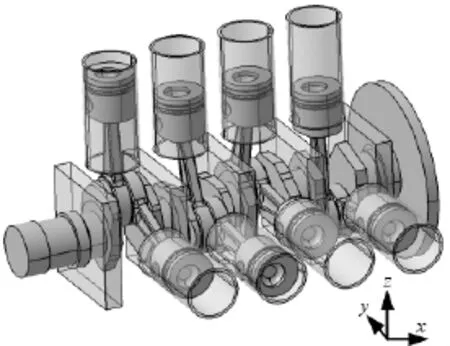
图1 曲轴系刚体模型

2.2 刚柔耦合模型的建立

2.2.1 柔性体的生成

将曲轴文件保存为step格式并导入到hypermesh中，采用hex8六面体单元划分网格，在曲轴各个运动副的部位定义rbe2或rbe3单元，曲轴有限元柔体如图2所示。设置材料参数后提交分析，从nastran模板下输出flexible body design模块计算模态所需的bdf文件。在flexible body design模块下用bdf文件替换刚性曲轴，系统根据柔性文件中定义的rbe2单元生成相应的Interface点，该点能把各运动副之间的运动和力传递到其他部件，生成Interface点，则柔性体和刚体之间建立了耦合关系。

图2 曲轴有限元模型

2.2.2 计算Craig-Bampton模态

在Virtual.lab中计算Craig-Bampton模态，需要首先设定固定界面主模态的阶数，根据模态截断准则［8］，取曲轴前12阶固定界面主模态。曲轴有17个界面连接点，约束了70个自由度，所以有70个约束模态。将12个固定界面主模态和70个约束模态进行正交化分析，去掉6个刚体模态，得到曲轴76阶的Craig-Bampton模态，前12阶模态如表1所示。

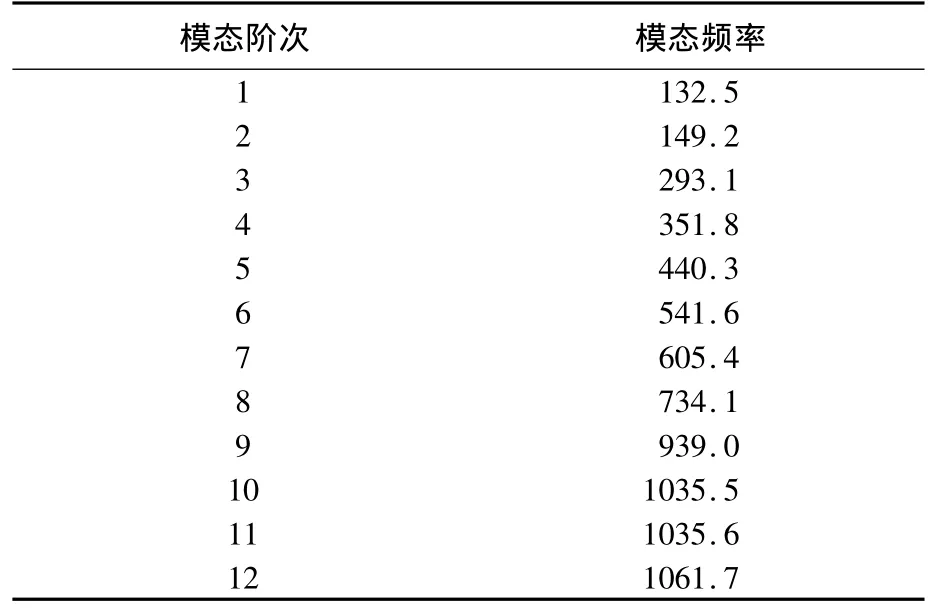
表1 柔性曲轴C-B模态频率 Hz

3 计算结果及分析

将曲轴以1000t/min转速驱动，设定仿真步长0.0002344s，仿真时间为0.24s，曲轴刚好工作两个周期。通过对计算结果分析发现，曲轴中间第三主轴颈承受较大作用力。

3.1 刚柔耦合作用下的动态载荷分析

工作周期内第三缸活塞承受的缸压作用力如图3所示。在0.18s时第三缸点火，在0.185s左右活塞承受的作用力最大。

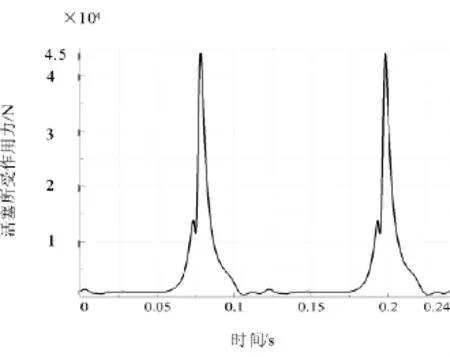
图3 缸压对活塞的作用力

曲轴在工作周期内五个主轴颈承受轴承Y向与Z向的动态反作用力如图4、图5所示(见下页)。

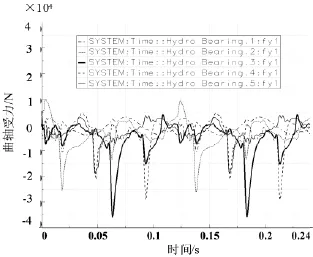
图4 轴承对曲轴主轴颈的Y向作用力

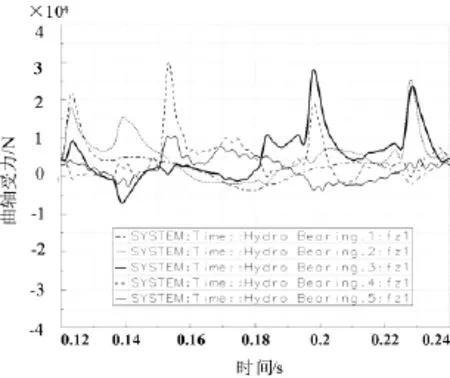
图5 轴承对曲轴主轴颈的Z向作用力

从图4、图5可以看出:曲轴五个主轴颈的受力中无论是Z向还是Y向，轴承对曲轴第三主轴颈的作用力都较大，对第一、五主轴颈的作用力较小，因为第三主轴颈处在曲轴中部位置，止推轴承安装在此处，曲轴在止推轴承的作用下不能左右串动，且左右两边的气缸点火时都会影响主轴承对主轴颈的反作用力，所以第三主轴颈承受的反作用力较大。