递推部分最小二乘方法及其应用

龚沛文，李春富，葛 铭

(杭州电子科技大学自动化学院，浙江杭州310018)

0 引言

部分最小二乘方法自Wold提出以来，作为一种基于数据回归模型的软测量建模方法，已广泛地应用于化学计量学、工业过程的建模等领域［1］。基于传统PLS出现的问题，目前出现了一系列递推算法来更加有效的更新PLS模型。该文研究了PLS回归的一种快速算法—改进的PLS核心算法，并在此基础上重新推导出递推的PLS算法，此算法提高了模型的运算速度。最后对煤气化炉合成气组分浓度的软测量建模进行了应用分析。

1 PLS核算法

PLS模型参数的计算通常采用非线性迭代部分最小二乘算法。然而对于大的数据矩阵，迭代算法效率比较低，而且NIPALS算法在迭代过程中需要存贮原始数据矩阵X和Y、残差矩阵E和F、得分矩阵T和负荷矩阵P、Q，当数据矩阵很大时将占用大量内存，且计算时很耗费时间。

针对这个问题提出来一种核算法，有效地改善了计算大数据矩阵的PLS参数问题［2］。对于“矮胖”的数据矩阵，PLS模型参数可以用协方差矩阵XXT和XTY来计算。当计算下一组参数时，只需要更新XXT和XTY。而两矩阵维数远远小于原矩阵X和Y的维数，计算速度可有较大提高。该算法的详细步骤:

(1)首先，令(XXT)1=XXT，(XTY)1=XTY，a=1。再计算协方差矩阵XXT和XTY;

(2)计算核矩阵(XTYYTX)a，这是由矩阵(XTY)a乘以其转置得到的;

(3)根据XXT和XTY计算负荷向量pa和qa

式中，向量wa代表PLS权值向量，它是对应于矩阵(XTYYTX)a最大特征值的特征向量，可以通过幂法或者其它方法计算得到;

(4)更新XXT和 XTY

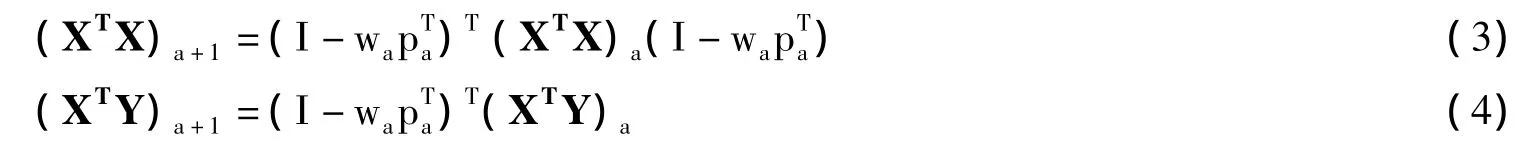
(5)令a=a+1，返回第二步，直到计算出所有需要的特征向量。

2 递推的PLS算法

该文在原始的PLS核心算法基础上，提出了一种递推的部分最小二乘算法。该算法是利用新数据和PLS模型参数组合起来更新模型，使得新模型在并不完全遗忘旧信息的基础上适应过程的新变化。

假设数据矩阵{X，Y}具有m个输入变量，p个输出变量，n个样本，采用如下形式表达对应于数据矩阵的 PLS 模型结果{T，W，P，B，Q}:

式中，假设 X 的秩为 r，T=［t1，t2，…，tr］为输入的得分矩阵，W=［w1，w2，…，wr］为输入的权值矩阵，P=［p1，p2，…，pr］和 Q=［q1，q2，…，qr］为输入和输出的负荷矩阵，B=diag{t1，t2，…，tr}为对角矩阵。

为了方便推导，将特征向量tx(x=1，2，…，r)归一化，把T标准正交。于是则有:

又矩阵Fr与T正交，由式9、10可推导出:

当加入新数据{X1，Y1}和旧数据 {X，Y}共同更新模型时，数据矩阵可写为:则有以下公式:

同理可得:

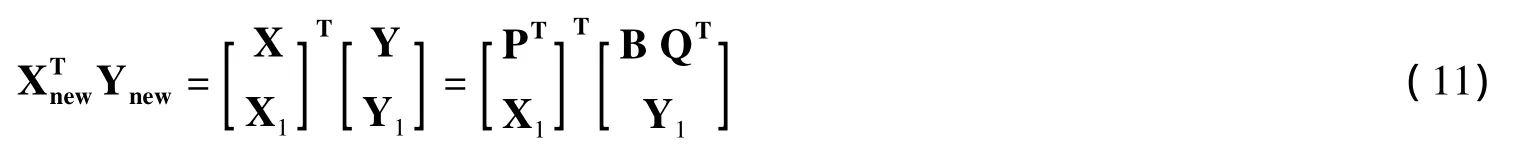
因此，由式10、11可以得知，对现有全部数据的回归等价于对新数据结合老数据而得到的PLS模型参数回归。由此很容易推导出RPLS算法，步骤如下:

(1)确定过程变量，选择模型参数;

(2)采集数据，构造原始数据矩阵{X，Y}，并对其进行数据预处理;

(3)采用PLS的核心算法计算出PLS模型{X，Y}—PL→S{T，W，P，B，Q};

(4)加入新数据后，根据步骤1进行数据预处理，然后利用遗忘因子法对旧参数矩阵进行加权，即用遗忘因子可用遗忘因子λ(0＜λ≤1)与旧参数矩阵相乘从而达到削弱旧数据对建模的影响的作用，再和旧参数组成新数据矩阵，最后返回步骤3。

3 RPLS算法在软测量建模中的应用

该文以煤气化炉装置为建模对象，根据现场工艺以及反应机理的分析，一共选择11个过程变量作为模型的输入变量，合成气组分CO作为模型的输出变量。首先取43个初始数据集合建立PLS模型，同时为了在更新模型时不丢失原数据的信息，在建立PLS模型时需要保留的特征向量数目要足够多，可根据对响应变量的解释程度来确定。当新增加的特征向量对响应变量的解释程度小于某个阈值，或者新增一个特征向量之后，对响应变量总的解释程度大于某个阈值，比如90%，则停止增加特征向量，利用已经提取的特征向量进行预测。

然后取第44到第64的数据为第二组数据，预测结果如图1所示，虚线为实际值，实线为模型预测值。仿真表明预测结果误差较大，尤其是第58个数据点的值突然变大，因此，模型需要及时更新。该文采用递推的PLS算法来对模型进行更新。在新数据到来后，和旧模型参数矩阵进行PLS回归，得到更新后的模型再对第二组数据进行预测，结果如图2所示。两种不同模型的性能比较如表1所示。可以看出，模型更新后的预测均方根误差有较大减小，模型的预测精度有了很大的提高。

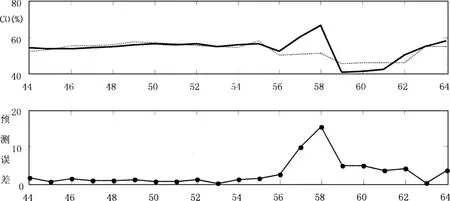
图1 模型对第二组数据的预测结果

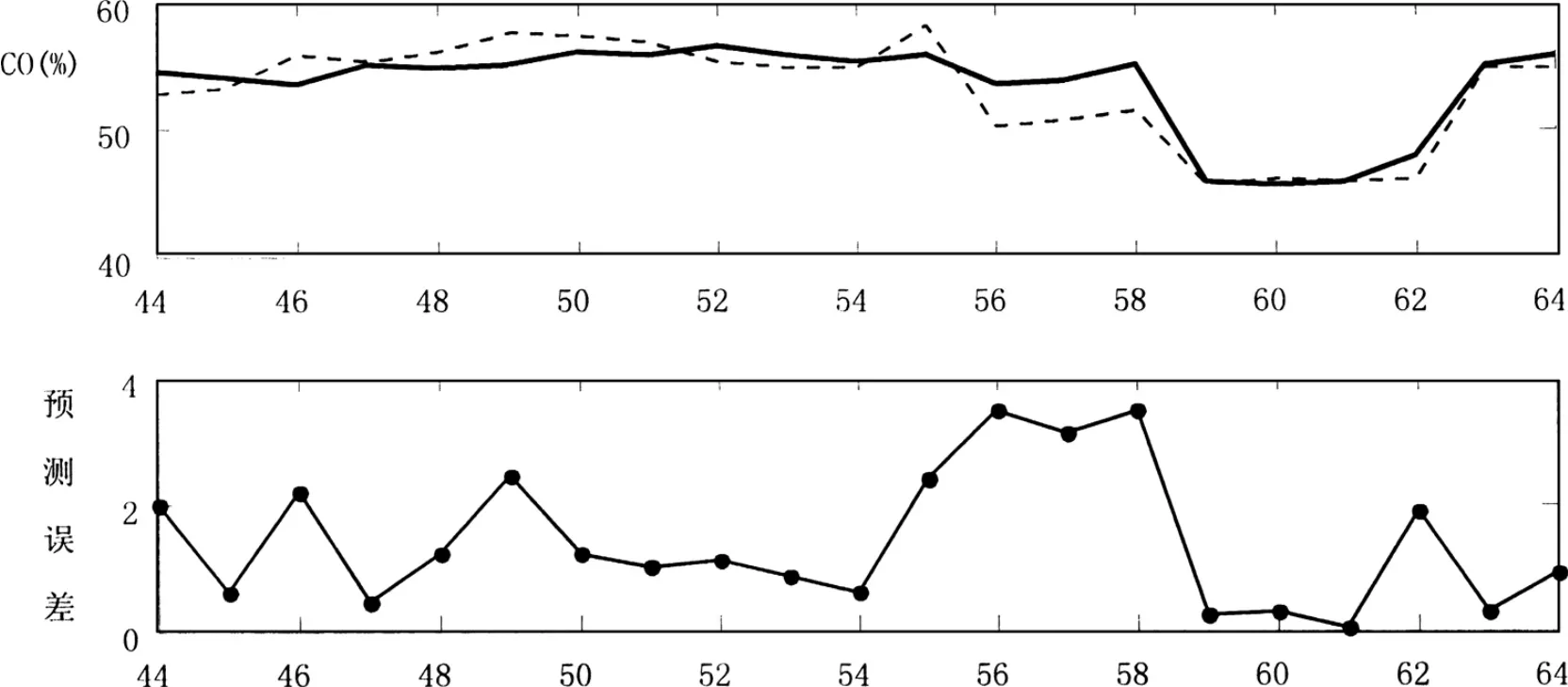
图2 更新后的模型对第二组数据的预测结果

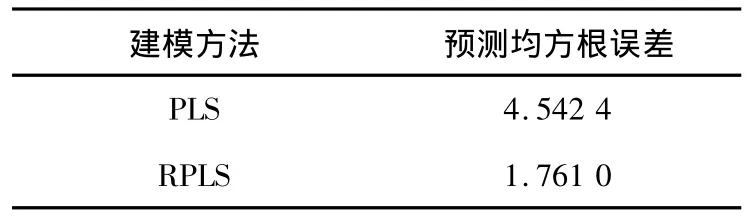
表1 两种模型的性能比较

4 结束语

该文以一种新的推导方式，提出了递推的部分最小二乘算法。该算法可以根据新的数据和旧的PLS模型参数更新模型，而不需采用全部数据。仿真结果表明该算法可以有效的更新模型，使模型适应过程的变化。然而，在建立模型时所确定的特征向量个数不一定是最优的。因此，在线更新模型时，如何确定用于预测的最优特征向量数，还有待进一步研究。

［1］ Wold H.Nonlinear estimation by iterative least squares procedures［J］.Research Papers in Statistics，1966，12(5):134－139.

［2］ Lindgren F，Geladi P，Wold S.The kernel algorithm for PLS［J］.Chemometrics，1993，7(22):45 －59.

［3］ 张杰，阳宪惠.多变量统计过程控制［M］.北京:化学工业出版社，2000:2－67.

［4］ 李凡，吴强，杨英华，等.基于递推PLS的自适应钢温软测量模型［J］.控制工程，2007，8(2):147－150.

［5］ Helland I S.On the structure of partial least squares regression［J］.Comm.Statist.B-Simulation Compute，1988，17(3):581－607.

［6］ Lakshminarayanan S，Shah S L，Nandakumar K.Modeling and control of multivariable processes:dynamic PLS approach［J］.AIChE Journal，1997，43(9):2 307 －2 322.