基于Fourier-Mellin变换的红外图像配准

高炳像，刘 俊

(杭州电子科技大学信息与控制研究所，浙江杭州310018)

0 引言

目前国内外对图像配准的研究主要集中在3个方面:特征空间、搜索策略、相似性度量。根据这3个基本要素选择的不同，图像配准的方法分为3个大类:基于图像灰度信息的方法，如模板匹配法［1］;基于变换域的方法，如基于傅里叶变换的方法［2］;基于图像特征的方法，如边缘、角点方法［3］。本文算法基于相位相关法［4］提出，只要配准的两幅图像中具有一个相同信息的小区域，该算法就可以实现配准。

1 基于Fourier-Mellin变换的图像配准原理

1.1 傅里叶变换的平移特性

如果图像f2(x，y)是图像 f1(x，y)经平移(x0，y0)后的图像，即:

对应的傅里叶变换F1和F2的关系为:

且对应频域中两个图像的互能量谱为:

通过对互能量谱进行傅里叶反变换，就可以得到一个单位脉冲函数δ(x－x0，y－y0)，该函数在偏移位置有明显的尖锐峰值，据此特性就能找到两图像的相对平移量x0和y0。对式3进行傅里叶反变换产生一系列脉冲峰值，其中最大峰值对应的位置就是相对平移量。

1.2 基于Fourier-Mellin变换的配准方法

假设两幅需要配准的图像为s(x，y)和r(x，y)，其中s(x，y)是r(x，y)经过平移、旋转和一致尺度缩放(即两个方向上的尺度变换因子相等)变换后的图像，即:

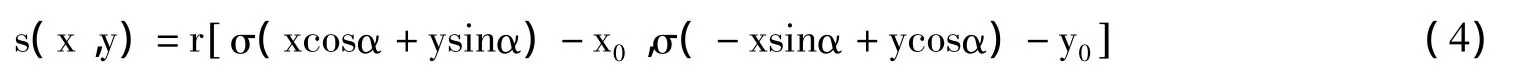
对应的傅里叶变换S(u，v)和R(u，v)之间满足:

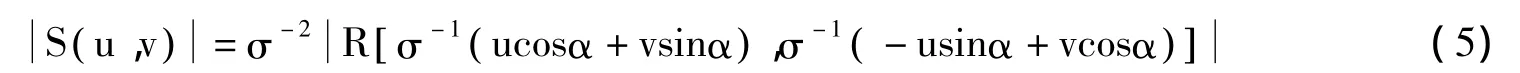
式中，|·|表示频谱幅度，仅与旋转角度α和缩放因子σ有关，而与平移量x0和y0无关，因此，相似变换的参数可以分两步求得。

(1)利用相位相关法估计旋转角度和缩放因子［5］:

式中，rp和 sp分别是图像r(x，y)和s(x，y)在极坐标系(θ，ρ)中的幅度谱，容易得出:

令 λ =logρ，μ =logσ，式8转化为:

式9称为Fourier-Mellin变换，按照前面提到的相位相关法可以求得α、μ以及σ。

(2)利用相位相关法估计平移参数［6］

根据求得的α和σ，对原图像进行缩放和旋转校正，再利用相位相关技术求得平移量。

2 实验结果

根据所提出的图像配准算法，用MATLAB进行仿真实验，实验结果如下:如图1所示利用相位相关法估计平移参数，图1(a)为原图像，图1(b)为图1(a)平移(25，25)后得到的图像，图1(c)为两图像的互能量谱图，图1(d)为该互能量谱傅里叶反变换的三维显示图，从图1(d)可看出存在明显的峰值，正好对应于坐标(25，25)处，所以利用相位相关法可以比较精确地算出平移参数。

图1 利用相位相关法估计平移参数

如图2所示利用相位相关法估计旋转角度和缩放因子，图2(a)为原图像，图2(b)为图2(a)旋转15°后得到的图像，图2(c)和图2(d)分别为图2(a)和图2(b)的对数极坐标图像，图2(e)为两对数极坐标图像的互能量谱图，图2(f)是该互能量谱傅里叶反变换的三维显示图，由图2(f)可看出存在明显的峰值，正好对应于坐标(15，0)处，由此可得旋转角度α=15°，缩放因子σ=eμ=e0=1，即利用相位相关法也可以比较准确地计算出旋转角度以及缩放因子。

对于同时存在平移和旋转变换的配准情况:例如以图2(a)为参考图像，以先平移(25，25)，再旋转15°的图像作为待配准图像进行配准。配准的结果如表1所示。

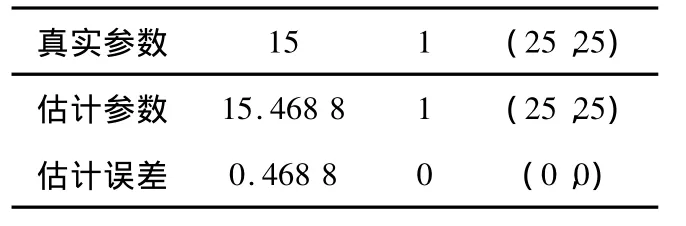
表1 配准参数的估计比较

从表1中可以看出，该算法能够得到比较精确的配准参数。

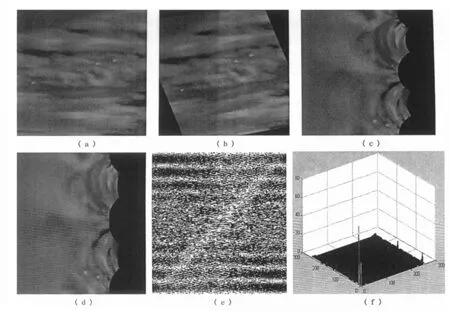
图2 利用相位相关法估计旋转角度和缩放因子

3 结束语

本文首先分析了只存在平移变换的图像配准;然后讨论了同时存在平移和旋转变换的配准问题。通过MATLAB实验可知，只有两幅图像的中心点重合时，它们的对数极坐标图像的互功率谱经过傅里叶反变换后才能够产生二维的脉冲信号，本文中需要进行配准的两幅图像具有一个相同信息的小区域，相应的对数极坐标图像的互功率谱经过傅里叶反变换后可以产生二维脉冲信号，从而能够比较准确地估计出配准参数，实验结果说明了该算法的有效性和可实现性。

［1］ 高军，李学伟，张建，卢秉恒.基于模板匹配的图像配准算法［J］.西安交通大学学报，2007，41(3):307－311.

［2］ 强赞霞，彭嘉雄，王洪群.基于傅里叶变换的遥感图像配准算法［J］.红外与激光工程，2004，33(4):385－388.

［3］ 杨柳青.基于角点和边缘特征的图像配准方法的研究［D］.南京:南京理工大学，2009.

［4］ 郑志彬，叶中付.基于相位相关的图像配准算法［J］.数据采集与处理，2006，21(4):444－449.

［5］ 许东，安锦文.基于图像对数极坐标变换的多分辨率相关匹配算法［J］.西北工业大学学报，2004，22(5):653－656.

［6］ 马金福，薛弘晔.基于Fourier-Mellin变换的图像配准算法及性能研究［J］.计算机与数字工程，2008，36(11):134－136.

［7］ Kuglin C D，Hines D C.The phase correlation image alignment method［C］.New York:IEEE International Conference on Cybernetics and Society，1975:163 －165.