褶皱正交剖面的计算机辅助编绘

刘国生， 刘焕玉， 刘亚东， 黄 磊， 翁新镇， 宋彦臣

（1.合肥工业大学 资源与环境工程学院，安徽 合肥 230009；2.山东省城乡建设勘查院，山东 济南 250031）

褶皱是构造地质学研究的重要对象，只有清楚地认识了褶皱的几何形态特征、空间变化及分布规律，才有可能进行物理模拟或数学模拟，研究它们的形成机制。

褶皱几何学是构造地质学中一个古典的研究领域，在文献［1］对包括褶皱在内的构造的几何学研究方法进行了综述［1］。随着学科的发展，对褶皱的几何学研究也在不断深入，研究褶皱构造的新理论和新方法不断出现，如文献［2］提出了基于二次Bézier曲线的褶皱形态分析，文献［3］使用MATLAB程序对褶皱进行形状分类，文献［4］对褶皱几何学研究中的一些进展进行了概括和总结。这些研究成果多数是基于平面上的分析，而褶皱正交剖面正是褶皱构造解析的基础，但由于多方面的因素，在对自然褶皱的研究中，正交剖面的应用并不广泛。

本文选择有着一定研究程度的巢湖北部山区［5］，以巢湖市北部山区平顶山向斜为例，对褶皱正交剖面的绘图方法进行了讨论，概括了编绘褶皱正交剖面的一般程序，提出了应用计算机辅助作图的方法，以期达到将新理论应用到实际中的目的。

1 褶皱正交剖面的制图原理

褶皱的几何形态可以由它的平面图和剖面图反应出来，研究褶皱的文章一般都附有铅直或横剖面图（cross section），这种剖面表示的构造一般是在垂直于褶皱枢纽总体走向上选取的铅直剖面中的外貌。在褶皱变形较为简单和枢纽较平缓的地区，铅直剖面能够很好地表现构造，但在褶皱枢纽非近水平、特别是枢纽高角度倾伏的复杂褶皱地区，绘制铅直剖面，则不能够正确、全面认识褶皱构造形态，甚至会形成错误印象［6］，这时正交剖面就显示出它的优势。正交剖面是与褶皱枢纽相垂直的剖面，它能够表示出褶皱的真实形态，包括正确的翼间角、褶皱层曲率以及褶皱岩层厚度的变化等。

编绘褶皱正交剖面的前提是褶皱可以视为圆柱状或次圆柱状，自然界中的褶皱一般较为复杂，很少有严格意义上的圆柱状褶皱，通过实践，可以将褶皱划分为若干个区段，在每一区段内，褶皱可以视为圆柱状的。

圆柱状褶皱在水平面、铅直剖面和正交剖面上存在着一定的空间关系，如图1所示。

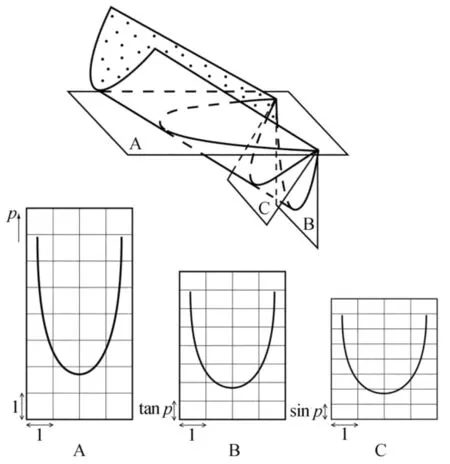
图1 褶皱平面与剖面之间的空间关系

图1中A为平面图，B是铅直剖面，C为正交剖面，p为枢纽倾伏角。当褶皱倾伏，枢纽倾伏角为p时，平面图上1∶1的网格转换到铅直剖面上变为1∶tan p，转换到正交剖面上则变为1∶sin p。褶皱正交剖面的作图正是应用了水平面与正交剖面之间的几何关系，即将水平地质图沿枢纽倾伏方向按sin p的比例压缩。特殊地，当枢纽水平时，正交剖面相当于铅直剖面；当枢纽直立时，正交剖面与水平面相同。

曾有学者提出，可以通过褶皱的铅直剖面得出正交剖面［7］，笔者认为，在缺少钻孔资料的条件下，这样得出的正交剖面并不精确。平面图与铅直剖面图都需要投绘产状数据，平面图投绘的是岩层的走向，圆柱状褶皱中，在沿走向上产状变化最小；而铅直剖面投绘的是岩层的倾角，是圆柱状褶皱产状变化最大的方向，因此，由平面地质图作出的正交剖面更为精确。

2 计算机辅助编绘正交剖面的方法

传统上较为常用的编绘褶皱正交剖面的方法是利用方格网来手绘。这种方法只介绍了如何将一段枢纽产状已知的褶皱平面图绘制为正交剖面图，但并未对从野外地质调查到绘制正交剖面的全过程进行总结，而且手绘较麻烦，编绘的准确程度受人为因素的影响也较大。

笔者通过对编绘巢湖北部山区褶皱正交剖面的大量尝试，概括出一套利用计算机辅助编绘正交剖面的一般程序。

（1）野外数据采集与地质填图。野外工作人员经过踏勘，要对褶皱的形态有一个正确的认识，并且尽可能多地测量褶皱层的产状数据。另外，地质图要求绘制准确，因为这是编绘正交剖面图的基础。

（2）利用计算机将地质图矢量化。笔者使用的矢量化绘图软件为Adobe illustrator。

（3）在野外实地调查的基础上，根据褶皱枢纽产状的变化，将褶皱划分为若干个区段，在每个区段内褶皱可视为圆柱状或次圆柱状。

（4）将褶皱层的产状在吴氏网上进行投绘（可使用相关软件），得到层面极点图，绘出π圆，然后观察是否有90%以上的点落入π圆两侧10°或20°范围内，若落在10°范围内为圆柱状褶皱，若落入20°范围内则为次圆柱状褶皱。

这里需要强调一下，为了保证投影的准确，投绘的产状应该来源于褶皱两翼对应层位。

（5）读出吴氏网中β轴产状，即可视为褶皱枢纽的产状。

（6）在矢量图中将本区段褶皱面的轮廓选中，并逆时针旋转，旋转的角度等于枢纽倾伏向的度数，此时得到一幅沿倾伏方向观察的褶皱地质图。

（7）将旋转后的地质图在纵向（即倾伏方向）上压缩，压缩的比例等于枢纽倾伏角的正弦值，横向上比例不变。

经过如上操作，就绘出了一幅沿褶皱倾伏方向下视的正交剖面图。上述方法是以地形平坦为前提的，如果地形起伏较大时，应根据地形等高线进行校正，具体步骤可参见文献［1］。另外，在枢纽倾伏向不变，倾伏角逐渐变化的地区，可以分区段制图之后，将各区段的正交剖面连接起来构成一幅整体上的近似的正交剖面图。

3 褶皱正交剖面计算机辅助编绘实例

3.1 巢湖平顶山向斜石炭系褶皱层正交剖面

下面以巢湖北部山区平顶山向斜石炭系（C）转折端为例，对上述方法进行应用。

平顶山向斜石炭系（C）转折端出露于巢北向核山，地势高差较小，地形基本平坦，转折端较为清晰。

通过野外调查绘制了本段的地质图，如图2所示，并将野外测得的产状投绘为层面极点图，如图3所示，其中n为极点数。由图3可见层面极点有90%以上都处于π圆两侧10°范围内，因此本段可视为圆柱状褶皱，读出β轴产状为218°∠20°。

图2 巢湖北部山区平顶山向斜石炭系转折端地质图

在Adobe illustrator中，将本段石炭系（C）的轮廓线选中，逆时针旋转218°，然后纵向上按sin 20°＝0.34的比例进行压缩，即可得到本段沿倾伏方向下视的褶皱正交剖面，如图4所示。

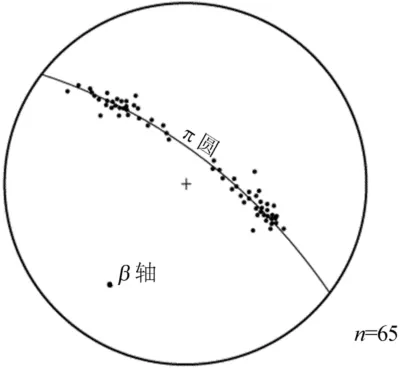
图3 平顶山向斜石炭系转折端层面极点等密图

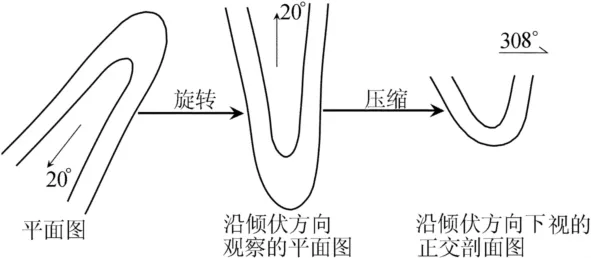
图4 计算机编绘平顶山向斜石炭系转折端正交剖面过程

3.2 与手工绘制的正交剖面比较

在前期对研究区平顶山向斜的研究中，采用传统上的手工绘图方法，得到平顶山向斜石炭系褶皱层的正交剖面，如图5所示，获得石炭系（C）褶皱层的等倾斜线均向内弧收敛，内弧曲率大于外弧曲率，属于Ramsay分类中的Ⅰ类褶皱。对比本文由计算机辅助编绘出的平顶山向斜石炭系褶皱层正交剖面（图4），两者吻合一致，反映出该方法是可行的。

图5 平顶山向斜正交剖面的手工绘图（逆枢纽倾伏方向）

4 正交剖面在褶皱研究中的作用和意义

褶皱的几何研究一般在轮廓平面上，通过褶皱层厚度的变化进行分析［4］。得到褶皱的正交剖面之后，即可对褶皱层进行几何分析，最基本的就是作等倾斜线，进行 Ramsay分类［6，8］。Ramsay分类是对单个褶皱进行几何学分析的一个优秀工具，并且是在特定情况下研究褶皱机械运动所必不可少的［4］。文献［3，9－10］分别对 Ramsay分类进行了改进和细化，文献［11］还将Ramsay分类方法延伸到多层的褶皱层的分类上。在Ramsay分类的基础上，还可以做出tα′曲线，tα′曲线在一定程度上反映了褶皱的应变特征。

文献［12］建议用立体Bézier曲度来匹配和分级褶皱面轮廓；文献［13］则通过在一个平面上以不同角来切割一个圆锥体所得到的曲线来描述褶皱；文献［14］提出了对于压扁平行褶皱的一种快速应变估计方法；文献［15］提出了同心褶皱的应变测定方法；文献［16］提出从褶皱形状估计应变和能干性对比等等。上述成果，都是在垂直于褶皱枢纽方向的剖面上进行的，可见褶皱正交剖面在褶皱几何学分析中是十分重要的。

5 结束语

褶皱几何学研究是褶皱运动学研究的基础，而正交剖面在褶皱几何学中又有着重要的地位和作用。本文对从野外地质调查到绘制正交剖面的程序进行了概括，提出了利用计算机辅助编绘褶皱正交剖面的方法，并以巢湖北部山区褶皱——平顶山向斜为例进行了分析，其结果与手工绘制的正交剖面进行了比较，结果吻合。实践检验表明，该法在保证精度的前提下提高了效率，该方法对将褶皱几何学研究的新成果应用于实际中有一定的促进作用。

［1］Ragan D M.构造地质学：几何方法导论［M］.邓海泉，译.北京：地质出版社，1984：82－91.

［2］Liu C，Zhang Y，Wang Y.Analysis of complete fold shape based on quadratic Bézier curves［J］.Journal of Structural Geology，2009，31：575－581.

［3］Lisle R J，Fernández Martínez J L，Bobillo－Ares N，et al.FOLD PROFILER：a MATLAB－based program for fold shape classification［J］.Computers ＆ Geosciences，2006，32：102－108.

［4］Bastida F，Aller J，Bobillo－Ares N C，et al.Fold geometry：a basis for their kinematical analysis［J］.Earth－Science Reviews，2005，70：129－164.

［5］宋传中，牛漫兰.巢湖北部青苔山推覆构造的特征及其成因［J］.合肥工业大学学报：自然科学版，1999，22（6）：15－19.

［6］Ramsay J G，Huber M I.现代构造地质学方法，第2卷：褶皱和断裂［M］.徐树桐，陈冠宝，江来利，等，译.北京：地质出版社，1991：41－77.

［7］王颂禹.地质构造形态定量研究初探［J］.同济大学学报：自然科学版，1988，16（1）：65－72.

［8］Ramsay J G.岩石的褶皱作用和断裂作用［M］.单文琅，宋鸿林，蒋荫昌，译.北京：地质出版社，1985：244－254.

［9］Hudleston P J.Fold morphology and some geometrical implications of theories of fold development［J］.Tectonophysics，1973，16：1－46.

［10］Zagorcev I.The geometrical classification of folds and distribution of fold types in natural rocks［J］.Journal of Structural Geology，1993，15：243－251.

［11］Srivastava V，Gairola V K.Geometrical classification of multilayered folds ［J］.Tectonophysics，1999，301：159－171.

［12］Srivastava D C，Lisle R J.Rapid analysis of fold shape using Bézier curves［J］.Journal of Structural Geology，2004，26：1553－1559.

［13］Aller J，Bastida F，Toimil N C，et al.The use of conic sections for the geometrical analysis of folded surface profiles［J］.Tectonophysics，2004，379：239－254.

［14］Srivastava D C，Shah J.A rapid method for strain estimation from flattened parallel folds［J］.Journal of Structural Geology，2006，28：1－8.

［15］Srivastava H B.Strain determination from concentric folds［J］.Tectonophysics，2003，364：237－241.

［16］Schmalholz S M，Podladchikov Y Y.Strain and competence contrast estimation from fold shape［J］.Tectonophysics，2001，340：195－213.