基于遗传算法的汽车变速箱轻量化设计

褚永康， 文桂林， 崔 中， 文 登

（湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082）

0 引 言

当今汽车技术的发展由于受到环境、资源等问题制约，轻量化的汽车在燃油经济性、排放物等级方面都具有更强的市场竞争力，因此，汽车轻量化技术成为十分必要的研发课题。目前，对于现有车型的轻量化，主要方法是从零部件轻量化做起，逐步积累，最终达到整车轻量化的目标［1］。汽车的轻量化最终要分解落实到相关零部件的轻量化，本文的研究也是基于零部件的轻量化进行的。

随着计算机技术的发展，CAE技术已经广泛应用于汽车零部件轻量化的研究中［2－3］。然而这种方法虽然借助了CAE技术，但是模型的修改仍然按照经验进行，再进行有限元仿真计算验证，如不满意再更改几何模型，循环进行直到找到满意结果。这样不仅带有很大的盲目性和随机性，而且需要大量的仿真导致效率低、耗时长。

本文的研究以满足力学、振动等特性为切入点，结合有限元方法，将数值优化算法等现代设计方法引入轻量化设计过程中，以克服优化的盲目性。以某型电动大巴变速箱箱体为例，在有限元分析的基础上，对建立的径向基函数近似模型用遗传算法进行寻优设计，成功地对其箱体结构进行轻量化设计，取得了良好的效果。

1 变速箱有限元分析

1.1 变速箱箱体有限元模型建立

（1）三维模型建立。在UG三维建模软件中建立某型电动大巴变速箱三维模型。为了方便对其进行有限元分析，需要对有限元分析影响不大的箱体结构进行简化，简化的原则如下：在不改变箱体模型特性的基础上，简化倒角、圆角、小孔、螺纹等特征，以免计算有限元模型时造成太大的计算量。最终模型简化结果如图1所示。

图1 变速箱箱体三维模型

（2）网格化分。将UG得到的模型转化为parasolid格式后导入MSC.PATRAN软件中，对变速箱箱体进行整体划分，考虑到砂轮架的内部结构比较复杂，为了提高有限元计算的精度，故采用高阶四面体单元对砂轮架进行网格划分，单元长度为20mm。变速箱箱体模型共有33 351个节点，16 939个单元。

（3）边界条件及材料参数。箱体底部有4个螺栓安装孔，PATRAN中采用MPC约束的方法来模拟螺栓安装，并按照箱体在轴承孔处的受力建立场力。箱体材料为HT200的铸铁材料，从手册中查得 E＝120kPa，μ＝0.25，ρ＝7.2×10－9t／mm3。有限元模型如图2所示。

图2 变速箱箱体有限元模型

1.2 变速箱静力学分析

在MSC.NASTRAN软件中对模型进行静力学分析，分析结果如图3所示，最大应力出现在箱体底部螺栓孔处，应力值的大小为64.6MPa，远小于材料的许用应力200MPa，其他部位所受应力较为均匀；最大位移量出现在箱体顶部，位移为0.055 6mm。

图3 变速箱静力分布结果

1.3 变速箱模态分析

考虑到整个动力总成的工作频带，变速箱的前几阶模态有着重要的作用，尤其是第1阶固有频率。由于篇幅原因只列出前4阶模态，箱体约束条件下模态分析结果见表1所列。

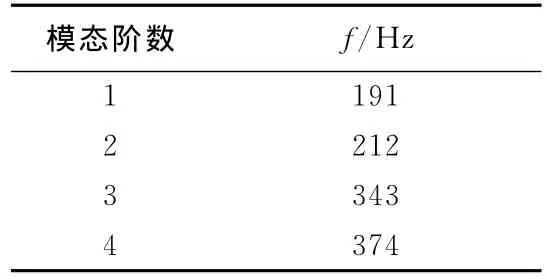
表1 箱体前4阶模态

前4阶模态阵型变形图如图4所示。

通过以上模态阵型图可以看出，第1阶与第2阶阵型主要表现整体的扭转振动，第3阶与第4阶阵型主要表现为四壁及上下板局部的弯曲和扭转。振动的第1阶频率191Hz远高于系统发生共振的频率120Hz。以上强度、静刚度及模态分析结果与设计允许值之间存在较大的余量，故为箱体进行轻量化设计提供了依据。

图4 变速箱箱体前4阶阵型图

2 变速箱轻量化设计

由于利用有限元模型进行计算的时间周期会较长，调用其模型进行优化，计算效率会大大降低。如果采取近似模型代替有限元模型，则可以相应地提高计算效率。本文先采用拉丁超立方试验设计方法建立了模型样本点，然后基于径向基函数建立近似模型，最后利用遗传算法优化程序对箱体的质量进行优化，从而达到对其结构轻量化的目的。

本文优化设计目标函数为箱体的质量，在影响质量的诸多因素中，对壁厚的优化是最为可行的，因此选取箱体底面壁厚k1、轴向壁厚k2及侧向壁厚k3为此次优化的设计变量。优化问题可描述如下：

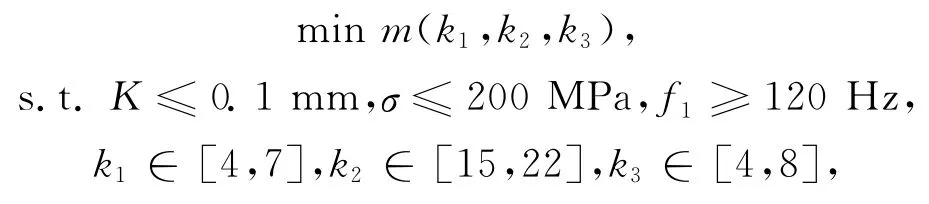
其中，m为箱体质量；K为箱体静刚度；σ为箱体强度值；f1为第1阶振动频率，其值的确定范围根据设计要求确定。上述k的取值范围是根据箱体设计规格和加工要求确定的，单位均为mm。其具体优化流程如图5所示。

图5 优化流程图

2.1 试验设计方法

基于回归分析的近似模型方法是针对样本数据进行操作的，因此样本点选取的优劣决定了所构建的近似模型的正确性。为建立精度和效率都较高的近似模型，需要选取合适的样本点，如果样本选择不当则有可能造成近似模型精度较低，甚至错误等结果［4］。本文采用优化拉丁超立方试验设计方法，该方法的基本思想是将每个设计参数的设计空间均匀地划分为边长为N的方阵，然后在方阵中随机取得不同行不同列的N个采样点。此方法的采样点比较均匀，可获得充分的模型信息。

采用优化拉丁超立方试验设计方法，获取30组样本点，即得到30组壁厚尺寸参数，由于篇幅原因仅列出一些样本，数据见表2所列。

表2 箱体壁厚参数样本点

根据30组样本点，分别建立30个箱体的集合模型，计算出各自的质量，进而分别建立有限元模型，进行静力学分析和模态分析，得到每组最大应力值、最大变形量及第1阶固有频率的结果。

2.2 径向基函数近似模型

近似模型的基本思想是，通过数理统计和试验设计的方法，在设计变量和相应值之间建立一种现实的函数关系来近似复杂的实际问题或函数。常用的近似模型方法有Kriging响应面法、径向基函数法、多项式响应面法及移动最小二乘法等，径向基函数近似模型在考虑精度和鲁棒性时相对于其他近似模型是相对可靠的［5－6］，故本文采用径向基函数来建立变速箱箱体的近似模型。

径向基函数模型是一种基于样本点构造的插值近似方法，可以无偏差量地通过每一个样本点。由于高斯函数具有在输入数据和训练样本差异较大时仍能可靠地插值高维空间中数据集的优点［7］，故本文选用高斯函数为径向基函数，径向基函数模型的表达式如下：

其中，D为权系数；L为待测点到样本点的欧式距离；A为给定的大于零的常数［8］。经过反复计算，可以确定对于质量的径向基函数F1（L）的权系数，定A1＝0.9，权系数D1取值如下时，径向基模型与采样点拟合最好。

对于强度的径向基函数F2（L）的权系数，定A2＝0.9，权系数D2取值如下时，径向基模型与采样点拟合最好。

对于静刚度的径向基函数F3（L）的权系数，定A3＝0.3，权系数D3取值如下时，径向基模型与采样点拟合最好。

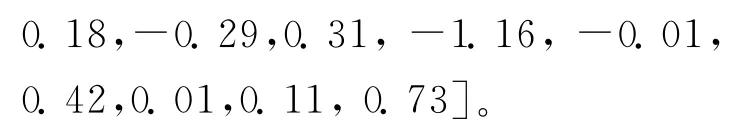
对于第1阶模态的径向基函数F4（L）的权系数，定A4＝0.8，权系数D4取值如下时，径向基模型与采样点拟合最好。

2.3 基于遗传算法的轻量化设计

遗传算法是模拟自然界中生物的遗传和变异过程而形成的一种自适应全局优化概率搜索算法。目前，在遗传算法的基础上发展了一些高效的优化算法，如微型遗传算法、隔代遗传算法等。其中，隔代遗传算法是在微型遗传算法的基础上加入隔代遗传算子，隔代映射算子的作用是在连续2代最好个体的方向上寻找更好的个体，代替当代最差的个体，从而不仅继承了微型遗传算法种群规模小、基因多样化和全局优化的特点，而且大大提高了收敛的效率［9］。

本文采用隔代遗传算法优化程序，取交叉概率Pc＝0.5，变异概率Pm＝0.01，经过300代优化，结果趋于稳定。

最后优化结果为箱体的轴向壁厚4.0mm，底面壁厚5.18mm。箱体的质量为40kg，箱体最大应力为117MPa，最大变形量为0.099 0mm，第1阶振动频率为146Hz。

2.4 优化结果分析

3种模型结果对比见表3所列。

表3 3种模型结果对比

利用优化的箱体结构尺寸数据在三维软件中重新建模，计算得到新的结构应力云图、变形量云图及第1阶模态振型云图，分别如图6所示。结果显示箱体最大静刚度为0.099 4mm，最大应力为111MPa，第1阶模态的振动频率为145Hz，结果均满足设计的约束条件。

在新的壁厚条件下所得质量、刚度强度及模态结果与优化所得结果误差不超过5%，故优化结果有较高的可信性。

在此结构下，箱体的质量为40kg，与优化前的结构51kg相比，质量减轻了11kg，轻量化程度达到21%。箱体最大应力为117MPa，安全系数为1.3，可以满足材料应力要求。最大变形量为0.099mm，根据该大巴设计标准，箱体最大许可变形量不超过0.20mm，故满足变速箱刚度要求。第1阶振动频率为146Hz，高于箱体振动的安全频率120Hz。

图6 变速箱变形量、应力及第1阶阵型云图

3 结束语

（1）针对某型变速箱的轻量化问题，首先建立了该箱体的有限元模型，研究了箱体的静强度、刚度问题及模态振动特性，在满足强度刚度及模态的要求下提出了优化的必要性，进而以厚度为设计变量，用Fortran语言编写程序，针对箱体的质量做了轻量化方面的优化设计，最终取得了较好的优化结果，箱体质量减轻了21%。

（2）在优化时根据箱体有限元模型计算量大等特点，建立了结构的径向基函数近似模型，避免了优化时重复调用计算量较大的有限元模型的问题，有效地提高了整个优化流程的效率。同时，该优化方法对于较规则的箱式变速器结构轻量化设计具有指导意义。

［1］蔡 锋，张亮亮，刘旌扬.优化设计在汽车零部件轻量化中的应用［J］.汽车技术，2010（4）：25－29.

［2］胡 伟，喻 川，张建武，等.新能源汽车底盘纵臂的轻量化设计［J］.机械设计与研究，2010，26（3）：115－117.

［3］桑 楠，白 玉，杜云峰.基于ABAQUS的汽车前摆臂轻量化设计［J］.长春工程学院学报：自然科学版，2010，11（2）：79－82.

［4］崔 中，文桂林，赵子衡，等.基于区间数的高速磨床主轴系统的不确定性优化研究［J］.湖南大学学报：自然科学版，2010，37（8）：29－34.

［5］穆雪峰，姚卫星，余雄庆，等.多学科设计优化中常用代理模型的研究［J］.计算力学学报，2005，22（5）：608－612.

［6］Jin R，Chen W，Simpson T W.Comparative studies of meta modeling techniques under multiple modeling criteria［J］.Journal of Structural and Multidisciplinary Optimization，2001，23（1）：1－13.

［7］隋允康，李善坡.结构优化中的建模方法概述［J］.力学进展，2008，38（2）：190－199.

［8］文桂林，崔 中，彭克立.基于近似模型的高速磨床零部件结构优化设计研究［J］.中 国 机械工程，2009，20（8）：906－910.

［9］Liu G R，Han X.Computational inverse techniques in nondestructive evaluation［M］.Florida：CRC Press，2003.