POSS对聚乙烯力学性能影响的分子动力学模拟

李君，孙毅，曾凡林

(哈尔滨工业大学航天科学与力学系，黑龙江哈尔滨150001)

多面体低聚倍半硅氧烷(polyhedral oligomeric silsesquioxane，POSS)是一类结构简式为(RSiO 1.5)n(n≥4且为偶数，R为有机取代基团)的化合物.POSS单体可以与有机聚合物进行化学连接而生成POSS有机-无机纳米杂化材料［1］，从而提高聚合物的耐磨性、耐高温性、硬度、强度等一系列的力学性能［2-4］.

POSS对基体材料的性能产生影响的机理缺乏理论.文献［5-6］通过分子动力学模拟方法，计算了材料的多种参数，结论认为POSS单体由于体积巨大，掺杂在材料中阻碍了材料分子的运动，从而使材料的性能得到提高.这可以用来解释增强的原因，但是在聚合物中加入POSS后，有些弹性模量确实得到了增强［7］，但是有些弹性模量反而降低了［7-8］.为了进一步分析POSS对材料改性的原因，本文采用分子动力学方法模拟了聚乙烯(PE)及含有不同POSS比例的杂化聚乙烯(POSS-PE)在不同温度下的行为，计算得到了4种材料的玻璃态转变温度(Tg)及弹性模量.最后通过各部分能量的具体变化来寻求POSS的加入对基体材料力学性能影响的原因.

1 模拟实验

1.1 模型

由于PE的结构简单，模拟起来相对容易，因此选用 PE作为基体材料.而 POSS单体采用T8［CH2CH3］7(CH2)8CH=CH2［9］，其结构如图1 所示.

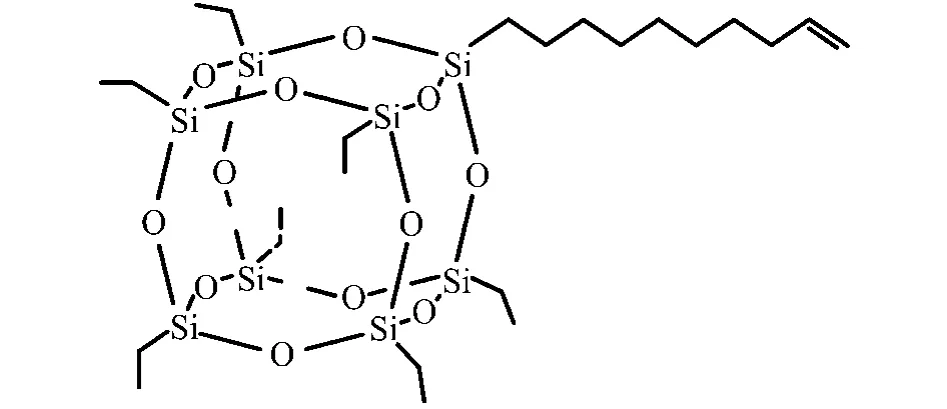
图1 POSS单体结构图(H原子没有标出)Fig.1 Illustration of the POSS unit(H atoms are not shown)

POSS单体通过一系列化学反应与PE主链结合生成的POSS-PE结构如图2所示.

图2 POSS-PE主链结构图(H原子没有标出)Fig.2 Illustration of the POSS-PE chain(H atoms are not shown)

受计算条件所限，在实际模拟中，PE的主链由500个乙烯单体聚合而成，而整个PE模型包括6条主链，采用周期性边界条件［10］打包在一个元胞内.对于POSS-PE，构建了3种含有不同POSS比例的模型，即分别在PE主链上加入2个，4个和6个POSS单体，从而生成3种POSS-PE主链.然后采用周期性边界条件分别将每种POSS-PE主链打包在各自的元胞中，最后生成所需的3种POSS-PE模型.为简便起见，称其为PEII、PEIV和PEVI.4个模型的详细信息如表1所示.

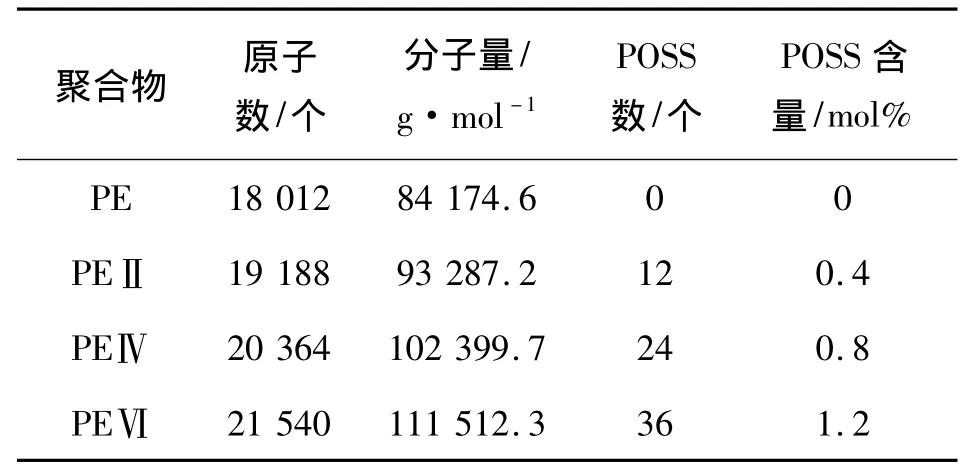
表1 4种聚合物的参数Table 1 Details of the four polymers

1.2 势函数

势函数作为分子模拟的核心，在分子模拟过程中占有非常重要的地位.在本文进行的所有模拟中，都采用CVFF力场［11］作为势函数，因为其形式简单，而且被广泛地应用在聚合物的模拟上［12-15］.

CVFF力场的表达式为

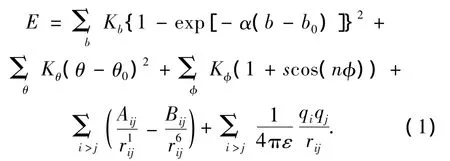
式中:Kb、α是与键类型相关的参数，b0是键的平衡长度;Kθ是与键角类型相关的参数，θ0是平衡键角;Kφ、s、n是与二面角类型相关的参数，是二面角的大小;Aij和Bij为作用系数，不同原子之间的作用系数通常由来计算，rij是 i原子和j原子之间的距离;ε为介电常数，qi和qj分别是第i和j个原子的剩余电荷.剩余电荷采用键增量δij表示原子j对原子i的剩余电荷.在键增量δij中，i表示电荷受体，j表示电荷给体，例如δCH=-0.053，表示碳氢键中氢原子对碳原子的剩余电荷为-0.053，电荷键增量 δij是通过从头计算静电势能得到的.原子i的剩余电荷是所有与其成键的电荷键增量 δij的总和，即同类型原子间键增量为0.模拟过程中用到的参数如表2～6所示.

表2 键长能参数Table 2 Parameters for bond energy

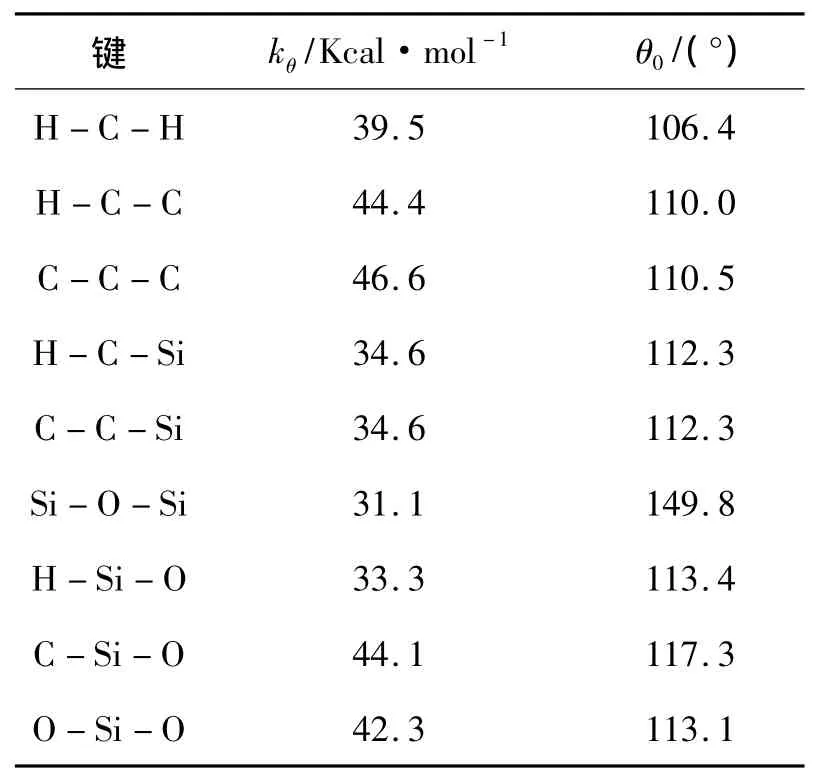
表3 键角能参数Table 3 Parameters for angle energy

表4 二面角能参数Table 4 Parameters for dihedral energy

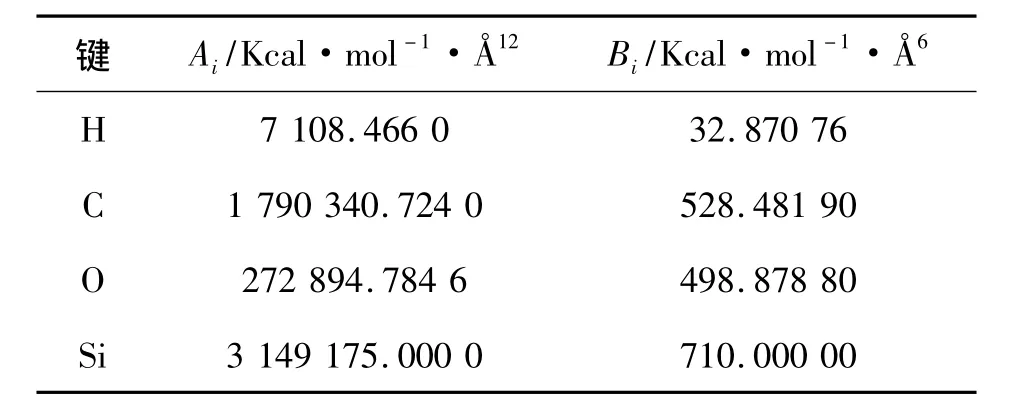
表5 范德华能中的作用系数Table 5 Parameters for van der Waals(VDW)energy

表6 键增量Table 6 Bond increments

1.3 模拟过程

最初，4种聚合物都以大小为0.3 g·cm-3的低密度建立.然后采用模拟退火法，让模型从500 K温度开始，每隔50K通过分子动力学方法弛豫1ns.通过这种方法，使体系的结构逐渐得到优化，从而保证模型的结构更加合理.最终4种材料在50 K下的密度分别为0.89、0.92、0.93 和 0.95 g·cm-3.得到材料的初始模型后，继续以50 K为间隔，从50 K开始一直模拟到400 K.在每个温度下，时间步长取0.5 fs，截断半径取1.2 nm.每次模拟弛豫1 ×107步，结果的后一半用于体积，弹性模量和能量的计算.

所有的模拟均在NPT系综［10］下进行，压强为一个大气压.所用的算法［16］结合了 Nosé-Poincaré控温算法［17］和 metric-tensor控压算法［18］.而时间积分则采用generalized leapfrog算法［19］.以上算法都是保辛的，这样得到的计算结果才是合理的.另外，计算过程中库伦能采用Wolf方法［20］计算.Wolf方法比Ewald方法［10］更加简单，同时又不失准确性，可以大大节省计算时间.

2 模拟结果和讨论

2.1 玻璃态转变温度

玻璃态转变温度Tg是聚合物的一个重要性能指标.以Tg为界，聚合物呈现不同的物理性质，在Tg以下，聚合物处于玻璃态，在Tg以上，聚合物表现出高弹性质.Tg有多种测定方法，在分子动力学模拟中，可以通过体积温度曲线斜率的转折点来确定［21］.

4种聚合物的体积温度曲线如图3所示.图中，每个温度下的体积为单位质量体积的时间平均值，即平均比容.直线通过最小二乘法拟合得到.从图中每2条直线的交点，计算得到4种材料的Tg分别为305.5、305.8、307.7 和302.9 K.对于玻璃态转变温度，如此微小的差别完全可以忽略.也就是说，POSS的加入对于PE的Tg基本没有影响.

图3 体积－温度曲线Fig.3 Specific volume versus temperature for the polymers

与文献［22-24］的结果相比，本文得到的玻璃态转变温度显然偏大.一般说来，聚合物的Tg与结晶度密切相关，结晶度越高，聚合物的Tg越大.而支链的存在会对主链的结晶产生影响，支链越多结晶度越差［25］.本文建立的模型中没有引入支链，因此会大大提高材料的结晶度，从而导致计算得到的Tg偏大.

另外，由于CVFF势缺少非简谐振动项与交叉能量项，对聚合物的动力学模拟结果并不十分精确.尽管如此，势函数对结果的趋势并没有影响，依然可以将其应用于后面的计算.

2.2 弹性模量

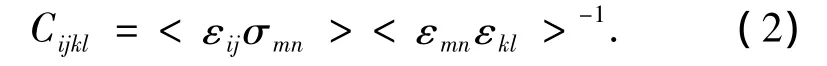
材料的弹性常数可以通过应力应变涨落方法［26］来计算:式中:εij和σij为每一步的应变和应力，＜* ＞表示系综平均，在计算中可以用时间平均来代替.通过式(2)可以得到材料在各温度下的刚度矩阵.由刚度矩阵可以很容易地求出材料的弹性模量［27］.4种聚合物弹性模量随温度的变化曲线如图4所示.

从图4中可以看出，加入少量POSS后，POSSPE的弹性模量会降低，随着POSS含量的增加，POSS-PE的弹性模量达到最大，然后继续加入POSS，弹性模量反而下降.在Tg之前，弹性模量的变化都保持这种模式，在Tg之后，聚合物的弹性模量变得很小，POSS对PE弹性模量的影响也变得很不明显.在300 K时，4种材料的弹性模量分别是0.69、0.67、0.77 和 0.75 GPa.PE 在常温下的弹性模量约为0.9 GPa左右，与本文得到的结果比较接近，在可接受的范围之内.

图4 弹性模量随温度变化曲线Fig.4 Isotropic elastic constants for the polymers with respect to the temperatures

2.3 能量分析

在模拟的过程中，每一步的能量都可以得到，能量的每一部分也可以清楚地获得.材料的结构改变十分明显地表现在能量的变化上，因此，可以通过从能量各部分的变化情况来考察材料结构的变化，进而与材料的性质产生联系.

4种聚合物的各部分能量随温度变化的曲线如图5～9所示，其中，图7、8中的直线是最小二乘拟合的结果.从图中可以看出，键长能和键角能随温度线性变化，在Tg前后，曲线斜率没有任何改变，说明键长和键角的变化并不影响材料的Tg.而库伦能几乎不随温度变化，说明材料的库伦能不受材料结构变化的影响.另外，可以看出各材料库伦能之间相差为常数，约125 eV.这应该是加入0.4 mol%的POSS产生的库伦能改变.在以后的讨论中，就不考虑库伦能的变化.

受Tg影响有明显变化的是二面角能和范德华能.两部分能量在Tg前后，曲线斜率均出现了转折点，与体积温度曲线的情形类似.二面角能的变化代表的是主链结构的扭转，而范德华能的变化则表示主链之间发生相对运动.二者能量的突变表明，主链的扭转和主链之间的相对运动是聚合物产生玻璃态转变主要原因.这一结论与文献［25］中的理论相符合.

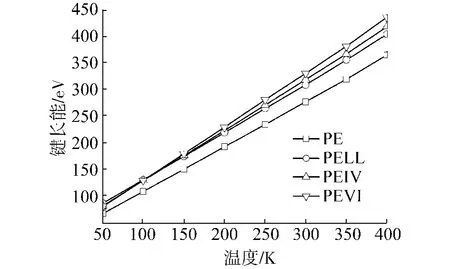
图5 键长能随温度变化曲线Fig.5 Bond energies for the polymerswith respect to the temperatures

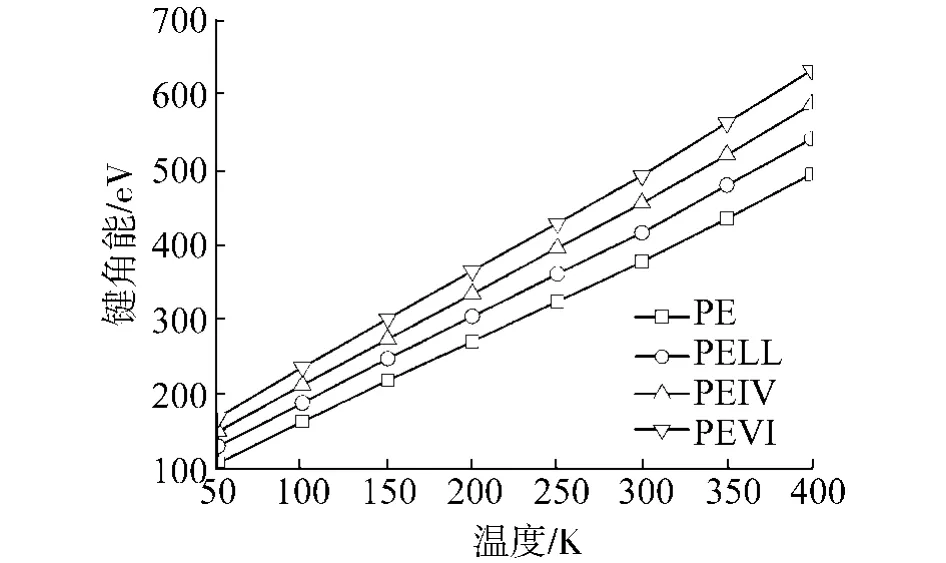
图6 键角能随温度变化曲线Fig.6 Angle energies for the polymerswith respect to the temperatures

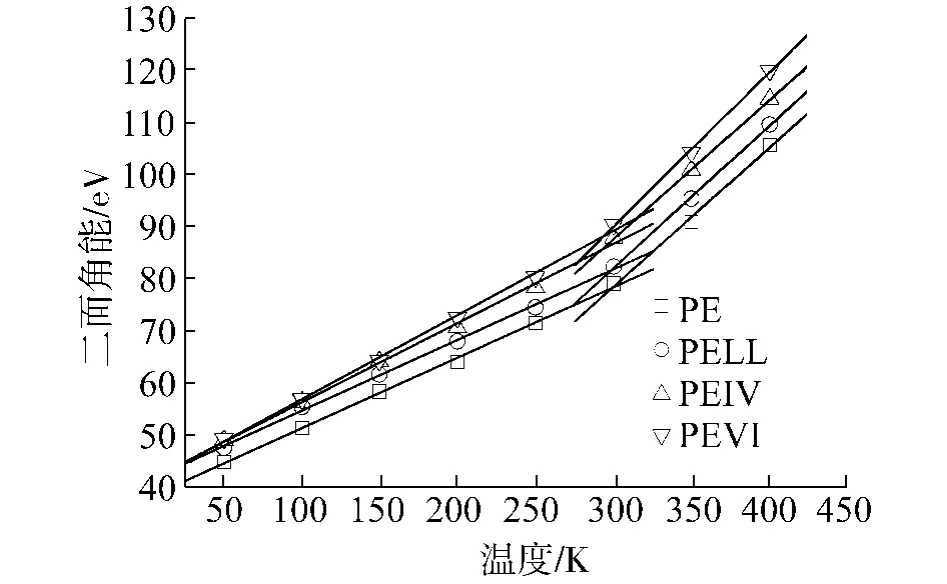
图7 二面角能随温度变化曲线Fig.7 Dihedral energies for the polymerswith respect to the temperatures

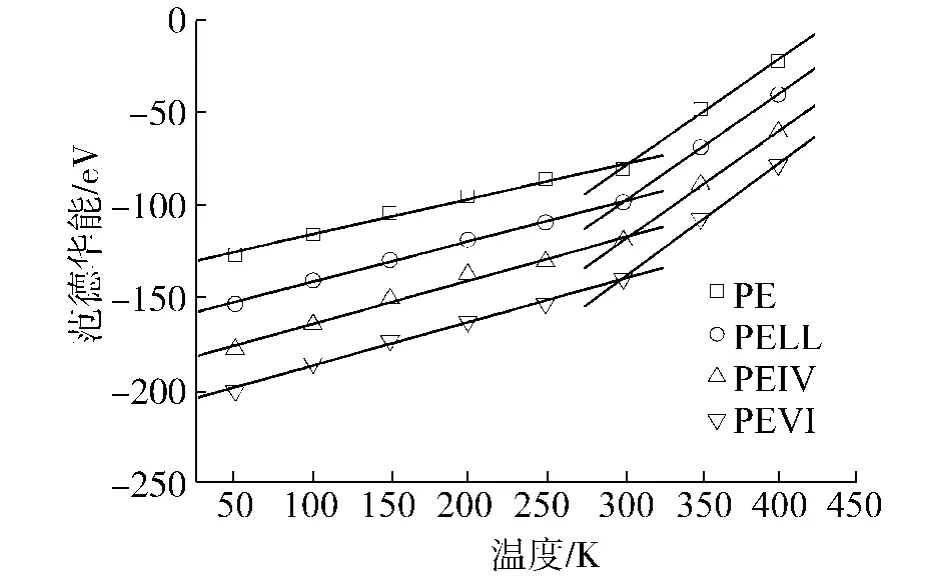
图8 范德华能随温度变化曲线Fig.8 VDwenergies for the polymers with respect to the temperatures

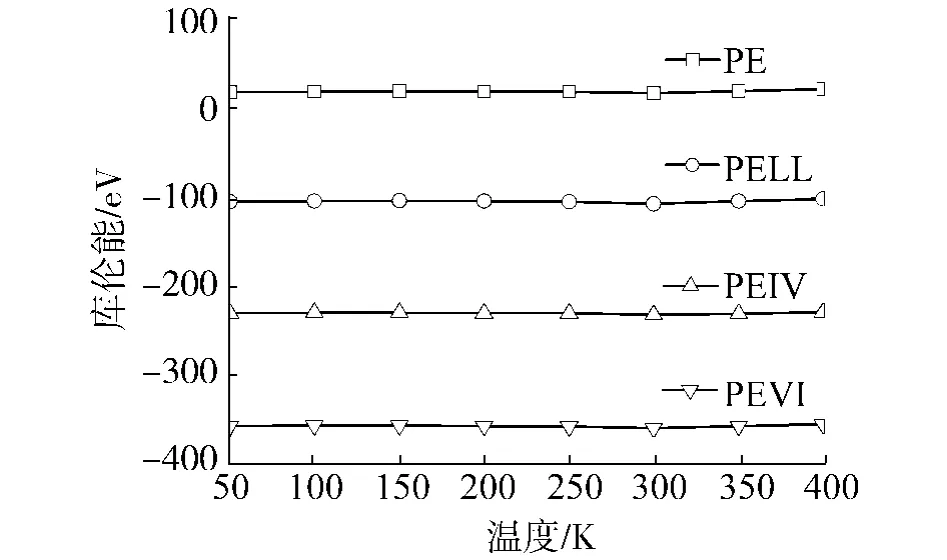
图9 库伦能随温度变化曲线图Fig.9 Coulomb energies for the polymers with respect to the temperatures

由于在所有温度下，POSS-PE的能量趋势是相同的，所以本文以50 K为例，分析POSS单体的加入对基体主链能量的影响.主链的各部分能量与POSS比例的关系如图10所示.从图中可以看出，加入POSS后，POSS-PE主链的键角能，二面角能和范德华能与PE相比变化很小，基本可以忽略.对于键长能，PEIV和PEVI的键长能变化不大，而PEII的键长能有显著提高，说明POSS的加入使基体材料主链的键长被拉长，从而导致结构变得不稳定，使基体的弹性模量减小.PEII相对于PE弹性模量的减小就是由此导致的.

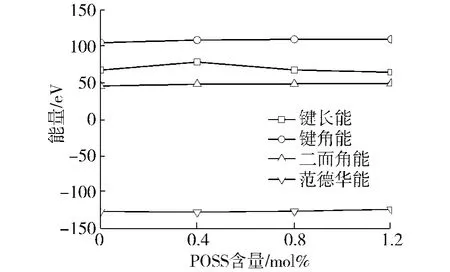
图10 50 K下主链能量随POSS比例的变化曲线Fig.10 Energies of themain chainswith respect to the content of the POSS units at 50 K

图11 平均每个POSS单体与主链之间的范德华能随POSS比例的变化曲线Fig.11 VDwEnergies between the POSS unit and the main chains on averagewith respect to the content of the POSS units

为了更深入地分析POSS的加入对PE的影响，计算得到了POSS单体与基体材料主链之间的范德华能的变化，如图11所示.从图中可以看出，300 K以前，平均每个POSS单体与基体之间的范德华能随POSS比例的增高而增大，在400 K时，能量的变化没有之前显著.范德华能的增加说明POSS与主链之间的距离增加.而POSS与主链距离的增加说明两者的结合减弱.PEIV和PEVI弹性模量在300K之前随POSS比例增加而减小与这个趋势相符合.在300 K之后，POSS对PE的弹性模量影响不大，也与400 K时能量的变化吻合.因此，材料弹性模量增强与POSS和主链之间的相互作用密切相关.由此说来，PEII的增强效果应该最强，而PEVI最弱.但是如前面讨论过的，由于PEII中POSS与主链的强烈吸引，导致主链的键长增加，反而劣化了基体的结构而导致弹性模量减小，最终的结果是PEIV对材料弹性模量的增强效果最大.这样POSS-PE的弹性模量随着POSS比例的增加而变化就解释清楚了.

3 结论

通过分子动力学模拟得到的结果，可以得出以下结论:

1)POSS的加入对于PE的Tg基本没有影响.聚合物在Tg前后，产生了较大的主链扭转和链间相对运动.这一结论与已有的理论相符合.

2)随着POSS比例的增加，弹性模量先出现减小，然后增加，而后再减小.在Tg之前，弹性模量的改变均保持这种模式.而在Tg之后，PE的模量变得很小，POSS的加入对PE弹性模量的改变可以忽略.说明POSS有效地改变了PE在Tg之前的弹性模量.

3)POSS与主链之间的范德华作用是导致POSS-PE弹性模量增加的原因，而PEⅡ相对于PE弹性模量的减小，是因为POSS的加入导致主链键长的增加，而使基体材料结构变差，弹性模量减小造成的.

［1］SANCHEZ C，RIBOT F.Design of hybrid organic-inorganic materials synthesized via Sol-Gel chemistry［J］.NewJournal of Chemistry，1994，18:1007-1014.

［2］MATHER PT，JEONH G，ROMO-URIBEA，etal.Mechanical relaxation andmicrostructure of poly(norbornyl-POSS)copolymers［J］.Macromolecules，1999，32:1194-1203.

［3］FU B X，HSIAO B S，PAGOLA S，et al.Structural development during deformation of polyurethane containing polyhedral oligomeric silsesquioxanes(POSS)molecules［J］.Polymer，2001，42:599-611.

［4］LIU H Z，ZHENG S X.Polyurethane networks nanoreinforced by polyhedral oligomeric silsesquioxan［J］.Macromolecular Rapid Communications，2005，26(3):196-200.

［5］BHARADWAJR K，BERRY R J，FARMER B L.Molecular dynamics simulation study of norbornene-POSS polymers［J］.Polymer，2000，41:7209-7221.

［6］BIZET S，GALY J，GERARD J F.Molecular dynamics simulation of organic-inorganic copolymers based on methacryl-POSS and methyl methacrylate［J］.Polymer，2006，47:8219-8227.

［7］FINA A，TABUANI D，CAMINO G.Polypropylene-polysilsesquioxane blends［J］.European Polymer Journal，2010，46:14-23.

［8］LEU C，CHANG Y，WEIK.Synthesis and dielectric properties of polyimide-tethered polyhedral oligomeric silsesquioxane(POSS)nanocomposites via POSS-diamine［J］.Macromolecules，2003，36:9122-9127.

［9］TSUCHIDA A，BOLLN C，SERNETZ F G，et al.Ethene and propene copolymers containing silsesquioxane side groups［J］.Macromolecules，1997，30:2818-2824.

［10］FRENKEL D，SMIT B.分子模拟-从算法到应用［M］.北京:化学工业出版社，2002:27-29.

［11］MAPLE J R，DINUR U，HAGLER A T.Derivation of force fields formolecularmechanics and dynamics fromab initio energy surfaces［C］//Proc Nati Acad Sci.［s.l.］，1988，85:5350-5354.

［12］LAUTENSCHLÄGER P，BRICKMANN J，VAN RUITEN J.Conformation and rotational barriers of aromatic polyesters［J］.Macromolecules，1991，24:1284-1292.

［13］BHOWMIK R，KATTIK S，KATTID.Molecular dynamics simulation of hydroxyapatite-epolyacrylic acid interfaces［J］.Polymer，2007，48:664-674.

［14］GREATHOUSE JA，ALLENDORFmD.Force field validation formolecular dynamics simulations of IRMOF-1 and other isoreticular zinc carboxylate coordination polymers［J］.JPhys ChemC，2008，112:5795-5802.

［15］HEINZ H，KOERNER H，ANDERSON K L，et al.Force field for mica-type silicates and dynamics of octadecylammoniumchains grafted to montmorillonite［J］.ChemMater，2005，17:5658-5669.

［16］HERNANDEZ E.Metric-tensor flexible-cell algorithmfor isothermal-isobaric molecular dynamics simulations［J］.J ChemPhys，2001，115(22):10282-10290.

［17］BOND SD，LEIMKUHLER B J，LAIRD B B.The nosepoincaremethod for constant temperaturemolecular dynamics［J］.JComput Phys，1999，151:114-134.

［18］SOUZA I，MARTINS J L.Metric tensor as the dynamical variable for variable-cell-shape molecular dynamics［J］.Phys Rev B，1997，55(14):8733-8742.

［19］SUN G.Construction of high order symplectic Runge-Kutta methods［J］.JComput Math，1993，11(3):250-260.

［20］WOLF D，KEBLINSKIP，PHILLPOT S R，et al.Exact method for the simulation of coulombic systems by spherically truncated，pairwise r-1 summation［J］.J ChemPhys，1999，110(17):8254-8282.

［21］HAN JC，GEE R H，BOYD R H.Glass transition temperatures of polymers frommolecular dynamics simulations［J］.Macromolecules，1994，27:7781-7784.

［22］GAUR U，WUNDERLICH B.The glass transition temperature of polyethylene［J］.Macromolecules，1980，13:445-446.

［23］NG SC，HOSEA T JC，GOH SH.Glass transition of polyethylene as studied by brillouin spectroscopy［J］.Polymer Bulletin，1987，18:155-158.

［24］EBERLE R，ANDERSSH，WEISHAUPT K，et al.Anisotropic effects of the glass transition in oriented polyethylene［J］.Europhys Lett，1998，43:201-206.

［25］何平笙.新编高聚物的结构与性能［M］.北京:科学出版社，2009:159-182.

［26］CUIZ，SUN Y，LI J，et al.Combination method for the calculation of elastic constants［J］.Phys Rev B，2007，75(21):214101.1-214101.6.

［27］HADDADIK，BOUHEMADOU A，LOUAIL L，et al.Ab initio study of structural，elastic，and high-pressure properties of rubidiumhalides RbX(X=F，Cl，Br and I)［J］.Phase Transit，2009，82(3):266-279.