印染车间中深浅颜色坯布切换算法模型的实现
2011-08-29周晓慧
胡 颖,周晓慧
杭州电子科技大学信息与控制研究所, 浙江杭州 310018
0 引言
生产过程中的优化调度一直是过程操作中的关键问题,提高生产车间的生产管理水平和生产效率,确保准时交货,对提高企业的市场竞争力具有迫切的现实意义。而当前国内印染企业的生产调度大部分还是由人工来完成,人工调度工作量大、效率低、实时性差,很难适应市场多品种、小批量的生产要求[2]。理论研究方面,现有的印染调度模型对深浅颜色坯布的切换时间考虑甚少,难以应用于实际。本文研究染色工艺的优化调度,通过改进现有模型建立合理的考虑深浅颜色坯布切换时间的优化调度模型,使得模型的使用面更加广泛,更加实用于实际生产过程。
1 优化调度模型
本节中我们将根据印染批处理生产调度的多产品、多工序、顺序加工等调度模型特点,给出基于连续时间MILP数学调度模型的约束条件[1-3]。其中约束(1)-(6)都是现有模型的约束[2],(7)-(9)是改进完善后考虑深浅坯布切换时间的约束。在模型的约束条件中,调度模型主要的决策变量分别是Xijl、Wiu和Siu。它们分别表示一道工序上是否是相邻订单、生产设备上的订单分配和生产设备上的第一个加工的订单分配。
1.1 模型约数函数
1) 在工序上l相邻加工的订单u和v必定分配给同一台生产设备上加工:
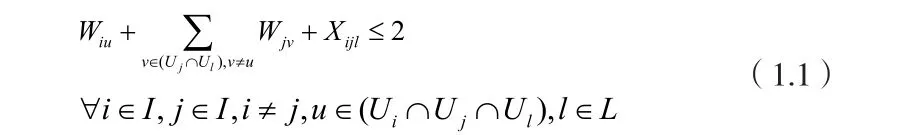
2)在工序l中,生产设备u上除最后加工生产的订单外其余所有订单都有且仅有一个唯一的直接后序订单:

3) 在工序l中,生产设备u上除了第一个被加工的订单外其余的每个订单都有且仅有一个唯一直接前序订单:

4)模型中主要决策变量Wiu和Siu的关系:
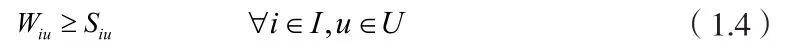
5)在生产设备u上至多有一个初始加工的订单,其中订单集合中的唯一一个订单i是第一个被加工的订单,此时:

6)每道工序中任意一个订单必须分配并只能分配给一台唯一的生产设备加工:
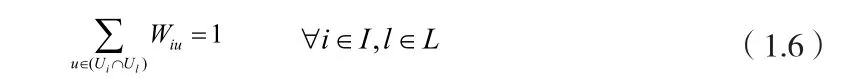
7)当一个订单i的生产工序m是在生产工序l前面的,则有此订单i在工序l中的起始时间必须大于或等于此订单i在工序m中加工完成后的时间:

8)同一道工序上两个具有直接前后续关系的深浅订单j中后序订单的起动时间大于等于订单i在生产设备u上的加工运行时间与此工序设备u上订单i和订单j切换所需时间即Ciju的和。式中M为足够大的正数,保证订单j和订单i在工序l为直接前后序订单:
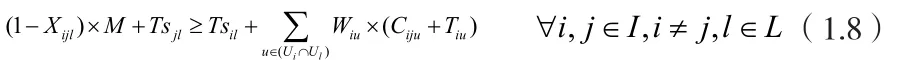
9)订单的实际延期是指订单的完成时间和订单的交货期的Di差值:
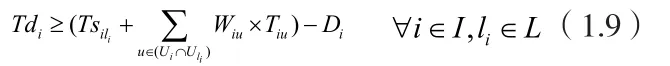
1.2 模型目标函数
为了降低成品生产后的高额库存成本以及减少企业的流动资金,印染行业对印染订单交货期的准时要求非常严格。本调度模型的目标函数是使订单在最大限度的接近订单交货期:

调度模型中所求的最优调度解的目标就是使得目标函数式(1.10)取到最大值。式中的N是个足够大的参数,这样就迫使订单的延期总是最小;而参数Hil是用来区分在最后工序中各订单执行的优先后次序的,此参数是由Pinto和Grossmann(1995)[3]提出来的:

式中Max( d )指的是印染生产中所有被调度的订单的交货期的最大值,而Ord( l )指订单生产工序的工序号。
2 模型求解与结果分析
印染生产是一种将原材料转化为产品的增值生产,原材料为坯布以及染化料、烧碱双氧水等一些印染助剂,产品为面料。整个印染工艺基本过程分为前处理、染色和后整理[2-3],不同的订单产品由于生产加工的坯布不同一般有着各自特定的工艺和工序路线,其中印染工序上深浅颜色订单的切换时间是批处理生产调度问题中必须要考虑的一个重要方面[1-2]。表1给出了印染生产的工序流程和每道工序包含的设备号。在印染车间坯布加工生产中,假设每道工序都只包含一台设备,对应的设备号就是工序号。

工序号 工序名 包含的设备号1翻缝、烧毛 1 2退浆、煮练、氧漂 2

表1 印染生产设备信息
订单的基本信息包含了坯布类型,坯布颜色,坯布长度,订单的交货期,见表2。

表2 订单的相关信息

表3 订单相互之间的切换时间(有直接前后序关系时)
实例中四个订单相互之间的如果有直接前后序时的切换时间见表3。此表说明在工序7即染色工序上,由于订单1是石头色的全棉帆布,在四个订单中颜色最浅,所以当其他订单作为订单1的后续订单时,机床不用清洗,切换时间都为0;订单2是藏青色的全棉府绸,在遇到黑色的订单3时不用清洗,因为黑色是更深的颜色,而后续订单是石头色的订单1和灰色的订单4时则
需要清洗,清洗时间分别为13个小时和10个小时;订单3和订单4同理。
将实例订单数据以及印染生产车间的生产相关数据以ILOG OPL的语义形式导入工程中的数据文件,然后运行模型求出实例的调度结果集,最后根据其调度结果集绘制出实例的生产甘特图,如图1所示,甘特图清晰的显示出运用模型后调度的结果。

图1 运行结果甘特图
3 结论
本文着重针对印染生产中的染色环节生产工艺进行研究,在现有模型的基础上,充分考虑深浅坯布切换,建立了考虑深浅坯布切换时间的优化调度模型,将数学模型转换为ILOG CPLEX的可求解模型,用ILOG的CPLEX求解该模型,验证了该模型的有效性和可行性。
[1]郑俊玲.基于连续时间MILP批处理调度研究以及在印染行业的应用[D],2008:30-33.
[2]梅红,张智丰.基于连续时间的生产过程优化调度[J].浙江大学学报,2010:1423-1427.
[3]Gooding W.B.,Pekney J.F.,McCroskey P.S.,Enumerative Approaches to Parallel Flowshop Scheduling via Problem Transformation[J].Computers and Chemical Engineering,1994,18:909-920.
