关于四边形剪拼的探究
2011-08-27张昌林襄州区黄集镇初级中学湖北襄阳441123
●张昌林 (襄州区黄集镇初级中学 湖北襄阳 441123)
一小学生放学回家说:“今天的作业是剪图形,老师让我们剪三角形、正方形、长方形、平行四边形、梯形……,然后把剪好的图形拼成新的图形.”笔者发现剪拼图形挺有意思,于是做了一些研究,与大家分享.
注这里讲的“剪”,只能沿直线剪;这里讲的“拼”,指图形拼完后不能有重叠部分,也不能有剩余部分.
1 平行四边形的剪拼
1.1 平行四边形剪拼成三角形
平行四边形剪拼成三角形主要用“面积不变”的思路,有2大类方法,每一大类都有无数种拼法.
方法1 如图1,在▱ABCD中,点E是AB的中点,作射线DA,CE,2条射线相交于点D'.易证△AED'≌△BEC,将△BEC绕点 E旋转 180°与△AED'重合,这样将▱ABCD沿CE剪开就可以拼成△DCD'.
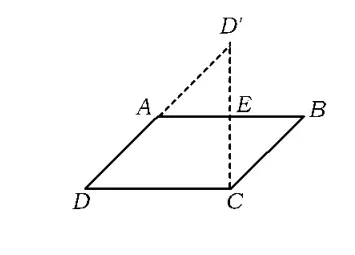
图1
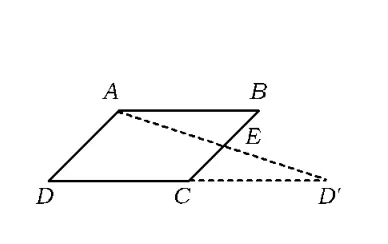
图2
方法2 如图2,在▱ABCD中,也可先找到BC的中点E,其他作法同上.
是否只有这2种方法呢?用动态的观点研究该问题,有方法3如下:
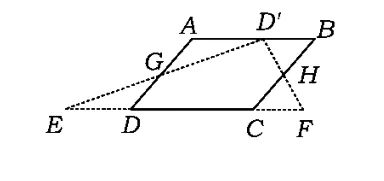
图3
图4
方法3 如图3,点G,H分别是AD,BC的中点,D'是AB上任意一点(动点),作射线D'G,D'H,分别交直线 DC于点 E,F.易证△DGE≌AGD',△HBD'≌△HCF,这样▱ABCD就可以剪拼成△EFD'.当点D'在AB上移动时,产生的△EFD'随之变化,因此产生的△EFD'就有无数种剪拼方法.
当点D'在AB上运动到如图4所示的位置时,△EFD'为锐角三角形;当点D'在AB上运动到如图5所示的位置时,△EFD'为直角三角形;当点D'在AB上运动到如图6所示的位置时,△EFD'为等腰钝角三角形.当点D'在AB上运动时,△EFD'能否为等边三角形?若不能,请说明理由.
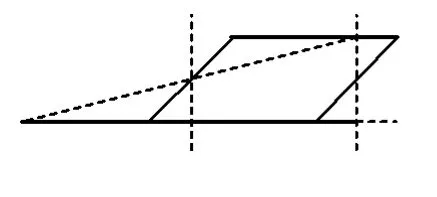
图5
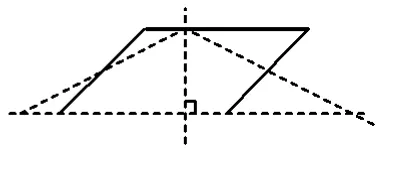
图6
同样地,用动态的观点研究该问题,又有方法4,方法4实际上是方法1的一般化推广.
同理,可以将动点D'选在BC(或AD)上,方法原理同上.
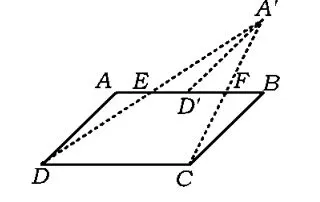
图7
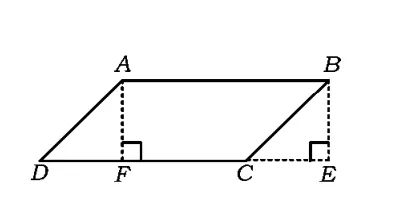
图8
1.2 平行四边形剪拼成长方形
如图 8,过点 A作 AF⊥DC于点 F.易证Rt△ADF≌Rt△BCE,将△ADF剪下平移到△BCE的位置就拼成了长方形.
1.3 平行四边形剪拼成正方形
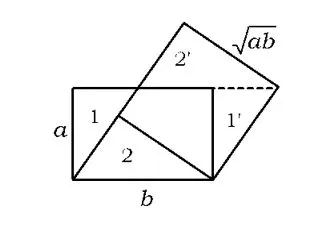
图9
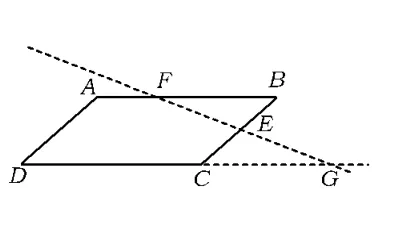
图10
平行四边形剪拼成正方形的过程较复杂,要先将平行四边形剪拼成长方形,再把长方形剪拼成正方形.如图9所示,用“面积不变”的思路,可将给定的长方形剪拼成正方形.请读者探讨有没有更好的方法.
1.4 平行四边形剪拼成梯形
同样地,用动态的观点研究该问题,用“面积不变”的思路,把平行四边形剪拼成梯形.如图10,点E是BC的中点,点F是AB上任意一点(F不与点A,B重合,思考为什么?).易证△FBE≌△GCE,将△FBE剪下使它和△GCE重合即拼成了梯形AFGD.因为点F在AB上移动,所以有无数种剪拼梯形的方法.当点F移动到点A的位置时,平行四边形可剪拼成三角形,即1.1中的方法1;当点F移动到如图11所示的位置时,可剪拼成直角梯形;当点F移动到如图12所示的位置时,可剪拼成等腰梯形.
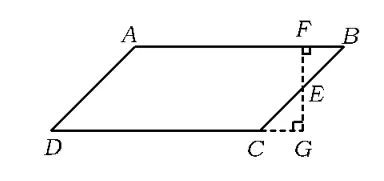
图11
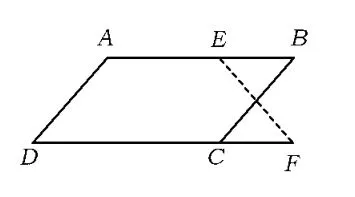
图12
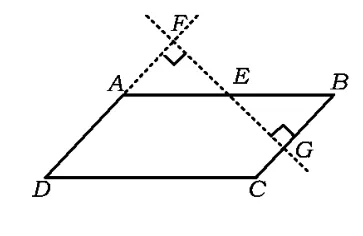
图13
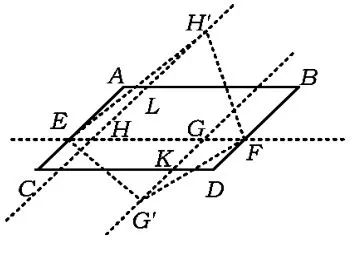
图14
在▱ABCD中,点E为AB的中点,G为BC上任意一点,G在BC上运动(不包括点B,C),原理同上也可以剪拼成梯形.因为点G在BC上运动,所以有无数种剪拼成梯形的方法.特别地,当G运动到如图13所示的位置时,可剪拼成直角梯形.
1.5 平行四边形剪拼成任意四边形
如图14,在▱ABCD中,点E是AC上任意一点,过点E作AB的平行线,交BD于点F.在线段EF上任取2个点G,H(不包括点E,F),分别过点G,H作AC的平行线交CD于点 K,交AB于点L,作点H关于AB的反射点H',作点G关于CD的反射点G'.易证图14中的相关三角形全等,从而剪拼成功.因为点E在AB上移动,点G,H也随之移动,所以有无数种剪拼成梯形的方法.
2 任意四边形的剪拼
2.1 任意四边形剪拼成平行四边形
将1.5平行四边形剪拼成任意四边形的过程反过来,就是将任意四边形剪拼成平行四边形的方法.
2.2 任意四边形剪拼成长方形
在图14 中,让 GG'⊥EF,HH'⊥EF,剪拼的结果就是长方形.
3 梯形的剪拼
3.1 梯形剪拼成平行四边形
如图15,在梯形ABCD中,点H是BC的中点,过H作AD的平行线交AB的延长线于点E,交DC于点G.易证△HEB≌△HGC,将△HGC绕点H旋转180°到△HEB的位置,就剪拼成了▱AEGD.同理,也可以如图16所示那样剪拼.
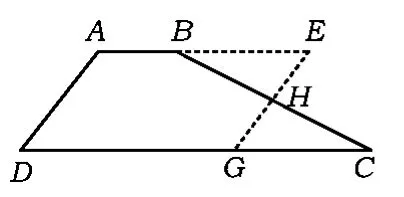
图15
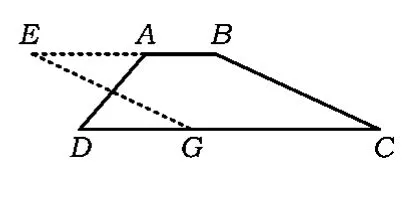
图16
3.2 一般梯形剪拼成等腰梯形
如图17,作梯形ABCD中位线的中垂线,沿中垂线将梯形对折(即作点D关于中垂线的对称点G),点H是腰BC的中点,射线GH交AB的延长线于点 E.易证△BEH≌△CGH,AD=EG,从而剪拼成功.同理,也可以如图18所示那样剪拼.
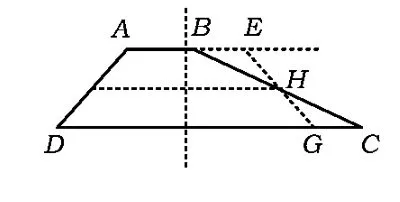
图17
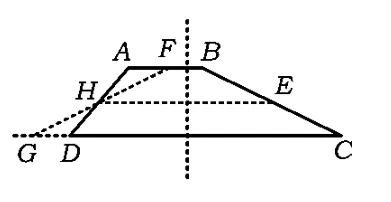
图18
3.3 梯形剪拼成长方形
可以先将梯形剪拼成平行四边形,再将平行四边形剪拼成长方形.或者用2.2任意四边形剪拼成长方形中的方法.
3.4 特殊梯形的特殊变化
底角均为60°的等腰梯形变为等边三角形.图19到图24是剪拼过程的示意图,供读者研究.
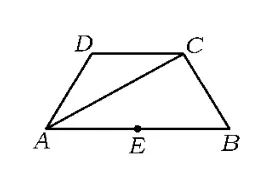
图19
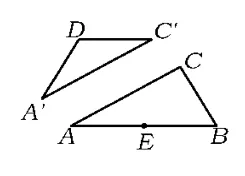
图20
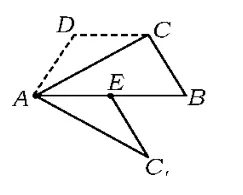
图21
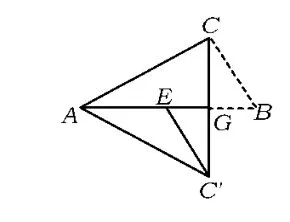
图22
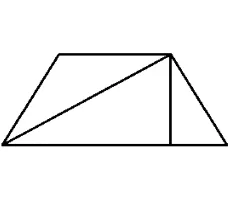
图23

图24
4 2个正方形的剪拼
2个正方形剪拼成1个正方形,这个问题简称“两方拼一方”,人教版数学8年级课本上有关于“两方拼一方”的知识阅读,方法不止一种.笔者研究了几种方法,供读者欣赏.
如图25,边长分别为a,b的2个正方形连成一体,能否在上面画2条直线,沿直线把图形分成几块,然后拼成一个正方形而无剩余.
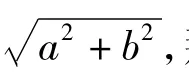
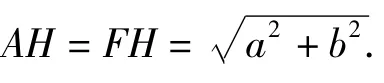
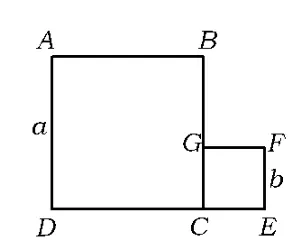
图25
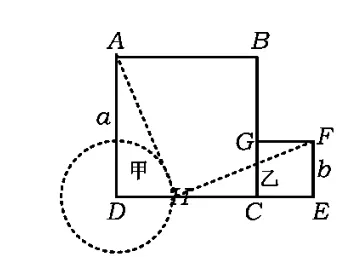
图26
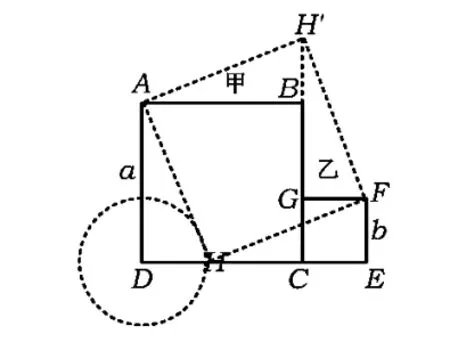
图27
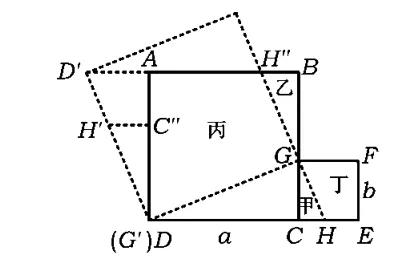
图28
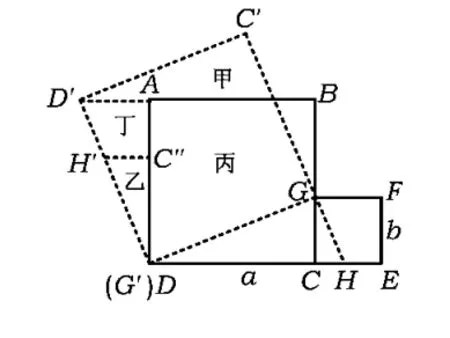
图29
方法3 剪拼过程如图30所示.
看似简单的剪拼问题,充满了数学思考和智慧,亲爱的读者朋友你会了吗?
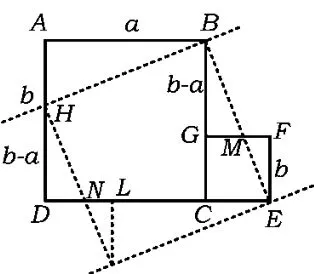
图30
