由“教材”到“学材”的创新构想
2011-08-27中峰镇中心学校湖北竹溪442300魏祖成竹溪县教研室湖北竹溪442300
●甘 霖 (中峰镇中心学校 湖北竹溪 442300) ●魏祖成 (竹溪县教研室 湖北竹溪 442300)
数学例题、习题课教学是数学教学的重要组成部分,是学生理解、掌握和应用数学概念、法则、性质、定理的必要过程,是学生感悟数学思想方法、发展数学思维、培养创新意识和实践能力的必要过程.在初中数学例题、习题教学中,教师要根据学生需要,对教材中的“例题、习题资源”进行有效处理和二度开发,这好似大厨将“家常小炒”加工成“满汉全席”,色、香、味俱全才能让人吃得轻松、愉快.如何将“家常小炒”做成新鲜、可口、让学生爱不释手、垂涎欲滴的“满汉全席”?这就需要教师在钻研教材上下足功夫,充分理解教材例题、习题的设计意图,加以组合、整理、补充、延伸、拓展和变式,设计出学生喜欢的数学习题,培养学生内在的数学情感和智慧.
1 加一点“诱饵”,激发学习兴趣
人本主义教育家罗杰斯说过,真实的问题情境和活动是最能引起态度和个性情绪的学习方式.结合教材例题、习题的基本内容,配上一些符合学生特征的教学情景,使学生的情绪受到感染,利用情感对认知学习的引导作用,驱动、诱导学生的学习动机.
案例1 人教版数学七年级下册第26页第6题第(2)小题:如图1所示,AB∥CD∥EF,那么∠BAC+ACE+∠CEF = ______度.
在教学时可创设情境,巧加“诱饵”——会跳舞的平行线,即将一根橡皮筋系在AB,EF同侧的2个端点上,手拿橡皮筋,改变手势和步伐,可得如下变式:
(1)勇往直前,势不可挡.如图2所示,AB∥EF,求证:∠ACE=∠A+∠E.
(2)平移一步,灵动跳跃.如图3所示,AB∥EF,求证:∠CAB=∠C+∠E.
(3)进而则移,婀娜多姿.如图4所示,AB∥EF,求证:∠E=∠A+∠C.
(4)前进两步,姿势优美.如图5所示,AB∥EF,求证:∠1+∠2=∠BCF-∠BDF.
(5)连续跳动,梦幻变化.
①如图6所示,AB∥EF,求证:∠1+∠2+……+∠n=(n-1)×180°;
②如图7所示,AB∥EF,求证:∠1+∠3=∠2+∠4;
③如图8所示,AB∥EF,根据②的证明猜想你发现了什么结论?

图1
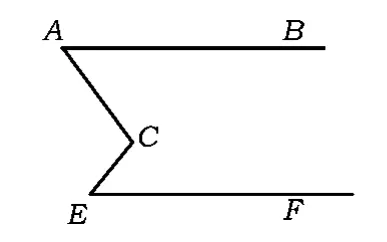
图2

图3

图4
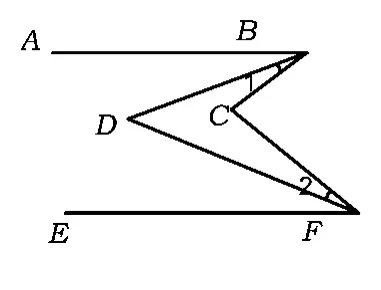
图5
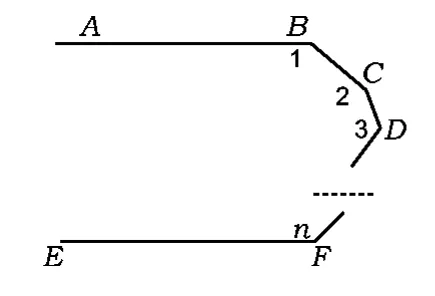
图6
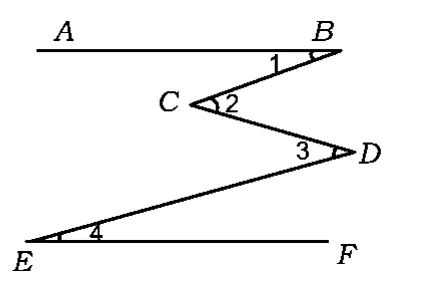
图7

图8
以上5个变式,通过创设问题情境,对课本习题进行创新再探,在保留原题设的前提下,重新创设问题情景,添加情景“诱饵”,将问题逐步引申、挖掘,深化题目的丰富内涵,对培养学生的学习兴趣大有裨益.
2 改一点“口味”,培养数学情感
蛋糕有香草、抹茶、红豆等多种口味,让人意犹味尽、回味无穷.同样地,在学习中学生喜欢多种不同“口味”的习题.教师在教学中要创造性地改编、引申教材中的例题、习题,给例题、习题换新颜,改口味,让学生在解题过程中体验挑战思维带来的喜悦,培养数学情感.
案例2 人教版数学九年级下册第32页第6题:如图9所示,用一段长30 m的篱笆围成一个一边靠墙的矩形菜园,墙长为18 m,求矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
这是一道二次函数综合应用题,蕴涵了方程、函数及数学建模思想.从题目所给的条件、求解的结论、实际的情景、不同的方案等方面去归纳总结,可改编和设计出不同的问题,做到一题多变,既培养了学生运用各种思想方法解题的能力,又建立了知识之间的联系,有利于激发学生的学习兴趣和勇于探索的个性品质.对于该题可作如下“口味”的改变,编制出让学生“爱吃”的好题.

图9

图10
(1)墙长有无限制.
例1 如图10所示,有长为24 m的篱笆,一面利用墙(墙的最大可利用长度a为10 m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
①求S与x的函数关系式.
②如果要围成面积为45 m2的花圃,AB的长是多少.
③能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
例2 利用一面墙(墙的长度不超过45 m),用80 m长的篱笆围一个矩形场地.①怎样围才能使矩形场地的面积为750 m2;
②能否使所围矩形场地的面积为810 m2,为什么?
(2)中间有无隔栏.
例3 要建一个长方形的养鸡场,鸡场的一边靠墙(墙长足够长),如果用50 m长的篱笆围成中间有一道篱笆(长度为x m)的养鸡场.
①要使鸡场的面积最大,鸡场的长应为多少;
②如果中间有n(n>1)道篱笆隔墙,要使鸡场的面积最大,鸡场的长应为多少;
③比较①②的结果,你能得到什么结论?
(3)面数是否变化.
例4 如图11所示,用长为18 m的篱笆(虚线部分),2面靠墙围成矩形苗圃.
① 设矩形的一边长为x m,面积为y m2,求y关于x的函数关系式,并写出自变量x的取值范围;
②当x为何值时,所围苗圃的面积最大,最大面积是多少?
(4)形状发生改变.
例5 如图12所示,某学校在绿化校园时计划利用矩形场地的一角,怎么利用边缘2边(不考虑第三边AB)才能使所建花圃的面积最大,并求出最大面积(精确到1 m2).
(5)设计最佳方案.
例6 某校数学研究性学习小组准备设计一种高为60 cm的简易废纸箱,废纸箱的一面利用墙,放置在地面上,利用地面作底,其他的面用一张边长为60 cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.

图11

图12
①该小组通过多次尝试,最终选定3个简便且易操作的截面图形(见表1),根据这截面图形面积y cm2与x cm(见表1截面图形所示)的函数关系式绘制出图像,请你根据有关信息,在表1中空白处填上适当的数(式),并完成y取最大值时的设计示意图.
②在研究性学习小组展示研究成果时,小华同学指出:图中“底角为60°的等腰梯形”的图像与其他2个图像比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.

表1 横截面图形与函数关系式
(6)容积能否最大.
例7 某农户计划用现有的一面墙修4面墙,建造如图13所示的长方形水池,培育不同品种的鱼苗,他已备足可以修高为1.5 m、长为18 m的墙的材料准备施工,设图中与现有一面墙垂直的3面墙的长度都为x m,即AD=EF=BC=x m(不考虑墙的厚度).
①若想水池的总容积为36 m3,x应等于多少;
②求水池的总容积V与x的函数关系式,并直接写出x的取值范围;
③若想使水池的总容积V最大,x应为多少,最大容积是多少?
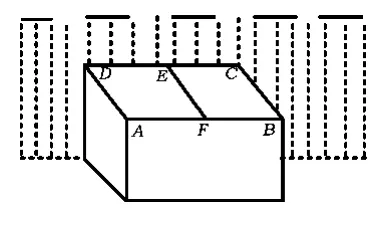
图13
3 变一点“花样”,发展思维品质
教学中,灵活多变的习题设计,能使学生在思维过程中不断接受智慧的挑战,思维的深度和广度得到提高.学生享受智慧带来的成功和愉悦的同时,思维的灵活性和敏捷性得到发展,思维品质得以提升和飞跃,变一点“花样”,设计出学生“跳一跳”就能摘得到的“桃子”.
案例3 人教版数学八年级下册第110页第7题:已知四边形ABCD中,AD∥BC,点M是AD的中点且MB=MC.求证:四边形ABCD是等腰梯形.
此题是一道“条件不充分”的习题,可引导学生寻找“充分条件”的同时,变一点“花样”,作以下思维拓展:
思维拓展1将原题的条件改变,把“点M是上底的中点”变为“下底的中点”,挖掘内在联系.
思维拓展2将特殊条件一般化,把“点M是梯形底边上的中点”变为“梯形外部的点”,探究上述结论是否成立.
思维拓展3将特殊条件一般化,把“点M是梯形底边上的中点”变为“梯形内部的点”,探究上述结论是否成立.
思维拓展4将结论和条件互换位置,把要证明的结论“等腰梯形”作为条件,探究新的结论,从而提高学生的应变能力.
思维拓展5变换条件和结论,把“底边上的中点”变为“2个点”,2腰由“已知相等”变为“结论求证”,提高探索能力.
思维拓展6适当改变已知条件,探索新的结论,从而培养思维的发散性.
例8 已知梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,点E是MB的中点,点F是MC的中点,点N是BC的中点.
(1)求证:四边形MENF是菱形;
(2)当△MBC是什么三角形时,四边形MENF是正方形,并猜想梯形的高与下底之间的数量关系.
思维拓展7变换题型,将证明题改为探索题,探索新的结论是否成立,从而培养思维的发散性.
例9 已知梯形ABCD中,AD∥BC,M是底边AB上的点,给出下面3个论断:①AB=CD;②AM=DM;③BM=CM.请你以其中的2个论断作为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.
已知在梯形ABCD中,AD∥BC,M是底边BC上的点,_______________,求证:________________.
简析 该题从所给的论断入手,不断变换题目的条件与结论,由浅入深,循序渐进,层层深化,既沟通了知识之间的联系又训练了发散思维.
符合题意的情形有3种情况,即①,②→③;①,③→②;②,③→①.
在教学时,如能在例题、习题的解答后做进一步深入研究,便能发现一些很有趣的新知识或好方法,使解答数学问题的过程变成探究、发现的过程,将思维变成流动、活跃的过程,可使学生时时处在一种愉快的探索知识的状态中,从而充分调动学生的积极性,启发学生的思维,提高学生的解题能力和探索能力.
4 增一点“配料”,提升数学能力
在例题、习题教学中,要对学生解题过程中可能出现的困难做充分估计.对于较难理解的知识点,要有针对性地做好铺垫,使解题过程水到渠成.
案例4 人教版数学九年级上册“证明三角形的中位线定理”的教学.
师:如图14所示,在△ABC中,D,E分别是AB,AC的中点,则DE是△ABC的中位线.你能发现哪些结论?
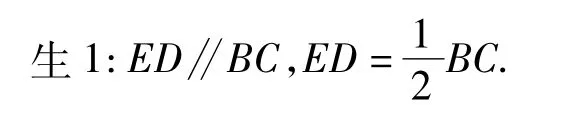
师:如果要证明“三角形的中位线平行于第三边,且等于第三边的一半”这个命题,能把文字语言转化为数学语言吗?
师:很好,能证明吗?
(一学生板演.)
师:还有不同的证法吗?
生3:利用△ADE∽△ABC可证.
师:谁能简述一下证明过程?

图14

师:很不错,还有不同的想法吗?

师:很精彩,连老师也没有想到用这种方法.
在以上的课堂教学中,教师不失时机地问了一下“还有不同的想法吗”,增加了解题的“配料”,学生的精彩发言为整个课堂增加了亮色,这种证明三角形中位线定理的方法连教师都没有想到!
