基于MASTA和ANSYS的行星传动柔性分析
2011-08-26王明成石彦辉
刘 越,毛 明,王明成,石彦辉
LIU Yue, MAO Ming, WANG Ming-cheng, SHI Yan-hui
(中国北方车辆研究所 车辆传动重点实验室,北京 100072)
0 引言
利用计算机仿真进行机械结构设计是现代制造领域的重要方法之一,其目的是优化产品结构,减少研发成本,缩短研发周期。行星齿轮传动具有体积小、传递功率大、受载均匀等定轴传动无法比拟的优点,已经越来越多的出现在现代车辆之中。在长期的工作实践中发现,行星传动机构在工作中损坏主要有以下三种形式[1]:
1)太阳轮、行星轮啮合损坏,主要表现为齿根折断、齿面点蚀等;
2)行星架在轴颈处扭断;
3)行星齿轮内的滚针轴承损坏,主要表现为轴承烧坏、磨损。
显然,以上三种设计方法各有利弊,综合运用上述方法才可达到较好的效果。本文利用专业设计软件MASTA对行星传动机构进行建模,并在有限元软件ANSYS中运用子结构法提取行星架的刚度矩阵和节点位置信息,将刚度矩阵和节点位置信息导入MASTA模型,对行星传动机构进行柔性分析,并将分析报告作为边界条件导回行星架的有限元模型,以实现对行星架的有限元分析。这种方法不仅解决了以往行星架有限元分析时,由于行星架受力变形,导致边界条件不易确定的问题,而且可以得到考虑行星架实际刚度的齿轮安全系数和损伤率,计算结果比较准确。
1 设计参数和工况
2K-H行星齿轮传动效率高、重量轻、结构简单、制造方便,传递功率范围大,并且轴向尺寸小,因而在机械传动中应用最广[2]。
行星机构既可串联为传动系中的增速、减速环节,也可单独用作车辆传动系中轮边减速器或功率分流汇流机构[3]。轮式车辆轮边减速器和履带车辆的行星机构侧减速器一般将齿圈固定,功率从太阳轮输入,由行星架输出,结构简图如图1所示。
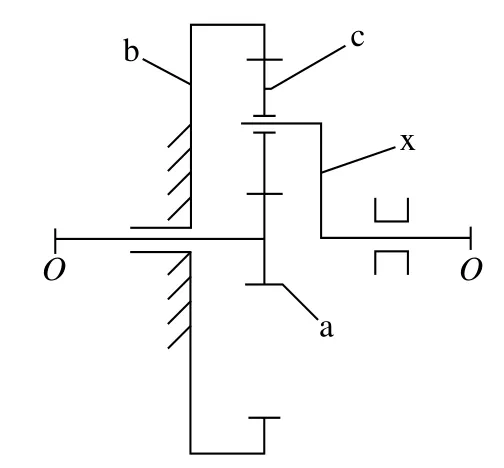
图1 2K-H行星齿轮传动机构
本文以某车侧传动行星机构减速器作为研究对象进行分析,传动比为4.44,行星轮个数np= 4,表1为行星机构各齿轮的基本参数,表2为减速器各档的工作情况。
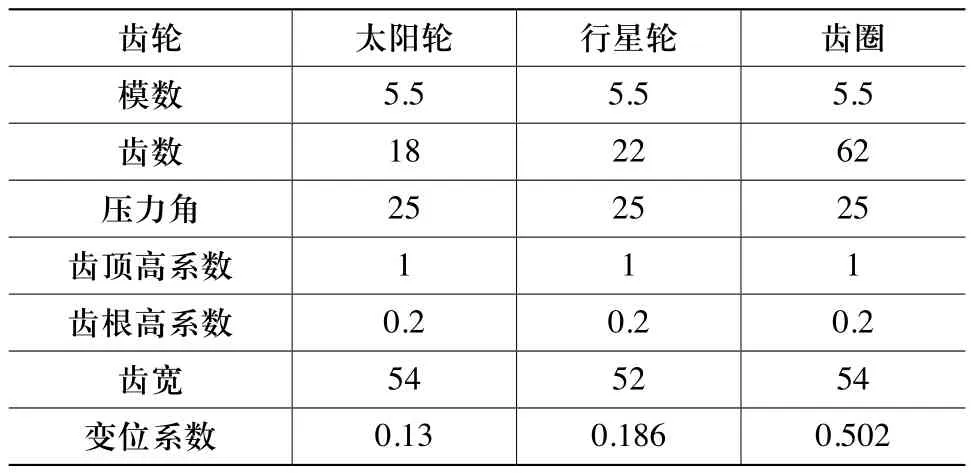
表1 行星齿轮基本参数
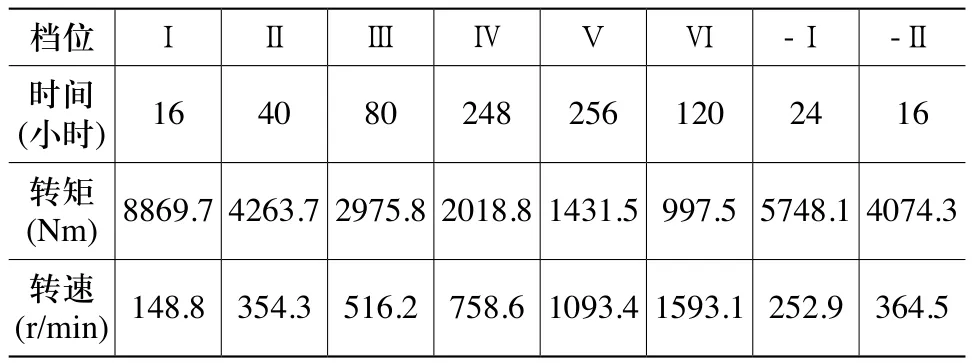
表2 档位情况
2 分析理论
2.1 子结构法介绍
本文运用子结构分析法求解行星架刚度矩阵,所谓子结构技术就是将一组单元用矩阵凝聚为一个单元过程的技术,这个单位称为超单元。超单元可以像其他单元类型一样使用,区别在于必须进行结构生成以产生能够利用的超单元[5]。使用子结构分析法主要优点是节省机时,将大规模的矩阵计算进行分块处理,并且对于重复的结构,生成超单元,然后放在不同的位置,可以节省计算时间。由于行星架具有明显的对称性,因而采用子结构法可以大大缩短计算时间。
2.2 位移法有限元分析理论
在位移法的有限元分析中,计算单元的刚度矩阵是有限元分析的重要一步。由节点平衡方程建立线性方程组时,节点平衡方程中未知的节点力是借助单元刚度矩阵消除的,而线性代数方程组中总体刚度矩阵是由单元刚度矩阵叠加而成的,因此单元刚度矩阵是一个十分重要的特征[4]。
单元刚度矩阵表达单元抵抗变形的能力,其元素值为单位位移所引起的节点力,单元节点力与节点位移的关系如式(1)所示:
医护英语的教学目的是培养具有专业学科知识又有外语技能的复合型人才,其教学逐渐成为医学院校英语教学的一个重要组成部分。随着大数据、人工智能时代的到来,教学与学习方式发生了翻天覆地的变化[1]。如何顺应时代潮流,利用智能互联网技术来推进医护英语教学的创新和发展,提高医护英语教学质量和效果是医护英语教学者所面临的新挑战。笔者在安徽中医药高等专科学校一年的医护英语教学实践中尝试了“智慧课堂”的教学模式,并取得了比较好的教学效果。

式中,Fe为单元节点力,Ke为单元刚度矩阵,δe为单元节点位移。
总体刚度矩阵是由全部的单元刚度矩阵升阶后叠加的总和,计算机一般采用大域变换矩阵法对单元刚度矩阵升阶,结构总体刚度矩阵K与单元刚度矩阵Ke之间的关系如式(2)所示:
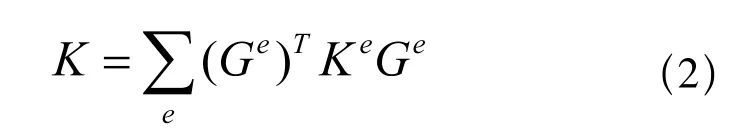
式中,Ge为单元大域变换矩阵。
另外,总体结构的荷载矢量、位移矢量与单元荷载矢量、位移矢量之间的关系如式(3)、式(4)所示:
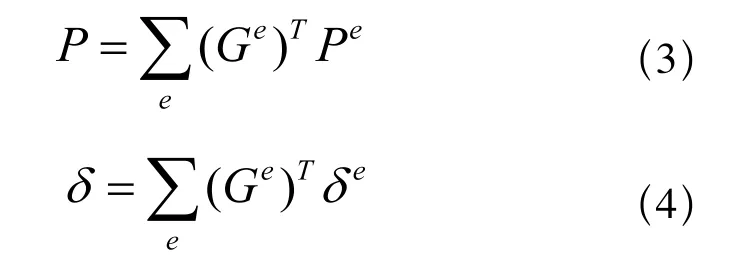
求出各单元的刚度矩阵,利用大域变换法求出结构总体刚度矩阵K,引入边界条件P,得到由节点平衡方程建立的线性代数方程如式(5)所示:

式中,P 为全部节点载荷组成的列阵,δ为全部节点位移组成的列阵。
由式(5)求解全部节点的位移,进而得到单元的应力和应变。
3 行星传动机构的柔性分析
3.1 MASTA原始模型
MASTA是一款功能强大,覆盖面广,实用性强的集选配、设计、制造为一体的传动系统大型专用软件。它具有强大的参数化建模功能和智能化设计功能,只需要输入参数或对参数进行修改便可完成建模,对模型施加正确的载荷,就能进行系统总体变形下的强度校核计算,并对齿轮进行优化设计分析。
但是,MASTA对于复杂几何框架、轴等模型的建立有一定的局限性,只能通过建立中心对称轴的方式代替复杂几何模型[6],这样必然影响复杂几何模型的刚度、强度,进而影响最终结果的准确性。
运用MASTA建立的行星传动机构原始模型如图2、图3所示:
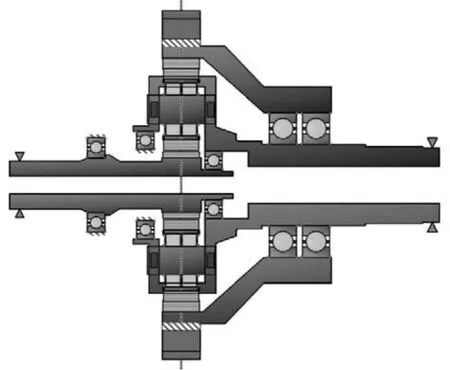
图2 行星机构二维MASTA模型

图3 行星机构三维MASTA模型
3.2 刚度矩阵的求解
由于行星架的结构比较复杂,因而采用Pro/E软件建造三维实体模型。考虑到计算分析的需要,对实体作了诸多的几何清理,例如去除小圆角、小倒角以及不影响结构的小圆孔等,处理后的模型如图4所示:

图4 几何清理后的行星架三维模型
将模型导入有限元软件后,提取行星架刚度矩阵和节点位置信息的分析步骤如图5所示。
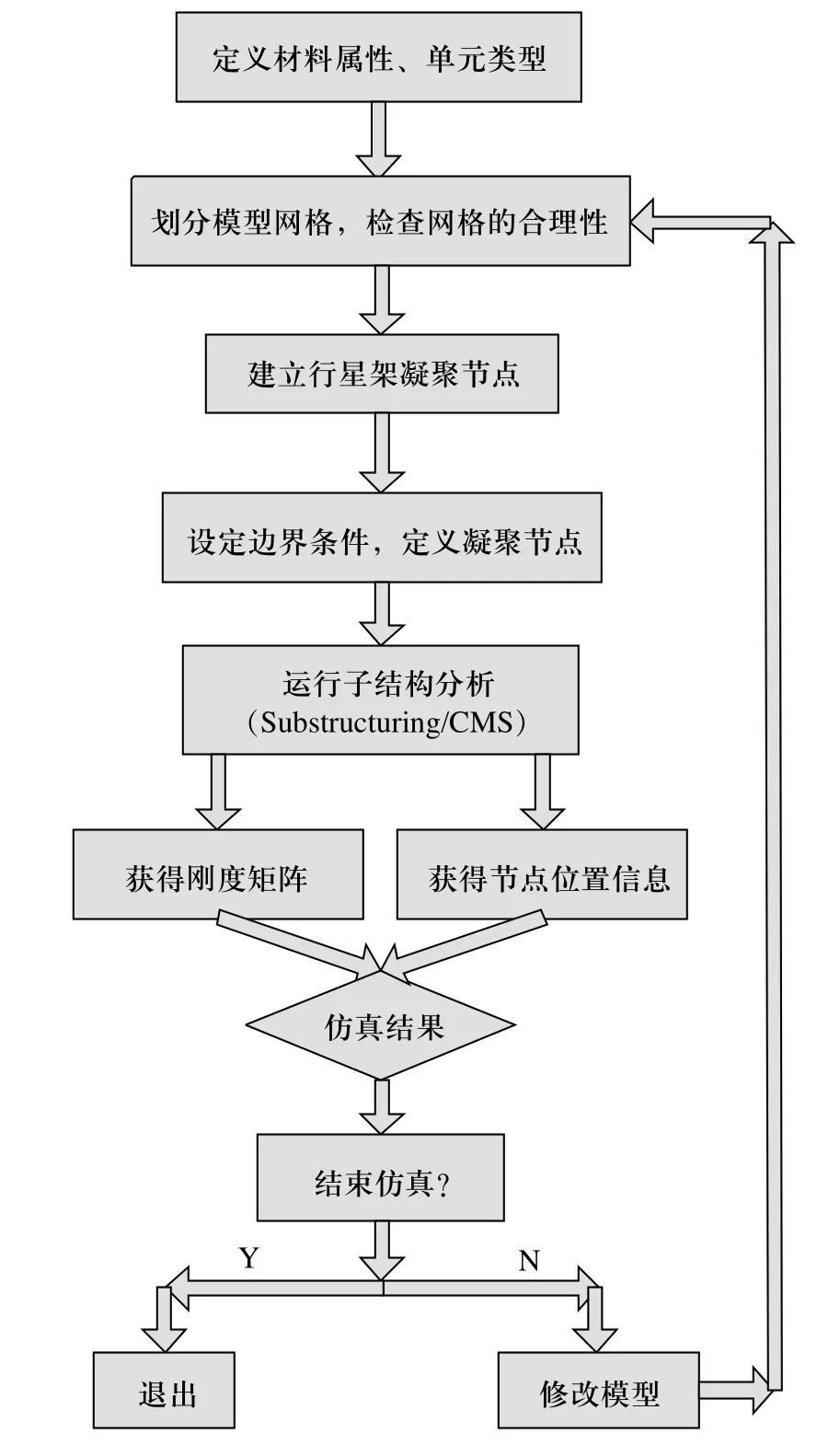
图5 ANSYS提取行星架刚度矩阵和节点位置信息分析步骤
行星架的材料为38CrSi,定义其弹性模量为2.07GPa,泊松比为0.27。单元类型采用Solid-Tet 10node187,网格采用自由划分的方式,行星架与外部构件联结处网格须进一步细化,如图6所示。

图6 行星架有限元网格划分
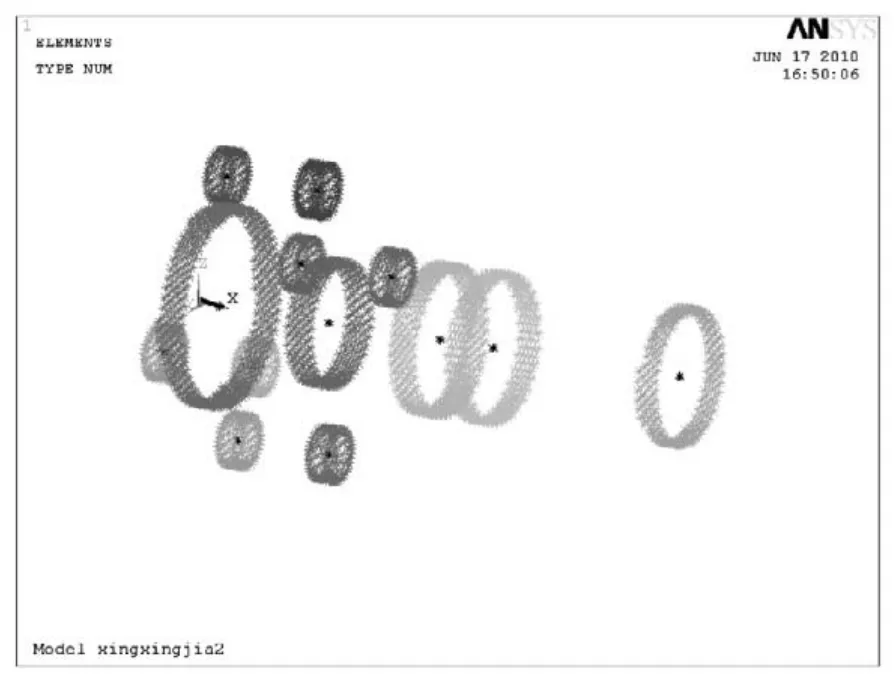
图7 凝聚节点
在ANSYS中,对于整个刚性单元,力/动量或旋转/位移均可由“Pilot节点”描述。如果定义“Pilot节点”,ANSYS仅在“Pilot节点”上检查边界条件,忽略其他节点的任何约束。“Pilot节点”可以是目标单元的一个节点或任意位置的一个节点,仅当旋转或动量加载要求时“Pilot节点”的位置才是重要的。用一个节点的运动控制整个目标面的运动,称该节点为凝聚节点[7]。根据行星传动机构的MASTA系统模型,设定行星架与其他构件相联系的十三个凝聚节点:四个轴承凝聚节点,一个输出转矩凝聚节点,八个行星轴内孔表面的凝聚节点,如图7所示。定义并固定十三个凝聚节点,运用子结构分析法(Substructuring/CMS)提取行星架刚度矩阵和节点位置信息。
3.3 MASTA结果分析
将行星架三维模型(.wrl文件)以及在ANSYS中提取的刚度矩阵、节点位置信息导入行星传动机构的MASTA模型,并且建立相应的联结,得到的MASTA模型如图8、图9所示。
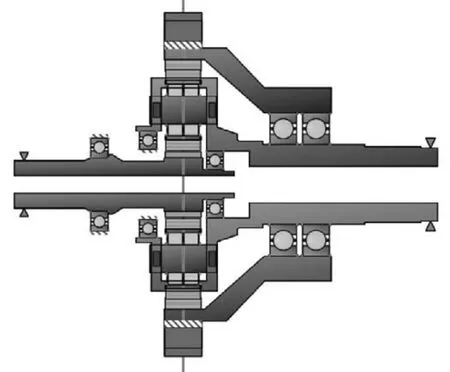
图8 柔性模块二维MASTA模型

图9 柔性模块三维MASTA模型
运行MASTA,进入系统变形模块,得到行星架实际刚度对行星机构齿轮的安全系数和损伤率影响的报告,对比之前的分析结果如表3所示。
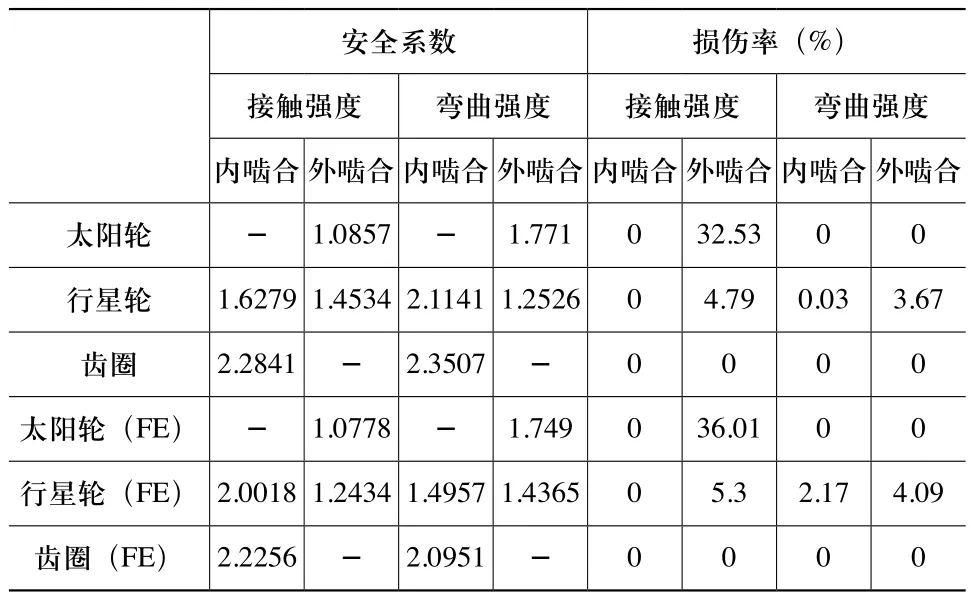
表3 安全系数和损伤率
显然,从以上结果可以直观的看出:行星架实际刚度对计算结果的合理性有着直接的影响(安全系数最大误差发生在内啮合中行星轮的弯曲强度,误差率约为41.3%),因此,运用MASTA柔性模块在分析过程中有着非常重要的作用。
3.4 行星架的有限元分析
进入MASTA的系统变形分析模块,可以得到行星传动机构的系统变形分析结果,并计算出各工况下行星架凝聚节点的受力报告和位移报告,将节点位移报告作为行星架的边界条件,导入有限元软件,采用位移法对行星架进行静力分析,就可得到行星架在各挡位下的应力分布云图和位移云图,如图10、11所示。
行星架材料服从von Mises屈服准则,在各挡下的最大综合应力(von Mises stress)和最大位移(Displacement vector sum)见表4。
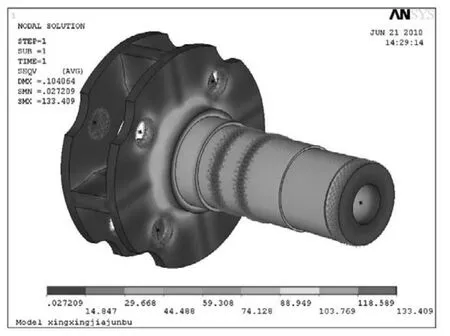
图10 综合应力云图(MPa)
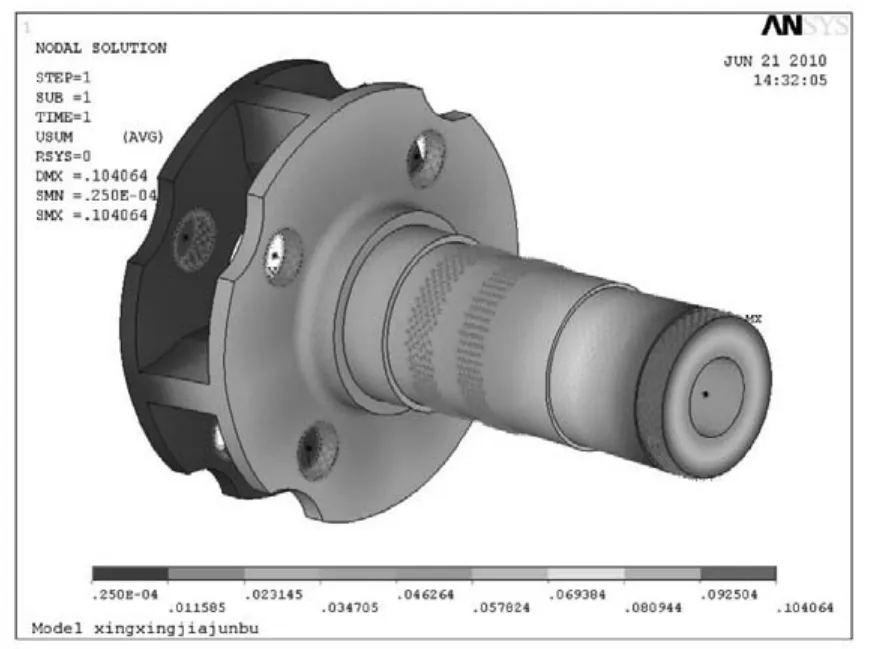
图11 变形云图(mm)
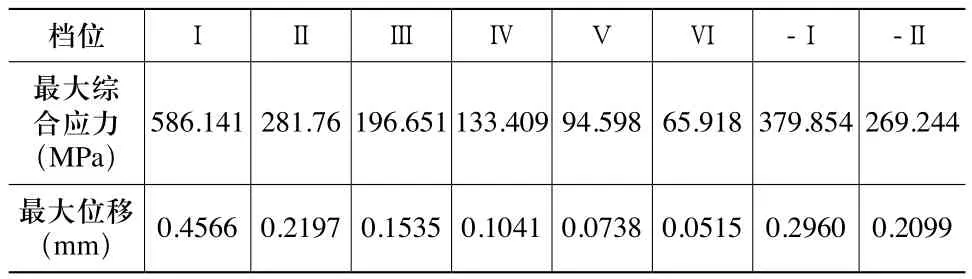
表4 各挡最大综合应力和位移
从综合应力云图可以看出,行星架整体受载比较均匀,最大应力发生在行星架轴颈离输出端最近的轴肩处,Ⅰ挡综合应力最大,峰值达到586.141MPa。经查阅资料[8],38CrSi的材料力学性能:屈服极限σs=835MPa,强度极限σb=980MPa。综合应力峰值距材料屈服极限较远(安全系数约为1.42),况且由表2可知,Ⅰ挡的工作时间较短(仅占总工作时间的2%),因此,可以断定行星架结构满足静强度要求的。
4 结论
在行星机构的传统设计中,齿轮的强度校核完全忽略行星架的刚度变形所造成的齿向偏载,仅应用齿向载荷系数对结果进行修正,缺乏具体的数据支撑,并且,在行星架的有限元分析中,边界条件也没有考虑齿轮偏载对行星架的反作用。本文通过专业设计软件MASTA与有限元软件ANSYS的无缝联结,阐述了行星传动机构的MASTA柔性模块分析流程,既完成了对行星轮系的齿轮强度校核,又实现了行星架的有限元分析。并通过实例验证了该方法的优越性和可行性,其意义主要体现在以下三个方面:
1)清晰的看出行星架刚度对系统变形和强度的影响程度;
2)为行星架的有限元分析提够了准确的边界条件;
3)通过行星架的有限元分析,可以进一步实现对行星架的优化设计。
[1]舒瑞龙. 基于ANSYS的行星齿轮传动设计分析[D]. 贵州大学, 2007.
[2]渐开线齿轮行星传动的设计与制造编委会. 渐开线齿轮行星传动的设计与制造[M]. 北京: 机械工业出版社.2002.
[3]闫清东, 等. 坦克构造与设计[M]. 北京: 北京理工大学出版社, 2007.
[4]蒋友谅. 有限元法基础[M]. 北京: 国防工业出版社,1980.
[5]马少坤, 等. 子结构分析的基本原理和ANSYS软件的子结构分析方法[J]. 广西大学学报, 2004.
[6]程燕, 等. 履带车辆变速机构行星排框架优化仿真分析[J]. 车辆与动力技术, 2008.
[7]刘晖. 基于参数化的齿轮传动接触有限元分析[D]. 大连理工大学, 2002.
[8]成大先. 机械设计手册(第1卷)[M]. 北京: 化学工业出版社, 2002.
