短期化学腐蚀作用下混凝土表面物理性能的变化

王长荣

(1 酒泉职业技术学院建筑工程系，甘肃 酒泉 735000)

在研究混凝土表层物理性能的方法中，回弹法和表层渗透性能测定法已得到了广泛的应用，但是这些应用都有一定的缺陷：回弹法只能应用于普通强度等级的混凝土，并且由于误差太大，只能对混凝土进行定性的判定；表层渗透法容易受混凝土密实程度、环境温度湿度的影响，其应用都有一定的局限。在评判材料表面物理性能的研究方法中，冲击球压法以便于操作、解析理论精确等特点备受重视，目前已成功应用于脆性材料及金属材料的弹塑性变性特征等领域[3-5]，但是在混凝土工程中的应用屈指可数：文献[6]利用冲击球压方法和恢复系数的物理意义研究了喷射混凝土的喷射成功概率；文献[7]利用冲击球压方法，结合等效冲击[8]的概念研究了混凝土材料在小能量冲击作用下的损伤破坏现象；文献[9]研究了混凝土在颗粒冲击作用下局部损伤的机制，但是利用冲击球压技术评价混凝土受腐蚀破坏的研究尚未见报道。本文利用冲击球压方法研究了短期化学腐蚀下混凝土表面的物理性能及变化特征，拟建立一种可快速、敏锐评价混凝土表面受短期腐蚀作用而变化的测试方法。

1 理论背景

假设一个质量为m、弹性模量与泊松比分别为E1 和v1的小球垂直地冲向弹性模量和泊松比分别为E 和v的平面上，接触瞬间小球相对于平面的临界速度为vin，材料受到的最大荷载F 与产生的最大损伤半径a 表示为[10]：

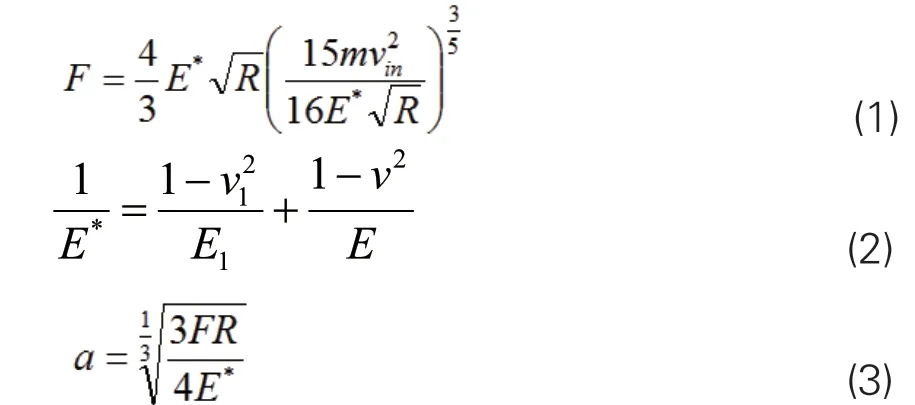
对于任何材料而言理论半径a 永远小于实测半径r，因此符合式(3)关系的情况是不存在的，在实际研究中，往往采用打磨抛光等措施降低二者之间的误差；此外，由于冲击过程中压痕损伤区的复杂变化，r 值在一般情况下略微偏大。假设冲击结束后材料弹性变形完全恢复，残余的损伤区相当于冲击最终产生的损伤。在对材料进行迅速、敏锐地检测时这种假设是可行的。因此损伤区的体积可表示为：

由能量守恒的原理可知，球头接触平面时的动能Uk 在冲击中转化为使材料发生弹塑性变化的变形能UE、UP 和弹性波的振动扩散以及极少量的热能[11]，根据Hutchings[12]的研究，弹性波振动扩散的能量大概占总能量的1%～4%，可以将其忽略不计，因此冲击过程中各组分的能量遵循[13]：

冲击结束后弹性变形能使球头发生速度为vout的回跳[14]，即：

结合式(1-7)，得到动态硬度和恢复系数的表达为

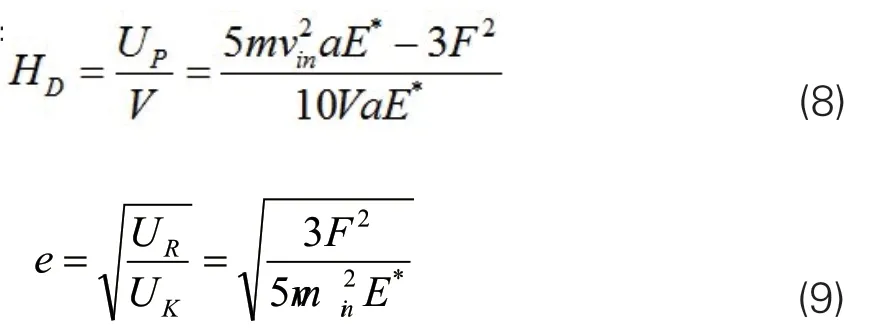
由式(8-9)可知，动态硬度和恢复系数分别定义了一定能量下材料抵抗塑性变形和发生弹性恢复的能力，反映了材料表面弹塑性力学特征。上述公式中出现的物理量除半径r需要测量之外，其他物理量均为已知、或可由传感器读出，因此只要对r 进行精确的测量，就可以方便地评价岩石材料表面的弹塑性力学特征。

2 试验材料与方法

混凝土强度等级为C80，28 天抗压强度为86.2MPa，配合比见表1，采用100mm×100mm×100mm的模具成型。为了保证混凝土强度的顺利发展，拆模后将混凝土置于标准养护室养护56 天，之后分为两组，一组置于标准养护室继续养护，另外一组置于HNO3和5%质量分数的(NH4)2SO4混合溶液中(pH=2.54)，以浸泡3 天105℃干燥1 天为1个循环，3个循环构成1个周期。每个循环结束后测量溶液pH 值并利用HNO3重新将溶液酸度调整至2.54，每个周期结束后对其进行抗压强度和冲击球压试验。

表1 混凝土配合比

冲击球压装置为自己设计，设备原理见图1。其中，球头材料为碳化钨，弹性模量和泊松比分别为600GPa 和0.15，为了降低样品边缘和测点间距所带来的测试影响，对测点位置进行了规范的布置（图2）：测点距样品边缘＞1cm，测点间距＞2cm。冲击过程中的荷载通过传感器精确测定；试验结束后，利用日产VHX-600E 型超景深显微镜对损伤半径进行测量。

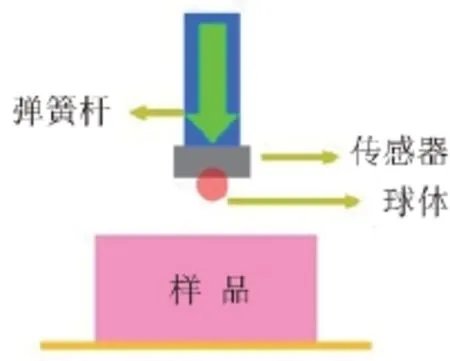
图1 冲击球压装置

图2 测点布置

3 试验结果与讨论

3.1 腐蚀时间对冲击荷载—时间关系的影响

图3 给出了不同腐蚀周期下混凝土在一次冲击荷载作用下冲击荷载与冲击时间的变化曲线。从图中可以看出，随着腐蚀行为的进行，短期内混凝土冲击荷载—时间曲线轮廓没有什么变化，这说明短期的腐蚀不会对混凝土表层以下的结构产生明显的破坏。注意到卸载结束时此关系的变化，可以发现球头并非以0 荷载的形式离开混凝土表面，而是伴随有不同程度的振荡，这种振荡特性随着腐蚀时间的不同而不同；另外，观察荷载峰值也可以发现类似的不同。为了清晰地观察这一现象，现将两区域放大后的曲线关系列于图4、图5。

图3 冲击荷载—时间关系曲线

由图（4-5）可知，随着腐蚀时间的增加，混凝土的峰值变化是较为类似的，而球头所能达到的峰值荷载却是逐渐降低的；应用于本试验中的数据均是在相同高度下落的条件下所记录，因此，混凝土的峰值变化说明了表层腐蚀的存在性和腐蚀时间依赖性。对球头脱离混凝土表面瞬间的冲击荷载——时间曲线分析表明，随着腐蚀行为的进行，卸荷过程中受冲击混凝土区域反作用于球头的冲量也逐渐降低；冲击过程中球头使混凝土局部区域发生弹塑性变形，由于塑性变形基本无法恢复，而弹性变形在卸载过程中基本发生完全恢复，此时产生弹性恢复的能量主要转化为球头离开表面时的冲量；因此腐蚀行为的进行会降低混凝土表面的弹性。

图4 冲击荷载—时间关系(峰值)

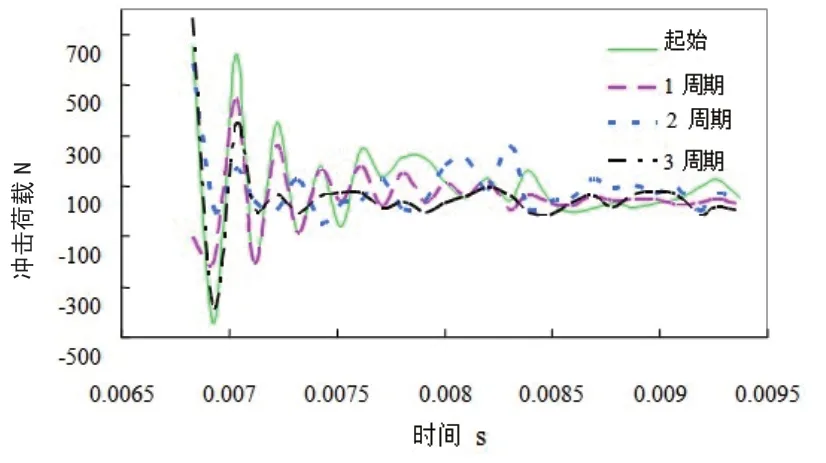
图5 冲击荷载时间关系(卸载)

为了进一步说明这个关系，将冲击荷载—压痕尺寸关系列于图6。从图6 可知，在本试验范围内的混凝土冲击荷载—压痕尺寸关系近似呈现双线性；不论腐蚀时间多长，混凝土总是在度过某一临界荷载后荷载不再随着压痕尺寸的增加而明显增加，但是临界荷载以内的冲击荷载—压痕尺寸斜率却随着腐蚀的进行而降低。这种现象一方面说明了短期腐蚀不会改变混凝土表层以下的物理性能，另一方面追踪到了混凝土表层物理性能随腐蚀的进行而逐渐劣化的现象。

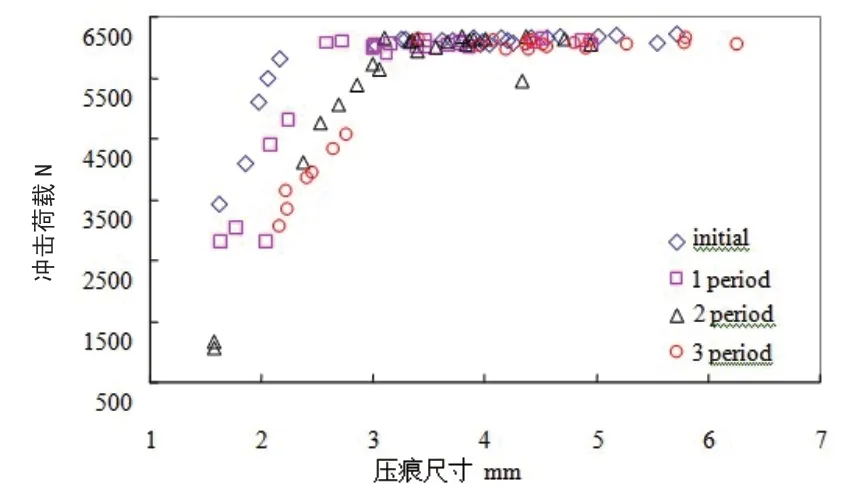
图6 冲击荷载—压痕尺寸关系

3.2 腐蚀时间对溶液pH 值和抗压强度比的影响

随着腐蚀的进行，混凝土的碱性组分不断被溶液中的H+和NH4+所消耗，溶液pH 值远远大于初始值(图7)，从图7 中可以发现，最初的循环结束时溶液pH 值变化最为剧烈，而后的变化基本趋于平衡，这说明了H+和NH4+一开始就造成了混凝土表面组分的大量溶蚀，随着腐蚀的进行，表面组分的溶蚀程度有所降低。

对相同龄期下受腐蚀和标准养护的混凝土抗压强度比进行分析可知(图8)，短期腐蚀不会对混凝土整体性能造成破坏。处于腐蚀溶液中的混凝土短期内表面会受到破坏，而溶液中大量的水份却可以满足混凝土内水泥水化反应的需求，在腐蚀破坏的速率低于水泥水化反应的速率时，抗压强度比不具备精确追踪混凝土腐蚀程度的时效性。

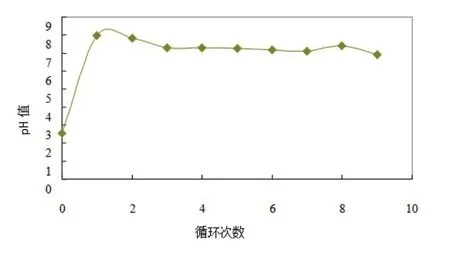
图7 溶液pH 值变化

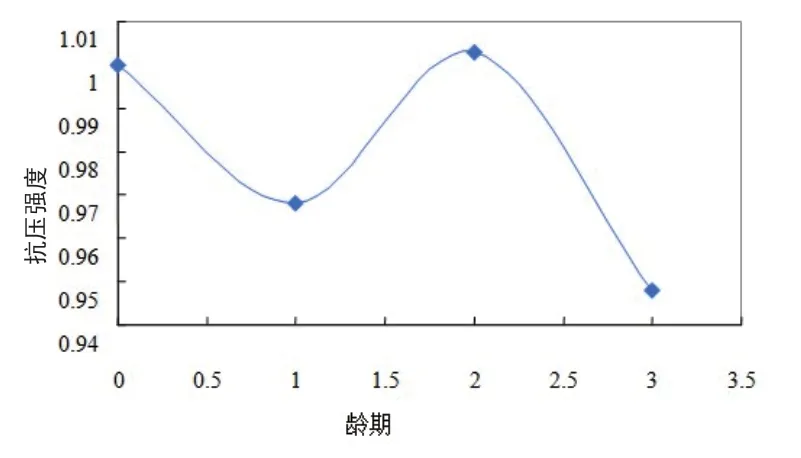
图8 抗压强度比

3.3 腐蚀时间对混凝土表层动态硬度和恢复系数的影响

通过上文的分析可知，宏观物理性能不能准确地表征短期腐蚀下混凝土遭受破坏的程度，而腐蚀溶液pH 值的变化特性只能应用于实验室的连续追踪，在实际情况中，混凝土遭受化学腐蚀破坏并非全部以可见溶液为介质。为此，结合上文所述的公式，在相同荷载水平下得到了不同腐蚀时间下混凝土动态硬度和恢复系数的近似值(图9)。在这里必须要说明的是，动态硬度和恢复系数不是材料固有的参数，它会随着材料的宏观性能、冲击荷载等因素的变化而迅速变化，本文对混凝土动态硬度和恢复系数的定量化是建立在荷载与冲击高度基本相同的前提下。由图9 可知，随着腐蚀的进行，混凝土表层的动态硬度和恢复系数均下降了，且在第二个腐蚀周期之前下降的程度最明显，由于动态硬度和恢复系数分别代表了材料表面在动荷载作用下抵抗局部塑性变形的能力和弹性损耗的特性，因此随着腐蚀的进行，混凝土表面不但抵抗塑性变形的能力减弱了，而且弹性特性也发生了严重的降低。

图9 动态硬度和恢复系数

4 结论

通过对混凝土进行短期腐蚀的试验，可以得到如下结论：

(1)由冲击荷载—时间关系曲线可知，冲击结束后球头离开混凝土表面瞬间所储存的能量随着腐蚀时间的增加而减小；

(2)由冲击荷载—压痕尺寸关系可知，在限定高度的条件下，混凝土冲击荷载—压痕尺寸关系特性表现为双线性，这一特性在短期内不会随着腐蚀的进行而改变，但是在荷载临界值之前曲线的斜率随着腐蚀的进行而逐渐降低；

(3)随着腐蚀的进行，混凝土的动态硬度、恢复系数逐渐降低，并且降低的趋势在腐蚀前期最为剧烈，因此，研究混凝土早期的腐蚀变化对混凝土深层次的腐蚀破坏有重要意义。

(4)抗压强度比不能对短期腐蚀条件下混凝土破坏的程度进行表征，溶液pH 值的变化无法使用于所有混凝土工程，而冲击球压法可以对混凝土短期内的腐蚀破坏程度进行敏感、精确的表征，因此，通过冲击球压法可以方便、快捷地确定出混凝土在腐蚀过程中表面物理性能的变化。

[1]Rendell F,Jauberthie R.The Deterioration of Mortar in Sulphate Environment[J],Construction and Building Materials,1999,13:321～327

[2]Mbessa M,Péra J.Durability of High-strength Concrete in Ammonium Sulfate Solution[J],Cement and Concrete Research,2001,31:1227～1231

[3]Ballout Y,MATHIS J A,Talia J E.Solid Particle Erosion Mechanism in Glass[J],Wear,1996,196:263～269

[4]Amirthan G,Udayakumar A,Bhanu V V,et al.Solid Particle Erosion Studies on Biomorphic Si/SiC Ceramic Composites[J],Wear,2009,doi:10.1016/j.wear.2009.07.007

[5]Nobre J P,Dias A M,Gras R.Resistance of a Ductile Steel Surface to Spherical Normal Impact Indentation:Use of a Pendulum Machine[J],Wear,1997,211:226～236

[6]Armelin H S,Banthia N.Mechanics of Aggregate Rebound in Shotcrete-(Part I)[J],Materials and Structures,1998,31:91～98

[7]陈志城.混凝土材料的接触损伤及球压法无损评价研究[D],中国建筑材料科学研究总院硕士研究生毕 业 论 文，2001：49～51 Chen Z C.Contact Damage and Nondestructive Test of Concrete Materials by Using Sphere Indentation[D],China Building Materials Academy,2001:49～51 (in Chinese)

[8]包亦望，黎晓瑞，金宗哲.等效冲击方法研究硬质颗粒对玻璃的冲击损伤[J]，航空材料学报，1998，2：41～46Bao Y W,Li X R,Jin Z Z.Impact Damage of Glass Evaluated by an Equivalent Impact Method[J],Journal of Aeronautical Materials,1998,6:41～46 (in Chinese)

[9]Momber A W.Damage to Rocks and Cementitious Materials from Solid Impact[J],Rock Mechanics and Rock Engineering,2004,37,1:57～82

[10]Iyer K A.Relationships Between Multiaxial Stress States and Internal Fracture Patterns in Sphere-impacted Silion Carbide[J],International Journal of Fracture,2007,146:1～18

[11]Gilardi G,Sharf I.Literature Survey of Contact Dynamics Modelling[J],Mechanism and Machine Theory,2002,37:1213～1239

[12]Hutchings I M.Energy Absorbed by Elastic Waves During Plastic Impact[J],Journal of Physics D:Apply Physics,1979,12:1819～1824

[13]Kohlhöfer W,PennyR K.Dynamic Hardness Testing of Metals[J],Int.J.Pres.Ves.&Piping,1995,61:65～75

[14]Hussainova I,Kübarsepp J,Shcheglov I.Investigation of Impact of Solid Particles Against Hardmetal and Cermet Targets[J],Tribology,1999,32:337～344