立体图形课件制作中的数学分析与技术手段
2011-08-25430062湖北大学数学与计算机科学学院
430062 湖北大学数学与计算机科学学院 朱 慧
430070 湖北省实验幼儿师范学校 刘 欣
立体图形课件制作中的数学分析与技术手段
430062 湖北大学数学与计算机科学学院 朱 慧
430070 湖北省实验幼儿师范学校 刘 欣
人们很早就认识到图形语言具有特殊作用,从不同的角度、不同的方向观看图形时就会产生不同的视觉效果,图形也就有了文字所不能及的优越性.俗话说得好:“灵感产生于多维度的观察与思考.”初中时期,学生们就曾遨游在三视图的空间里,从正面、侧面和俯视面三个维度观察图形,全面地认识事物,在认知的过程中培养和发展了的空间想象能力.
利用现代信息技术,例如几何画板,鲜活地呈现视图的过程,则更有助于激发学生的学习兴趣,提高教学效果,有步骤地培养学生的空间想象能力.本文仅就三视图课件中正四棱锥的制作来说明如何利用几何画板软件中的【动画】和【移动】命令制作动态旋转的正四棱锥和它的三种视图动画,以及制作过程中的数学思考与技术手段.
【动画】是运动形式,有两种呈现方式:手动动画和自动动画.自动动画又可以分为有规则的运动和无规则的运动(俗称“乱动”).对于无规则的运动,我们不研究它,而其他两种,几何画板都可以满足我们的需求.
几何画板软件中的【动画】和【移动】命令是在【编辑】菜单下的【操作类按钮】中,通过【动画】和【移动】命令制作出具有“动画”功能的按钮,再通过这个按钮对移动对象进行操作和控制.例如,当我们在工作区中选中圆上的点A,再点击【编辑】/【操作类按钮】/【动画】,打开【动画属性】对话框,根据需要选择适当的方向、次数和速度,单击【确定】后,在工作区中生成一个【动画点】按钮(如图1).单击该按钮时,点A在圆上运动.再单击停止运动.
例 制作正四棱锥的三视图的动画.
本课件制作的意图就是将正四棱锥以空间形式动态地展示出各个面,并多角度的观察图形,用动画演变得到正视图、左视图、俯视图(如图2).
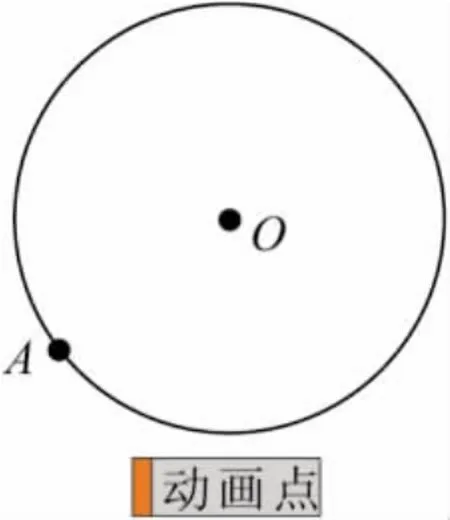
图1

图2 正四棱锥的三视图
在作图之前先了解一下基本信息:
(1)正四棱锥有五个面:四个侧面和一个底面,四个侧面都是等腰三角形,底面是一个正方形,并且正方形的四个顶点共圆.在画法几何中,将立体图形平面化,底面正方形的四个顶点是在某一椭圆上,正四棱锥的顶点在过底面正方形的中心且垂直于底面的直线上.
(2)制作动画要确定动画的对象、动画对象的运动轨迹.
(在具体做动画前必须先画出正四棱锥,画法步骤详见后面附录)
1 转动的正四棱锥(自动动画)
分析 如图3,目前呈现在前面的是△SAB,想要将其他面的三角形依次在正前方出现,显然点S是不动的,只需将底面的四个顶点旋转相应的角度,并且旋转过程中,点与点之间的位置关系不变,均是绕着直线SO转动的,那么它们之间应相互关联.如何关联?四个顶点是由点Q经过迭代得来的,因此四个顶点是受点Q牵制的.可以以点O为旋转中心将点Q绕逆时针方向沿着圆旋转360°(或大于360°),则四棱锥所有面就依次在正前方呈现.动画的对象就是点Q,动画的轨迹就是圆O.但这里的旋转只是将正四棱锥绕底面旋转,如同将四棱锥放在平面上旋转,美中不足的是底面不能转过来.如何才能转动底面呢?再来看图3,转动底面,即是转动底面的椭圆,在作椭圆过程中,点P是任取的点,由它才有了直线PO和之后的一系列动作,因此点P是最原始的关键点,可以转动点P使整个四棱锥包括椭圆在空间内运动.
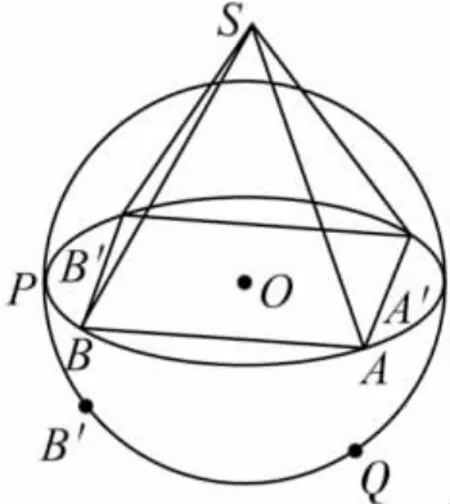
图3
具体的作法如下:
随着网络信息技术的普及,学术期刊的发展环境迎来了极大的变化与挑战。作为分享科研信息和学术交流的阵地,科技期刊的生存方式也发生了根本性的变化。新媒体的出现,多种多样的传播方式使得科研成果的生产加工和转化发生了改变。虽然是科技期刊,应该走在科技前端,但由于期刊品牌在市场上没有知名度和影响力,在收发稿件上很落后,作者和审稿专家队伍也很难扩大范围。对于很多互联网同步不及时的地方科技期刊,期刊品牌影响力不够,知名度也小,许多优秀稿件无处可投,同时稿件的外审工作繁杂,这显然阻碍了科研成果的展示和交流。
(1)作出正四棱锥,如图5所示.(可以将△SAB填充颜色,试图效果更直观)
(2)制作动画按钮【水平转动】.选中点Q,点击【编辑】菜单中的【操作类按钮】/【动画】,在弹出的对话框中选择适当的方向、次数和速度,按【确定】即可在画布上出现【动画点】按钮.右键单击【动画点】/【属性】/【标签】,将“动画点”名称改为“水平转动”.单击【水平转动】,正四棱锥随着点Q的运动而以直线SO为轴在平面内旋转,再点击则停止旋转.
(3)制作动画按钮【底面翻转】.选中点P,操作同上.右键单击【动画点】/【属性】/【标签】,将“动画点”名称改为“底面翻转”.单击【底面翻转】,正四棱锥随着点P的运动而在空间内旋转,再点击则停止旋转.
2 主视图(手动动画)
分析 主视图是从正面内得到由前向后观察物体的视图,特点是正四棱锥的顶点位置不变,底面的中心也不变,只是底面正方形在正视图中缩成一条等边长的水平线段.
易知使底面正方形缩成一条线段,则相应的椭圆也成为一条线段,点Q,A,A'三点重合,故可以以点A为动画对象,使点A移动到点A'即可.
作法 选中点A不放,将点A移动到点A',得到如图4,此时就是该四棱锥的正视图,再点击画布上的【水平转动】按钮,则正四棱锥水平放置的各种形式的正视图都可以呈现出来.例如以上图5的正视图为图6.
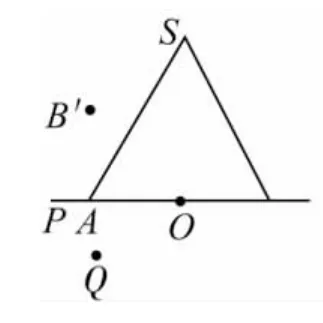
图4
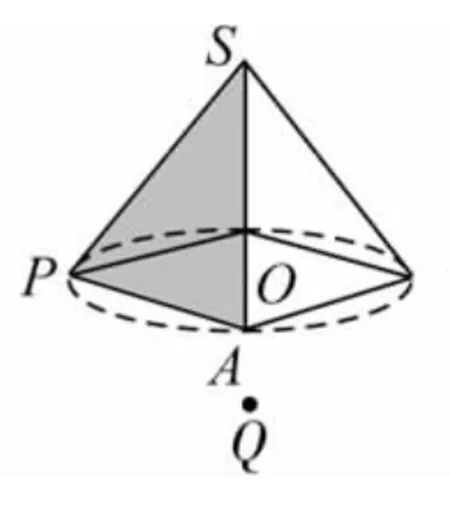
图5
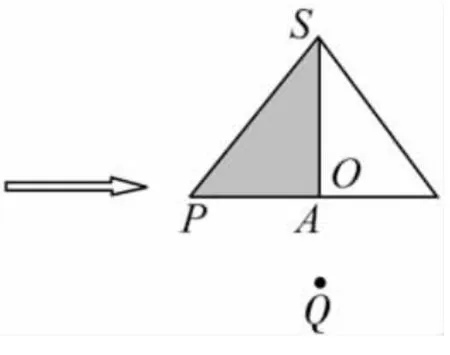
图6
(值得一提的是,在点A旋转过程中,底面其他三点要跟着点A一起运动,就必须与点A相关,这正是通过【迭代】得到正四棱锥的原因.)
3 左视图
分析 左视图是在侧面内由左向右观察物体得到的视图.相当于人以点O为圆心顺时针转90°观察图形,但实际作图时不可能人转,可以换个主体,也就是人不动,将图形以点O为圆心,逆时针转90°,此时的“主视图”便是真正的左视图.
作法同主视图,这里不再详说了.
4 俯视图(移动)
分析 俯视图是在水平面得到由上向下观察物体的视图.它的特点之一是定点S和椭圆中心O重合了,即四棱锥的高退化为0;特点之二是从上往下看底面是内接于圆的正方形.因此动画分为两个过程,一个是定点S退化到圆心O,另一个过程是正方形的一顶点A运动到圆上点Q(伸缩比为1).
作法
(3)合并按钮.以上两个动作可以同时进行,选中按钮【移动A→Q】和按钮【移动 S→O】,点击【编辑】/【操作类按钮】/【系列】,在弹出的对话框中改变标签为“俯视”,选择“同时执行”,“末动作停止”,隐藏按钮【移动A→Q】和【移动S→O】.单击按钮【俯视】,即可得到正四棱锥的俯视图(如图7)
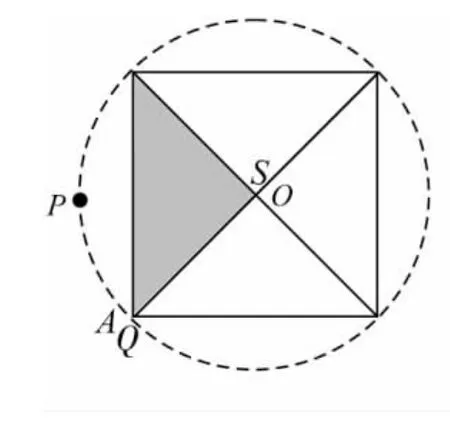
图7
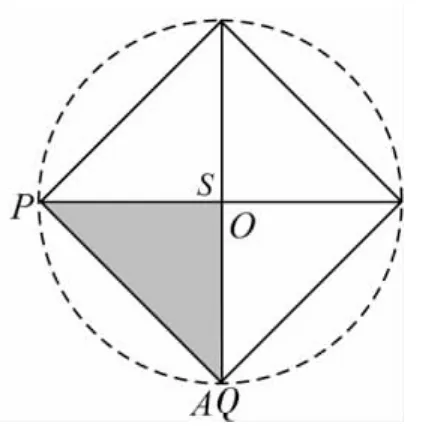
图8
再点击画布上的【平动旋转】按钮,则正四棱锥水平放置的各种形式的俯视图都可以呈现出来.例如以上图5的俯视图为图8.
其他图形如正五棱锥、正六棱锥等通过改变参数n的取值即可得到,而圆柱,直棱柱、球、立方体的三视图都可以类似地作出来.
附录:画正四棱锥
作法 建立一个新的几何画板文件,进行如下操作
(1)作一个圆O,在圆上任取一点 P,选中点P,点O,点击【构造】/【直线】,即得到直线 PO.
(2)制作椭圆.在圆上任取一点Q,选中点Q和直线PO,点击【构造】/【垂线】,点击两直线交点 A'(立即在【显示】菜单中【隐藏垂线】),即过Q作直线PO的垂线交点 A'.连接 QA',在 QA'上任取一点 A,选中点 A,Q,依次点击【构造】/【轨迹】,即得到椭圆.
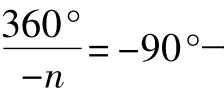
20111118)
