也谈反比例函数中的不变性问题
2011-08-25430030湖北省武汉市华中科技大学同济附中王凯旋
中学数学杂志 2011年24期
430030 湖北省武汉市华中科技大学同济附中 李 鑫 王凯旋
也谈反比例函数中的不变性问题
430030 湖北省武汉市华中科技大学同济附中 李 鑫 王凯旋
文[1]提出反比例函数中的几个不变性问题,笔者最近也在思考反比例函数的一些性质,受此篇文章的影响,结合自己的所思,对文[1]提出的问题进行了更一般性的总结.
1 坐标乘积不变性(反比例函数的基本不变性)
2 面积不变性
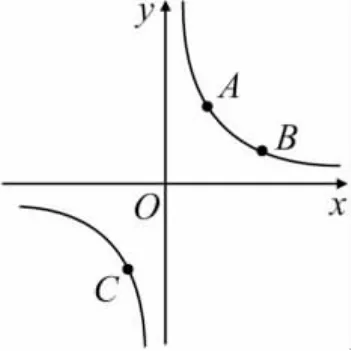
图1
例2 如图 2,若 A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=(k为常数,且k≠0)的图象上,由坐标乘积不变性可得:SAA1OA2
点评 坐标乘积不变性和面积不变性可分别看作反比例函数的代数不变性和几何不变性,它们反映了双曲线的代数与几何的统一性.也是双曲线的核心性质.
3 定比平分不变性
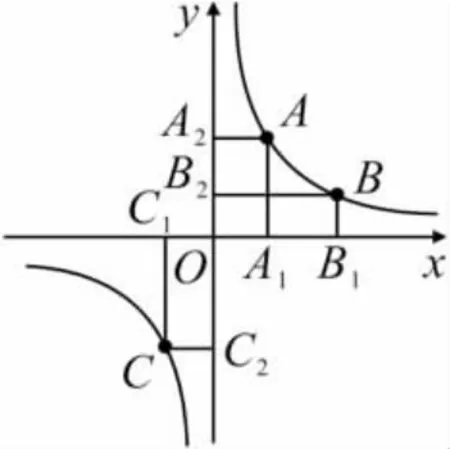
图2


图3
证明 设 B(a,b),则 BC=a,AB=b,
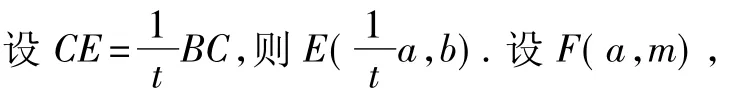

即E点是BC的t等分点时,F点是AB的t等分点.特别地,当E点是BC的中点时,F是AB的中点.
4 位置不变性
证明 如图4,设点A的坐标为(x1,y1),点 B 的坐标为(x2,y2),
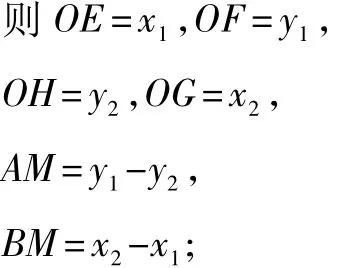

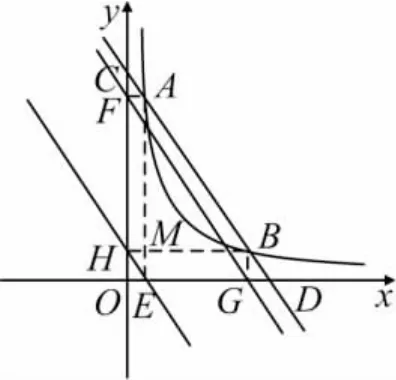
图4
点评 如图5,当点A,B在双曲线的两支上时,结论依然成立,证明方法相同.
5 线段长度不变性
证明 (1)如图4,由位置不变性知HE∥AB,则四边形HEDB和四边形HEAC是平行四边形.
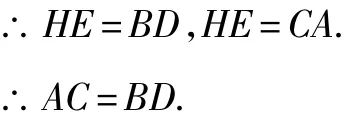
(2)如图5,由位置不变性知HE∥AB,则四边形CEHB和四边形AEHD是平行四边形.
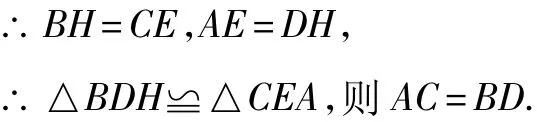
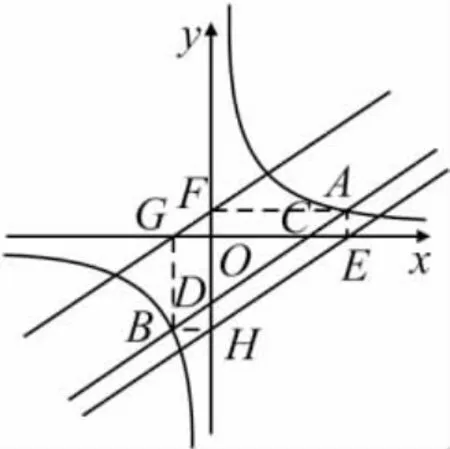
图5
6 乘积不变性
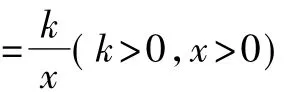
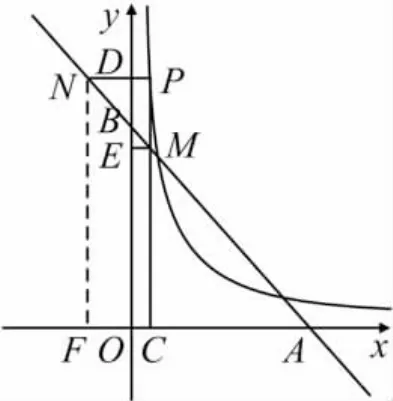
图6
证明 过点M,N分别作ME⊥y轴于E,NF⊥x轴于F.
设点P的坐标为P(x1,y1),

1 郭海军.例谈反比例函数中的几个不变性问题[J].中学数学(下半月)2009.6
20111201)
