标新立异的三角形创新题
2011-08-25312050浙江省绍兴县平水镇中黄绍军沈岳夫
312050 浙江省绍兴县平水镇中 黄绍军 沈岳夫
标新立异的三角形创新题
312050 浙江省绍兴县平水镇中 黄绍军 沈岳夫
创新型试题是考查学生数学能力的最好题型之一,它既能考查学生适应新问题、接受新知识、认识新事物的能力,又能考查学生的自学能力,信息的收集、迁移和应用能力.此类题型新颖别致,颇具魅力,已成为中考试题中的一朵奇葩,其中对新概念信息的提取和化归转化是求解的关键,也是一个难点.本文拟从2011年中考试题中,采撷几束三角形创新型试题加以分类解析,与读者共享.
1 理解概念,深度新应用
例1 (2011年宁波市)阅读下面的情景对话,然后解答问题:
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在 Rt△ABC 中,∠ACB=90°,AB=c,AC=b,BC=a,且 b>a,若 Rt△ABC 是奇异三角形,求 a ∶b ∶c;
(3)如图1,AB是⊙O的直径,C是⊙O上一点(不与点 A,B 重合),D 是半圆)ADB的中点,C,D在直径AB的两侧,若在⊙O内存在点 E,使得 AE=AD,CB=CE.
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
简解 (1)真命题.

图1

点评 此题呈现了新概念——“奇异三角形”.先是要求学生通过阅读,理解对话的核心内容,再运用所学知识解决类似的相关问题.第(1)小题考查学生对新概念的认识,在简单运用中加深了对概念特征的理解;第(2),(3)两小题在学生理解的基础上进行不同情境的运用,让考生在新情境中对信息进行加工,培养了学生对信息理解、加工和利用信息的能力.同时,第(2)小题的研究又为第(3)小题的探究做了很好的铺垫;第(3)小题又考查了分类的思想,让对学生的考查又上了一个台阶.此类试题除了考查学生的阅读理解能力以外,还考查合理猜想、推理判断的能力以及分类讨论思想的运用.
2 作图验证,实践新知识
例2 (2011年南京)如图2,P为△ABC内一点,连接 PA,PB,PC,在△PAB,△PBC 和△PAC 中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
(1)如图3,已知 Rt△ABC 中,∠ABC=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,试说明E是△ABC的自相似点.
(2)在△ABC 中,∠A<∠B<∠C.
①如图4,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.
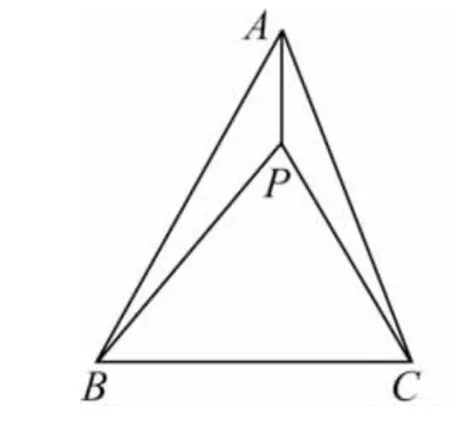
图2
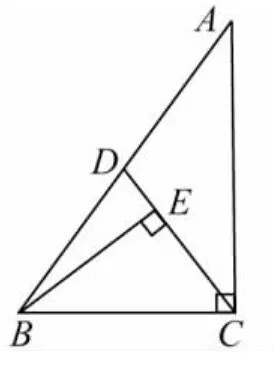
图3
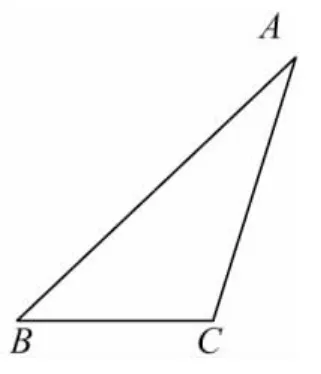
图4
简解 (1)根据题意易证∠BCE=∠ABC和∠BEC=∠ACB.
所以△BCE∽△ABC.
故E是△ABC的自相似点.
(2)①作图如图5,作法如下
(ⅰ)在∠ABC内,作∠CBD=∠A;
(ⅱ)在∠ACB内,作∠BCE=∠ABC;BD交CE于点P.则P为△ABC的自相似点.


图5
点评 此题难度不大,整个问题呈现出“提出新概念 — →作图验证 — →解决问题 — →新情景下运用方法”的解题思路.要求学生在阅读的基础上准确理解“自相似点”的内含和本质,并能运用旧知识对新概念进行合理的解释,进而将陌生的概念转化为熟悉的知识去理解和解答.此题设计了3个层层递进的问题,可以全面考查学生思维的全过程,既能考查学生对“自相似点”的掌握情况,又能考查学生的知识迁移能力和解决问题的能力,是一种新颖的中考试题考查模式.第(1)小题找准三角形是关键;第(2)小题中的最后一个小题的解题突破口在于灵活运用三角形内心是角平分线的交点和相似三角形对应角相等的性质推出三个角之间的关系,再应用三角形内角和定理求解.
3 动手操作,探究新图形
例3 (2011年宁德)定义:三边长和面积都是整数的三角形称为“整数三角形”.数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图6所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①摆出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
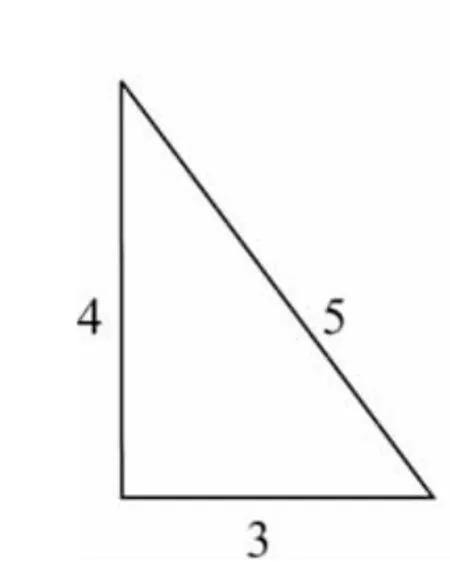
图6
简解 (1)小颖摆出如图7,图8所示的“整数三角形”;小辉摆出如图9所示三个不同的等腰“整数三角形”.
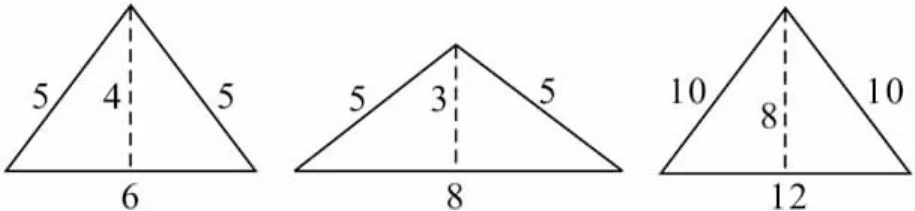
图9
(2)①不能摆出等边“整数三角形”.理由如下:
所以不存在等边“整数三角形”.
②能摆出如图10所示一个非特殊“整数三角形”.
点评 此题定义了“整数三角形”,其实质就是对常见“勾股数”的变式运用,它源于教材、高于教材、活于教材.试题从基础入手,以最常见的直角三角形(勾三股四弦五)为载体,通过模仿(摆直角“整数三角形”)→尝试(摆等腰“整数三角形”)→论证(摆等边“整数三角形”)→拓展(摆非特殊“整数三角形”),在问题设计上层层深入,每一步都为下一步的思维活动打下基础,是一个蕴涵了让学生经历动手操作、猜测验证、合情推理、有条理论证的数学化思维过程,考查了基于数学实验的数学问题形成的一般思路及探究能力,在解决数学问题的过程中培养学生注重基础、拓展思维、变式推理的能力.解答此题的难点在最后一问,要学生通过前面的铺垫受到启发,运用类比思想,归纳发现:两个全等的直角三角形可以拼成一个等腰三角形,由此进一步发现,要拼出一个非特殊“整数三角形”需要两个不全等的直角三角形,同时这两个直角三角形要有一条直角边是相等的.
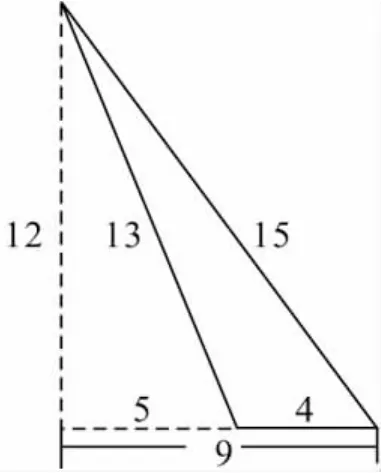
图10
4 通过阅读,诠释新结论
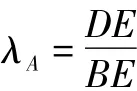
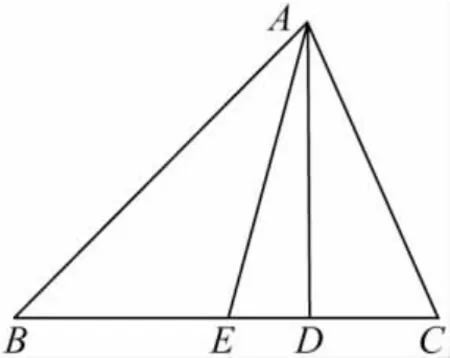
图11
(1)如图12,已知在 Rt△ABC 中,∠A=30°,求 λA,λc;
(2)在每个小正方形边长为1的4×4方格纸上(如图13),画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且λA=2,面积也为2;

图13
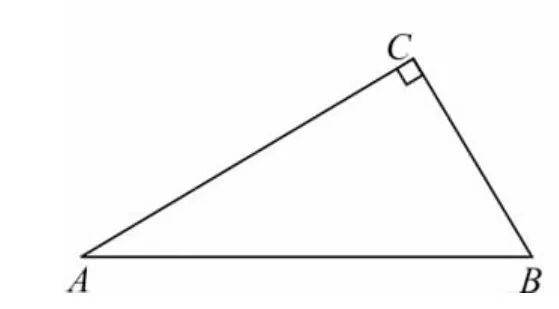
图12
(3)判断下列三个命题的真假.(真命题打√,假命题打×)
①若△ABC中,λA<1,则△ABC为锐角三角形;
②若△ABC中,λA=1,则△ABC为直角三角形;
③若△ABC中,λA>1,则△ABC为锐角三角形;
简解 (1)如图14,作CD⊥AB,垂足为D,
(2)如图15所示.
(3)①×;②√;③√.
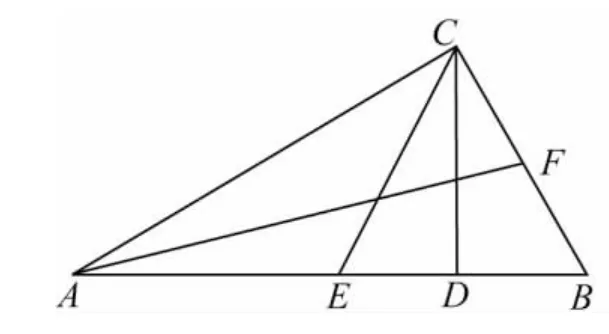
图14
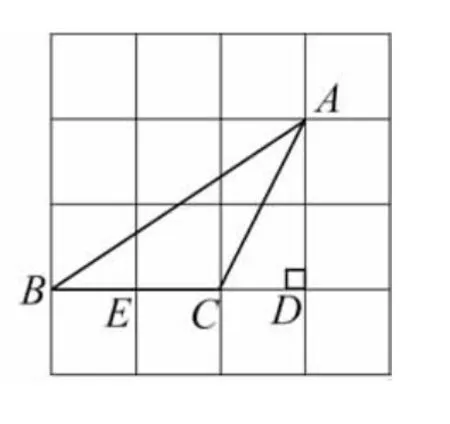
图15
点评 此题是一个新颖的情景题,给学生提供了阅读理解的平台,体现了数学考试的公平性,试题难度也呈梯度上升,集阅读、操作、数学思考于一体,考查学生的阅读理解能力、知识运用能力.其过程就是经历数学化的思维过程.问题的设计由浅入深,层次性强,考查了学生的阅读理解能力和数学迁移能力.充分体现出设计者的独具匠心,不失为一道设计巧妙的亮点试题.试题起点低,从第(1)小题中的求解“λA,λc”;然后提出第(2)个问题;再到第(3)个问题的命题真假判断.给学生指出求解的方向,可以有的放矢,不走冤枉路.让学生在思考中体验知识的形成过程,让学生始终处于“思考—→收获 — →再思考 — →再收获”的这样一种情感体验之中.
5 领悟方法,解决新问题
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且 ED=EC,如图16,试确定线段AE与DB的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图17,确定线段AE与BD的大小关系.请你直接写出结论:
AE________DB(填“>”,“<”或“=”)
(2)特例启发,解答题目
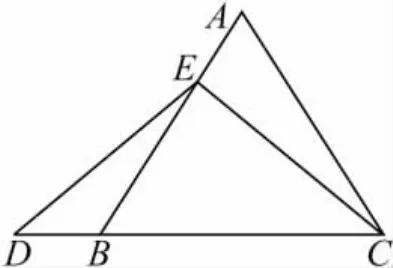
图16
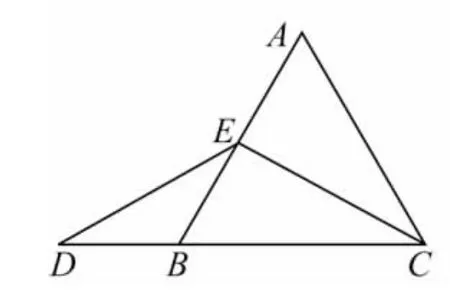
图17
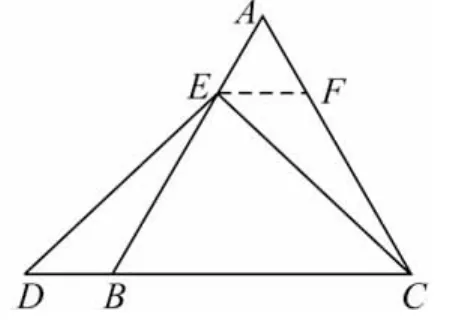
图18
题目中,AE与BD的大小关系是:AE________DB(填“>”,“<”或“=”).
理由如下:如图18,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
简解 (1)由题意,可求得∠D=∠DEB=30°,则能推知DB=BE=AE,故应填“=”.
(2)由(1)知,猜想答案应填“=”.
证明略.
(3)CD的长是1或3.思路如下:
方法1 (构造30°的直角三角形) 当点E在AB的延长线上时,如图19所示,易求CD=DB+BC=2+1=3;当点E在BA的延长线上时,如图20所示,易求CD=2CF=1.
方法2 (构造相似三角形) 可在图19中,分别过点A,点E作CD的垂线,垂足依次为M,N.
同理,在图20中,过点A作CD的垂线,垂足为M,
过点E作CD的垂线,垂足为N,则△ABM∽△EBN,
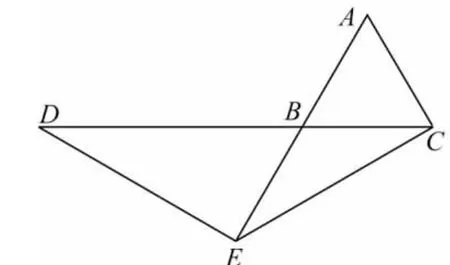
图19
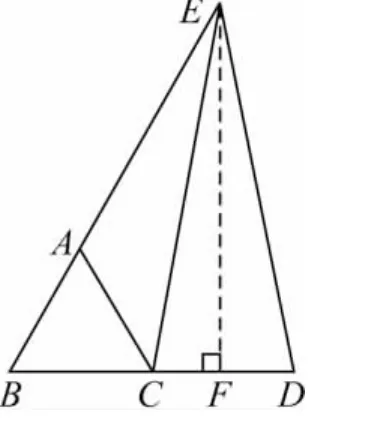
图20
方法3 (直接应用前面的结论) 根据图19,图20,若直接引用第(2)小题的结论“AE=BD”,得出的结果则更快一点.
点评 此题以等边三角形为载体,通过改变条件“点E为AB的中点”→“点E在AB上”→“点E在直线AB上”为手段,在三角形中利用添加辅助线构成全等形,完成从合情推理到演绎推理的转变.主要考查对全等三角形的性质和判定,三角形的内角和定理,等边三角形的性质和判定等知识点的理解和掌握,能综合运用这些性质进行推理是解题的关键.此题以范例的形式给出,并在解决问题的过程中暗示解题思路,要求学生在理解的基础上进行迁移运用,再以活动中获得的数学经验与知识解决新问题.这种采用分层递进的方式探究相关线段间的大小,实现特殊到一般的思想的数学领悟,较好地考查学生的知识迁移能力和解决问题的能力.这类试题突出了对数学本质和思想方法的考查,让学生思维有更广阔发挥的空间和较大选择的自由度,能很好地培养学生的探究精神、创新意识和发散思维.
20111202)
