pH值系统变论域模糊控制器的设计及性能分析

佟世文

(中国天辰工程有限公司，北京 100029)

pH值系统变论域模糊控制器的设计及性能分析

佟世文

(中国天辰工程有限公司，北京 100029)

针对pH值非线性控制系统，设计了一种实时简化变论域模糊控制器.将变论域思想与实时模糊推理策略相结合:一方面论域随着误差的减小而收缩，而论域的收缩相当于控制规则的增加，从而增加了控制精度;另一方面采用实时模糊推理方法，即对于一个二入一出的模糊控制器，一次推理过程中最多只激活4条控制规则，在控制的过程中只考虑这4条控制规则.这2种思想的结合使得控制规则的设计大大简化，可以采用批处理的方式设计控制器，不仅加快了系统的动态响应，也提高了控制精度.仿真结果证实了这种控制方法的有效性.

pH系统;变论域;实时模糊推理;模糊控制器

pH值酸碱中和过程是一个典型的非线性系统，在工业上有着广泛的应用，如电厂、炼油厂的污水处理，集成电路的蚀刻，锅炉供水，制药厂的生化反应等.由于其本身的高度非线性，难以建立精确的线性模型，使得多年来对这一被控对象的研究一直在进行.已有很多成果应用于pH值系统，有改进的PID控制［1］、神经网络控制［2］、模糊控制［3］、变结构控制［4］、预测控制［5］等.这些方法中有的控制效果还有提高的余地，有的算法太复杂，不利于工业应用;有的算法的适应性较差，工艺条件的改变将导致模型误差增大，使控制效果变差.本文将变论域和实时模糊推理策略相结合，设计了一种既简单又好用的实时简化变论域模糊控制器［6］应用于pH值非线性系统的控制中.

1 pH值系统建模

如图1所示的是一个典型的pH值酸碱中和系统CSTR反应器［7］.设碱液的流量为U(t)，浓度为Calkali;酸液的流量为F(t)，浓度为Cacid;酸碱中和后的混合液的流量为P(t).碱液与酸液在CSTR反应器中在搅拌器的作用下充分混合，发生中和反应.通过调节碱液流量U(t)，使混合后的出口液达到要求的pH值.根据质量守恒及酸碱中和原理，可得到如下模型:

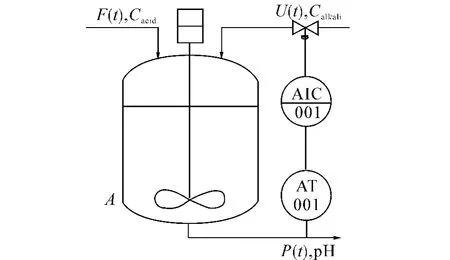
图1 酸碱中和系统CSTR反应器Fig.1 CSTR reactor of an acid-alkali neutralization system

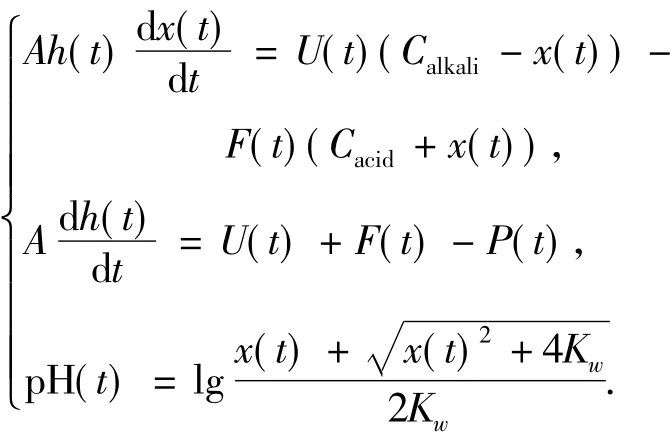
式中:h(t)为液位，m;Calkali为碱液浓度，kmol/m3;Cacid为酸液浓度，kmol/m3;x(t)为氢氧根离子和氢离子浓度之差，kmol/m3;A为反应器的截面积，m2;Kw为水平衡常数.

2 控制难点及控制策略

根据所列方程，对模型进行仿真，可得在中性点pH=7附近的仿真曲线.从图2中可以看出pH值是一个高度非线性的系统，对其进行控制主要有以下难点.

1)采用线性化模型进行控制器设计，在不同的工作点时模型参数相差较大，难以准确描述被控过程［8］，设计出的控制器控制效果不佳.

2)采用其他的非线性方法，设计过程复杂［2］，对系统的软硬件要求较高，不利于在实际中应用.

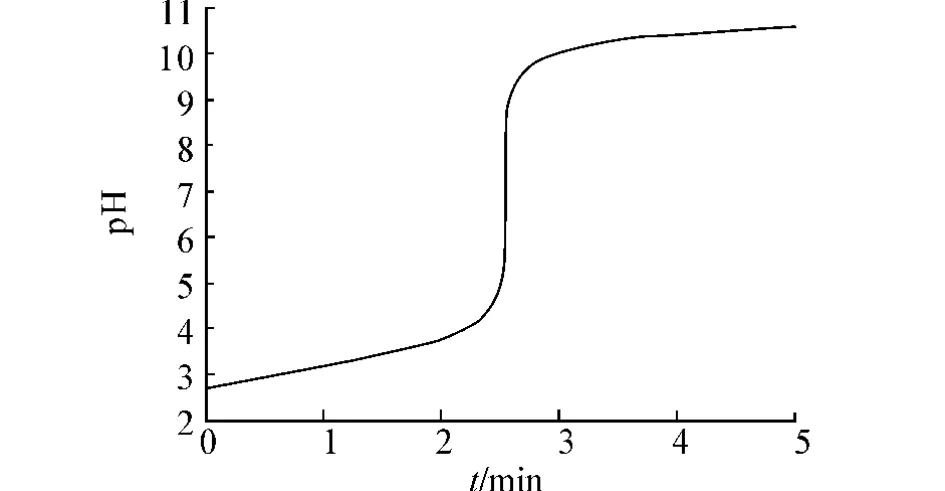
图2 pH值特性曲线Fig.2 pH titration curve

本文采用了一种实时简化变论域模糊控制算法，以pH值为被控变量，以碱液的流量U(t)作为操作变量，以酸液的流量F(t)和混合液的流量P(t)作为扰动变量.在整体上控制结构形式保持不变，但在局部论域会随着误差的变化而伸缩，论域缩小相当于控制规则的增加，在变论域机制下，可根据系统的动态过程设计有限几个关键的控制规则，通过论域的收缩，在关键控制规则之间进行插值，相当于增加了控制规则，从而可以实现较精确的控制.这种控制算法很好地处理了“整体与局部”的关系，提高了控制性能.另外采用了实时推理策略，即对于一个二入一出的模糊控制系统，每次最多只能激活4条控制规则，在动态推理过程中，只需考虑这4条规则，而无需考虑所有的规则，从而可以采用实时动态推理的方式实现控制，控制算法简单.变论域配合实时推理，在控制规则的设置上也可以大大简化，使这种方法非常适合在线精确控制.

3 模糊控制器设计

采用典型的二入一出的控制结构(如图3所示 )，以给定pH值与实际pH值的误差e及误差的变化ec作为输入，以控制作用(碱液的流量U(t))作为输出.Ke、Kec、KΔu分别为误差e、误差的变化ec及增量的控制作用Δu的调节因子.变量e、ec可以通过等式x=Ke·e，y=Kec·ec标准化成x、y.α(x)、β(y)、γ(x，y)是标准化论域X、Y及Z上的伸缩因子，为了使系统在达到稳态时没有误差，需要引用积分作用，因而采用增量算法.

图3 变论域模糊控制结构Fig.3 Structure of the variable domain fuzzy control

设偏差e的语言变量为E，其相应的模糊子集为Ai(i=1，2，3，4，5)，论域为X=［－2，2］，模糊子集的5 个语言值为L(e)=(NB，NS，ZE，PS，PB)，其三角型隶属度函数如图4所示.

设偏差ec的语言变量为EC，其相应的模糊子集为Bj(j=1，2，3，4，5，6，7)，论域为Y=［－2，2］，模糊子集的7 个语言值为L(ec)=(NB，NM，NS，ZE，PS，PM，PB)，其三角型隶属度函数如图5所示.

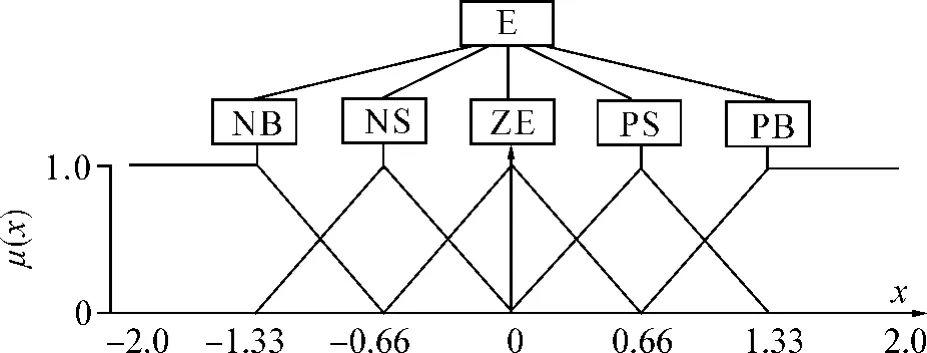
图4 变量e的隶属度函数Fig.4 Membership function of variable e

图5 变量ec的隶属度函数Fig.5 Membership function of variable ec

设输出控制量Δu的语言变量为ΔU，其相应的模糊子集为Cm(m=1，2，3，4，5，6，7)，论域为Z，划分成7个等级Z={ －3，－2，－1，0，+1，+2，+3} ，模糊子集Cm的7 个语言取值为L(Δu)=(NB，NM，NS，ZE，PS，PM，PB)，相应的隶属度如表1所示.

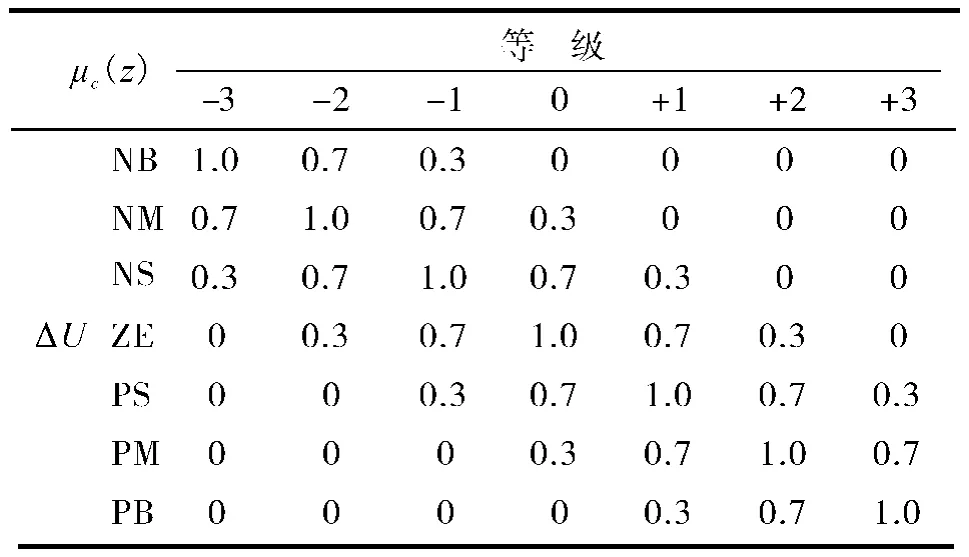
表1 变量Δu随等级变化的隶属度函数Table 1 Membership function of variable Δu

3.1 变论域策略

变论域是通过伸缩因子 α(x)、β(y)、γ(x，y)与标准化论域X、Y、Z相乘作为新的论域来实现的.伸缩因子有多种定义方法，本文采用如下的指数型伸缩因子.

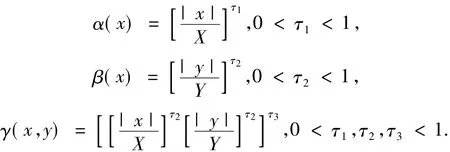
式中:γ(x，y)是标准化的论域Z的伸缩因子，用于调节输出论域的大小，当输入论域随着误差的减小而收缩时，输出论域也应该随之减小，以便使调节过程更加精细.

由于误差e、误差的变化ec是通过调节因子映射到标准化论域X、Y上的，因此有x≤X，y≤Y.再加上 τ1＜1、τ2＜1、τ3＜1，可以得出 α≤1、β≤1、γ≤1.论域会随着偏差的增大和减小而增大和减小，但不会超过标准论域.论域的收缩相当于控制规则的增加，从而既保证了初始论域的设置又提高了控制精度.在这种情况下，专家的经验，区域的划分以及隶属度函数的选择都变得不重要了，只要掌握规则的大致趋势就可以了，因而可以采用较少的控制规则实现较精确的控制［9－10］.

3.2 实时推理策略

由典型的二阶系统动态响应曲线，根据偏差和偏差的变化便可决定相应的控制作用大小，在波峰和波谷处，误差的变化EC为零，如果输出值远小于给定值，即E=PB，这时要使误差减小，需要增大控制作用，可将控制作用输出设置成PB.如果输出值远大于给定值，即E=NB，这时要使误差减小，需要减小控制作用，可将控制作用输出设置成NB.在曲线误差等于零的附近，控制作用的可采用和误差的变化EC相同的.这样，控制规则的设计就变得非常简单，只需分别考虑误差E为零及误差的变化EC为零的点.因而可以得到如表2所示的简化控制规则.

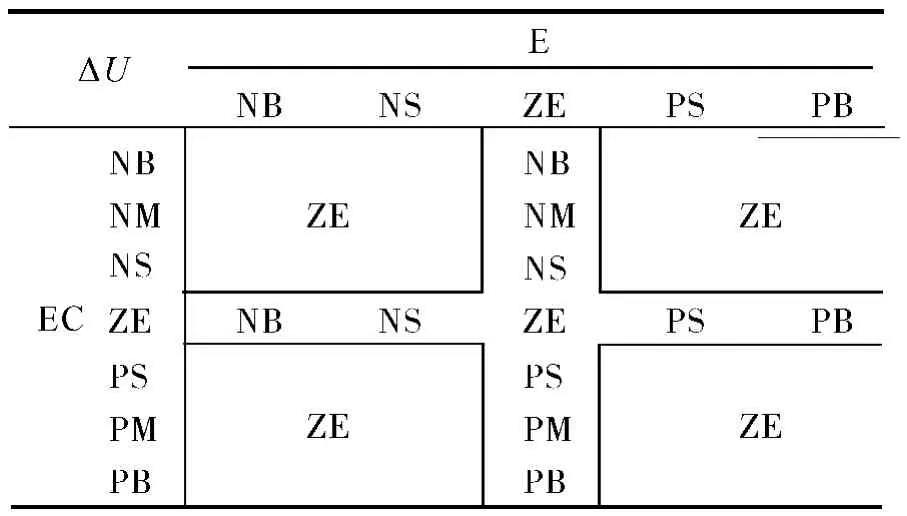
表2 控制规则表Table 2 Map of the control rules

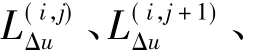
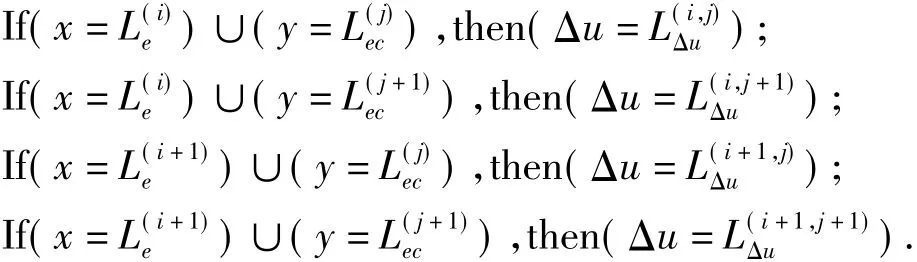
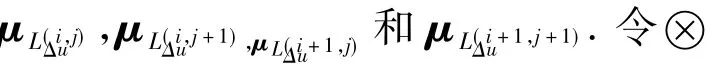
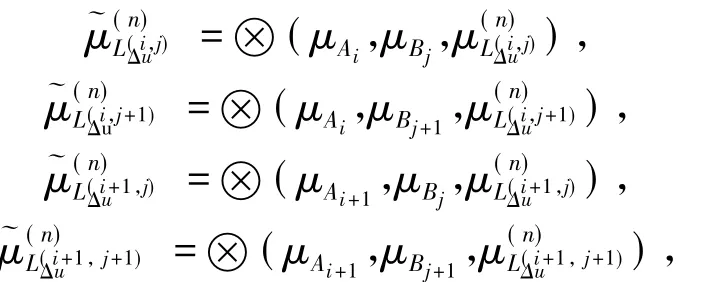
令⊕是最大化算子，计算

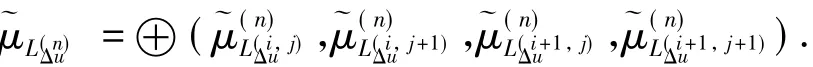
式中:n=1，2，…，7.

标准化的控制输出增量Δu可以采用重心法解模糊

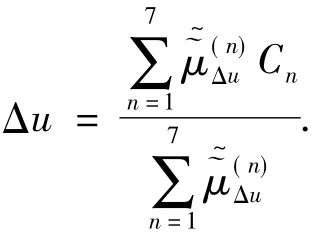
解标准化是通过标准化的输出值Δu乘以调节因子KΔu实现，因此控制作用u(k)可以通过下式计算:

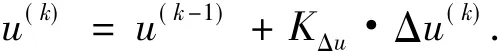
4 控制器的批处理设计

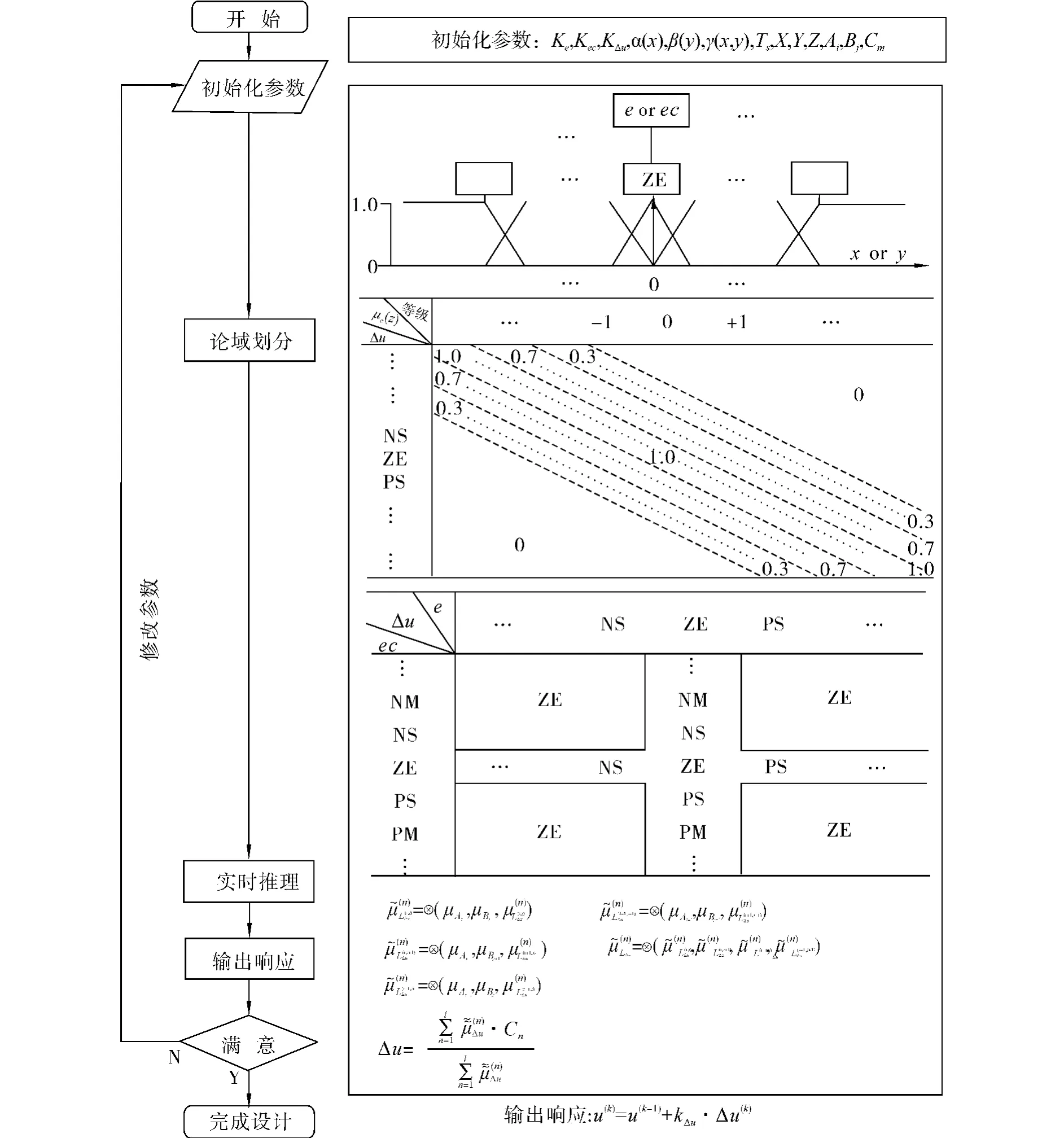
图6 实时简化变论域模糊控制器的批处理设计Fig.6 Batch design method for the real-time simplified variable domain fuzzy controller

变论域配合实时推理，再加上控制规则的设计是根据典型的二阶动态响应过程，具有形式不变性，使得控制器的设计变得非常简单、通用，可以采用批处理的方式进行设计(如图6所示).只需事先设计好伸缩因子 α(x)、β(y)、γ(x，y)，调节因子Ke、Kec、KΔu，输入论域X、Y，输出论域Z，及其模糊子集划分Ai、Bj、Cm，按着图6的流程便可生成一个实时简化变论域模糊控制器，再根据输出的动态响应曲线适当调节这些初始化参数，直到获得满意的结果.换成其他的被控过程，无需再进行具体的论域划分、控制规则设计以及推理设计，只要初始化参数，执行批处理程序便可完成控制器的设计.

5 仿真及性能分析

为验证控制器的性能，在Matlab的Simulink环境下建立pH值系统的C－S函数模型，设F=0.112 m3/min，P=0.224 m3/min，Cacid=0.001 kmol/m3，Calkali=0.001(kmol/m3，A=2 m2，Kw=10－14，初始液位h=4 m.pH的设定值分别取6.5、7.0和7.5，实时简化变论域模糊控制器的参数Ke=0.024 8，Kec=0.001 8，KΔu=0.3，α =0.1，β =0.1，γ =0.01，采样时间0.3 s;普通模糊控制器的参数与实时简化变论域模糊控制器的参数相同，只是论域不随误差的变化而变化;PID控制器的参数为P=0.12，I=0.2，KD=0，进行仿真比较研究，图7是3种控制方法的仿真比较，上部分是pH值输出，下部分是控制器输出，即碱液的流量.

图7 3种控制方法的仿真结果Fig.7 Simulation results of three control methods

从图7中可以看出，采用实时简化变论域模糊控制算法，不仅动态响应大大变快，从PID控制的分钟级提高到秒级，而且稳态精度也大幅提高.而且这种算法的计算量很小，非常适合实时在线应用.为了对3种控制方法进行更清晰的比较，针对pH=7.0的控制曲线，分别对3种方法的e和ec作相平面分析(如图8所示)，从图中可以看出实时简化变论域模糊控制方法较其他2种方法能更快地进入稳态过程且没有偏差.其他2种方法的动态响应较慢，控制效果不太理想.

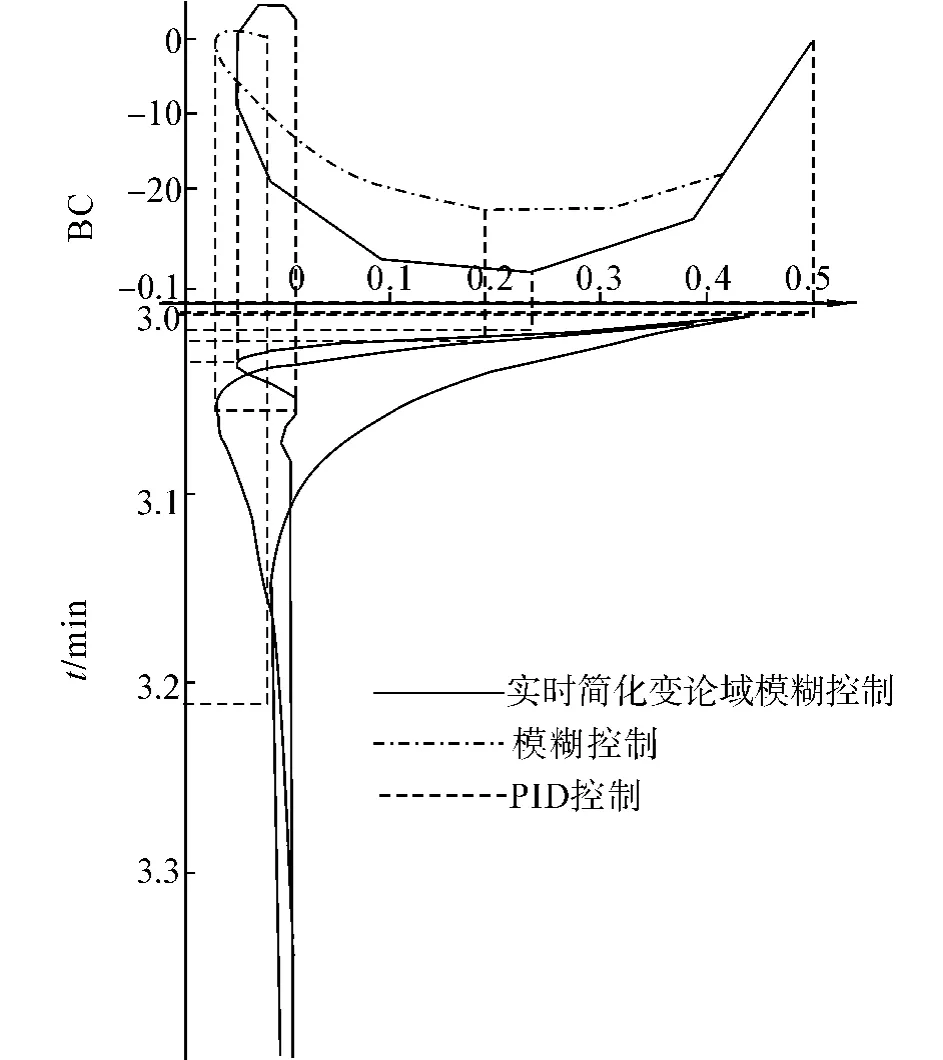
图8 3种控制方法的相平面分析Fig.8 Phase plane analysis of three control methods

6 结束语

本文建立了酸碱中和pH值控制系统的数学模型，分析了控制难点，设计了一种实时简化变论域的模糊控制算法并进行了仿真研究.通过和普通模糊控制方法及PID控制方法相比较，证实本文的方法简单、实用、控制效果好，非常适合对实时性和精确性要求都比较高的场合.变论域配合实时推理，再加上控制规则的形式不变性，使得这种方法可采用批处理的方式进行控制器设计，也可以应用于其他的单入单出的非线性系统的控制中.针对本文的内容还可以开展后续的研究工作.主要有以下2个方面:1)研究控制规则的减少对稳定性的影响;2)研究控制参数的最优设计.

［1］赵彦华，麻红昭.一种用于pH值控制的非线性系统的实现［J］.工业仪表与自动化装置，2004，3:40－43.

ZHAO Yanhua，MA Hongzhao.A new nonlinear system designed for use with pH control［J］.Industrial Instrumentation ＆ Automation，2004，3:40－43.

［2］HADJISKI M，BOSHNAKOV K，GALIBORA M.Neural networks based control of pH neutralization plant［C］//2002 First International IEEE Symposium on Intelligent Sys－tems.Varna，Bulgaria，2002:7－12.

［3］MUTHU R，KANZI E E.Fuzzy logic control of a pH neutralization process［C］//ICECS－2003.Sharjah，United Arab Emirates，2003:1066－1069.

［4］RESENDE P，ZARALE－GALVEZ L E.Control of a pH process using variable structure regulator and Smith predictor［C］//IECON’91.Kobe，Japan，1991:2102－2106.

［5］ALVAREZ T，TADEO F，GRIMBLE M J.Tuning of predictive controller using performance assessment measures:application to pH control［C］//Proceedings of the 2002 IEEE International Conference on Control Applications.Glasgow，UK，2002:403－408.

［6］TONG S W，LIU G P.Real－time simplified variable domain fuzzy control of PEM fuel cell flow systems［J］.European Journal of Control，2008，14(3):223－233.

［7］侯传嘉，张燕群.pH值测量［M］.北京:中国计量出版社，1993:7－44.

［8］石红瑞，马智宏，孙洪涛.基于多模型切换的pH自适应控制［C］//第五届全球智能控制与自动化大会.杭州，2004:488－491.

SHI Hongrui，MA Zhihong，SUN Hongtao.pH adaptive control based on multiple model switching approach［C］//Proceedings of the 5th World Congress on Intelligent Control and Automation.Hangzhou，China，2004:488－491.

［9］LI H X.Variable universe adaptive fuzzy controller［J］.Sci China Ser E－Technol Sci，1999，20:32－44.

［10］LI H X.Variable universe stable adaptive fuzzy control of a nonlinear systems［J］.Comput Math Appl，2002，44:799－815.

［11］HUANG Y，YU Y Q，ZENG T.A new real－time self－adaptive rule modification algorithm based on error convergence in fuzzy control［C］//IEEE Conference on Industrial Technology.Hong Kong，China，2005:789－794.

［12］丛爽.神经网络、模糊控制及其在运动控制中的应用［M］.合肥:中国科学技术大学出版社，2001:86－134.

佟世文，男，1976年生，高级工程师，博士，主要研究方向为欠驱动系统、网络化控制、燃料电池的建模与控制，发表学术文10余篇，获得发明专利一项.

Design and performance analysis of a pH variable domain fuzzy control system

TONG Shiwen
(China Tianchen Engineering Corporation，Beijing 100029，China)

The real－time simplified variable domain fuzzy control method for the control of a pH nonlinear system was proposed.The method combined the idea of variable domain with the real－time fuzzy inference strategy.On the one hand，the method increased the control accuracy by the contraction of the domain following the decrease of errors，which is equivalent to the increase of the control rules.On the other hand，the algorithm activated at most four control rules during each control cycle by using the real－time fuzzy reasoning method for a typical two－input one－output fuzzy controller.The consideration of the two ideas simplifies the design of the control rules，accelerates the dynamic response，and improves the control accuracy.The controller can be designed in a batch mode.The simulation results confirm that the method is effective.

pH system;variable domain;real－time fuzzy inference;fuzzy controller

TP273.4

A

1673－4785(2011)04－0367－06

10.3969/j.issn.1673－4785.2011.04.015

2009－12－01.

国家自然科学基金资助项目(60774007).

佟世文.E－mail:sun21st@sina.com.