谱图聚类算法研究进展

李建元，周脚根，关佶红，周水庚

(1.同济大学 计算机科学与技术系，上海 201804;2.上海市农业科学院 数字农业与工程技术研究中心，上海 201106;3.复旦大学上海市智能信息处理重点实验室，上海 200433)

谱图聚类算法研究进展

李建元1，周脚根2，关佶红1，周水庚3

(1.同济大学 计算机科学与技术系，上海 201804;2.上海市农业科学院 数字农业与工程技术研究中心，上海 201106;3.复旦大学上海市智能信息处理重点实验室，上海 200433)

近10多年来，关于谱图聚类的研究成果非常丰富，为了总结和理清这些工作之间的脉络关系，揭示最新的研究趋势，回顾和比较了典型的图割目标函数，以及这些目标函数的谱宽松解决方法，总结了谱聚类算法的本质.另外，讨论了谱图聚类的几个关键问题:相似图的构建方法、复杂性与扩充性、簇数估计、半监督谱学习等.最后，展望了谱图聚类算法的主要研究趋势，如探寻其理论解释，构建更贴切的相似图，通过学习筛选特征，应用实例化等.

谱图聚类;图割目标函数;谱宽松方法;相似图构建;半监督学习

聚类技术是探测数据分析的关键步骤，具有非常重要的科学地位和应用价值.传统的聚类算法如K－means［1］和 EM［2］等，它们虽然简单，但缺乏处理复杂簇结构的能力，并可能陷入局部解.近10余年来，谱聚类算法作为一种有竞争力的技术，成为一个新的研究热点，与之相关的研究成果也颇为丰富.

谱聚类是一类基于图论的聚类算法，其算法框架一般包括两大步:首先构造一个相似图用以描述数据点之间的相似关系;然后根据某个优化目标将图分割为若干不连通的子图.子图中包含的点集被视为簇.以聚类为目的的图割优化目标通常均为NP离散最优化问题，谱聚类的提出使得问题可以在多项式时间内求解.较之K－means等传统算法，谱聚类还具有另一优势:它可以处理更为复杂的簇结构(如非凸数据［3－4］)，并找到全局宽松解.故而，谱聚类已被推广应用到许多领域，如计算机视觉［5－8］、集成电路设计［9］、负载均衡［10－11］、生物信息［12－15］、文本分类［16－17］等.

谱聚类技术可以从以下几个角度进行分类:1)从是否考虑样本外扩展的角度，可以将其分为离线谱聚类(如文献［3，5，18－19］等)和增量谱聚类(如文献［20－21］等);2)从是否具有约束条件或者先验知识的角度，可以将其分为无监督谱聚类和约束谱聚类(如文献［22］等);3)按优化目标的个数可以将其分为单目标优化(绝大多数)和双目标优化(如文献［23］等);4)从运行环境上，可将其分为串行谱聚类和并行谱聚类(如文献［24］等).

迄今为止，谱聚类技术已经得到长足的发展，总结和理清已有研究之间的关系，揭示未来的研究方向是十分有必要的.已出现的综述文章各有侧重.Verma等人［25］主要从实验的角度比较了几种典型的谱聚类算法的性能，并提出若干改进算法.Luxburg等人［26］从统计学习的理论高度比较了典型的归一化和非归一化谱聚类算法，并总结了相似图构建方法和簇数估计等问题.Maurizio等人［27］调查了基于核的聚类方法和谱方法，并得出这2种方法的共同本质是迹最优化问题.国内方面，关于该领域较好的综述如文献［28］，其从算法层面上较为全面地进行了比较.

本文尽管与上述综述文献在内容上有一些重叠之处，但却包含了一些新的内容.一方面，涉及的内容更全面、脉络关系更清楚，如从图论到代数分割特性的发展、从图割目标函数到谱图聚类算法的演变、谱图聚类算法的本质等.另一方面，讨论的问题更深入，如图的构建、边权的度量、簇数的估计、复杂性与扩充性、半监督谱学习.最后，总结了有待澄清的一些的理论和实际问题，指出了谱图聚类算法的研究趋势.

1 基本理论

1.1 图论与代数图论

图论是数学的一个重要分支，是以1736年大数学家欧拉关于Konigsberg七桥问题的论文为里程碑开始发展的.它研究的是关于图(graph)的理论和方法.简单来说，图是点集和边集或弧集构成的图形，其中边或弧用来表示一对节点间存在某种关系，边或弧可以赋予权值，权值用来量化节点之间的关系.根据是否加权，图可分为无权图和加权图;根据边是否具有方向，可将图分为有向图和无向图.

常用的图的表示方法有邻接矩阵(记作A)和拉普拉斯矩阵(记作L).无权图的邻接矩阵表示法如图1(a)、(c)所示，用0表示一对顶点间无边，用1表示一对顶点间存在一条边.加权图是用某个实数来反映顶点之间关系之不同，如图1(b)、(d)所示.拉普拉斯矩阵L=D－A，其中D为对角阵，对角线上的数值等于A的行和的绝对值，非对角元素为0.关于图论的基本知识，可参考最新版图论教程［29］.

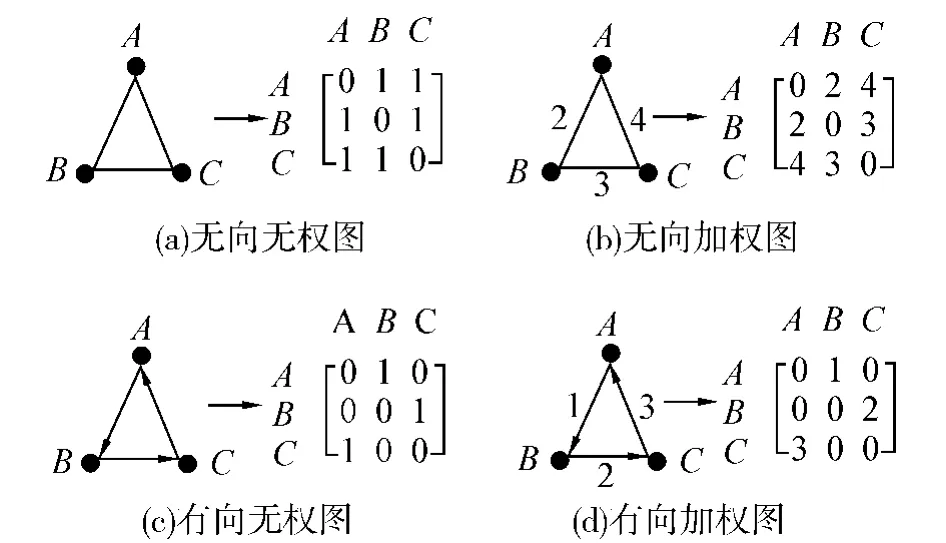
图1 图及其邻接矩阵Fig.1 Examples of graphs and adjacent matrices

代数图论是图论、线性代数以及矩阵计算理论相结合的交叉领域，其研究较早始于19世纪50年代.它是图论的分支之一，旨在利用代数方法来研究图，将图的特性转化为代数特性，然后利用代数特性和代数方法推导关于图的定理.事实上，代数图论的主要内容是图的谱，粗略地说，谱指的是矩阵的特征值连同其多重解(multiplicites).最早的关于代数图论的研究如:Fiedler［30］得出了图的连通性的代数判据，即根据拉氏矩阵的第二小特征值是否为零可以判断图是否连通，与第二小特征值对应的特征向量后来被命名为Fiedler向量，它包含了二分一个图所需要的指示信息.另外，Donath 和 Hoffman［31］、Bames［32］和 Donath［33］等的理论工作建立了图的谱和图割之间的另一些关联.关于代数图论较全面的介绍可参考文献［34－36］.

1.2 矩阵与谱

大多数的谱聚类算法是基于拉普拉斯矩阵(以下简称“拉氏矩阵”)的谱来进行的.拉氏矩阵分为非归一化的(L)和归一化的2种.归一化的又包括对称方式(记作Ls)和随机游走方式(记作Lr)，表达式分别如下:

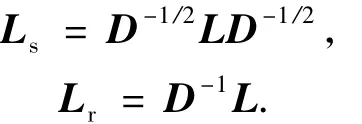
文献［37－38］给出了非归一化拉氏矩阵的部分特性，文献［36］进一步给出了归一化拉氏矩阵的部分特性.拉氏矩阵的谱对于图的分割提供了极为有用的信息，例如，基于Fiedler向量［30］可直接进行图的二分，基于多个主要特征向量可以进行图的k分.关于拉氏矩阵的特性，Luxburg［39］对其进行了较全面的概括，在此不再赘述.关于到底应该采用非归一化拉氏矩阵还是归一化拉氏矩阵的问题上目前存在着较大的分歧.采用归一化拉氏矩阵的如文献［5，23，40］，非归一化拉氏矩阵的如文献［41－42］.从实证的角度上，文献［3，5，43］提供了归一化拉氏矩阵更适用于谱聚类的证据，即意味着归一化谱聚类性能比非归一化谱聚类好.文献［44］指出在某种特定的条件下采用非归一化谱聚类较好.而文献［26］从统计一致性的理论高度，证明了归一化拉氏矩阵优于非归一化拉氏矩阵的事实.

另一种可选的矩阵是概率转移矩阵(记作P).概率转移矩阵实质上就是相似矩阵的归一化形式，其表达式如下:

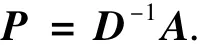
由于归一化后的相似矩阵的行和为1，因此P中的元素可以理解为马尔可夫转移概率.2个节点间的转移概率越大，则同簇的可能性也越大.概率转移矩阵的谱也包含了分割图所需的必要信息，只不过与拉氏矩阵谱稍有区别，例如，次大特征值的特征向量可以指示图的二分，多个主特征值的特征向量可以指示图的k分割.有趣的是，如果λ是Px=λx的解，则1－λ 是方程 Lx=λDx的解［45］.

值得一提的另一种新颖矩阵是模块度矩阵(记作 B).其相关研究主要出自复杂网络社区［46－49］，它具有明显物理意义，其表达式如下:

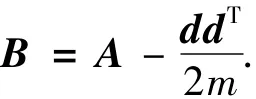
式中:d代表列向量，其元素为节点的度;m表示图的总边权;B中的元素表示的是成对节点间实际的边数与期望的边数之差，或者说是实际的边数超出期望边数的程度.因此，此类矩阵也直接促成了一个目标函数，即最优分割应使得各社区中(与“簇”相对应)边的稠密程度尽量超出预期.就矩阵特性而言，模块度矩阵与拉氏矩阵具有相似之处，例如:行和(列和)为0，0是其特征值;但又具有明显区别，模块度矩阵不是一个半正定矩阵，也就是说其部分特征值可能为负.就分割图方面，基于其最大特征值的特征向量可以进行网络二分，基于多个主特征向量可以进行网络k分.

2 主要的图割目标函数

图割聚类的雏形是最小生成树方法(minimum spanning tree，MST)［50－51］.之后出现的目标函数有最小割(minimum cut，Mincut)［32，52－53］、比率割(ratio cut， Rcut)［40，54－56］、 规 范 割 (normalized cut，Ncut)［5，57］、最 小 最 大 割 (max flow/min cut，MMCut)［58］和平均割(average cut，Acut)［59］等.除此以外，还有一些其他的优化目标，如用谱宽松来解决K－means目标函数的方法［60］，以及文献［23］提出的双准则方法.

最小生成树(MST)聚类法是 Zahn［50］提出的，该算法首先由图的邻接矩阵得到最小生成树，然后从最小生成树中去除掉若干权值较大的边从而产生一个连通分量集，以此达到聚类的目的.该方法在探测明显分离的簇时是成功的，但若改变节点密度，其性能会变差.另一个缺点是，Zahn的研究是在事先知道簇结构(如分离簇、接触簇、密度簇等)的前提下进行的.

图的割是指去除一定的边将一个图分割为多个连通分量，其中被去除的边权的总和称为割(如式(1)所示).Bames［32］最早提出了最小割聚类准则，即在把一个图分割成k个连通子图时，寻求割的最小化.Alpert和Yao［18］较早提出了基于谱方法来解决最小割准则的方法，为后来的谱聚类的发展奠定了重要基础.Wu 和 Leahy［53，61］将最小割运用到图像分割领域，并基于网络最大流理论［62］来求解最小割.该准则在图像分割方面有些许成功的应用，但其最大的问题是可能会导致分割的严重不均衡，如分割出“孤点”及“小簇”.能够产生较均衡的分割的研究有 Wei和 Cheng［40］提出的比率割、Shi和 Malik［5］提出的规范割、Ding等人［58］提出的最小最大割和Sarkar等人［59］提出的平均割，其目标函数分别为式(2)～(5).这些优化目标能够较好地避免最小割造成的分割严重不均衡的问题.

以图的二分割为例，令V为一个给定的点集，N表示V的一个子集，用M代表VN，w(·，·)表示2个点集之间边的总边权，则有:

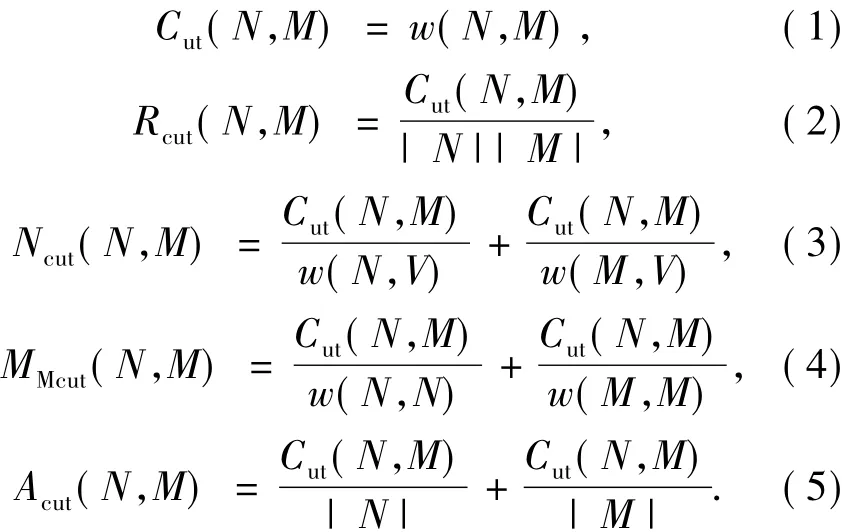
近10年来复杂网络的研究快速崛起，Newman系统地研究了无权网络、加权网络乃至有向网络中的网络社团结构谱算法，运用了模块度(modularity)函数进行社团发现［46－49］.模块度准则的思想较为新颖:以无权图为例，当各社团中的边的比例尽可能地超出“期望”的边的比例时，才认为是合理的分割.其中“期望”的边数指的是根据配置模型得到的一种随机图模型.这显然与传统的图割聚类方法的出发点不同，其目标函数为

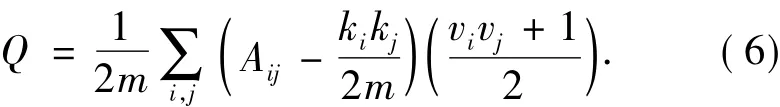
式中:Q表示模块度;m表示图中包含的边数;ki表示编号为i的节点的度(kj类似);vi和vj只可取－1或1，当vi≠vj是表示将节点i和j划分到不同社区，反之则属于同一社区.

3 谱宽松方法解决图割问题

最小化比率割、规范割、平均割以及最大化模块度等，均为NP离散最优化问题.幸运的是，谱方法可以为该最优化问题提供一种多项式时间内的宽松解.这里的“宽松”指的是将离散最优化问题宽松到实数域，然后利用某种启发式方法将其重新转换为离散解.下面简要介绍从目标函数到谱方法的演变［39，46，56］.

3.1 图的二分割问题

3.1.1 比率割

设比率割为c，考虑一个最小化式(2)的图的二分割问题，令|N|=pn，|M|=qn，其中p，q≥0 且满足p+q=1，簇指示向量x的元素满足:

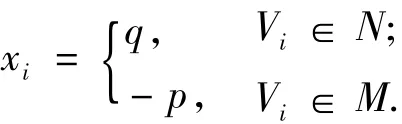
令E表示一个包含n个元素的常向量，其每个元素均设为1.因为拉氏矩阵L的各特征向量正交，而E又是L的一个特征向量，故可得x·E=0.若eij是连接N和M2个点集的边，则有xi－xj=q－(－p)=1;相反，若eij不是连接N和M2个点集的边，则有xi－xj=0.从而可得

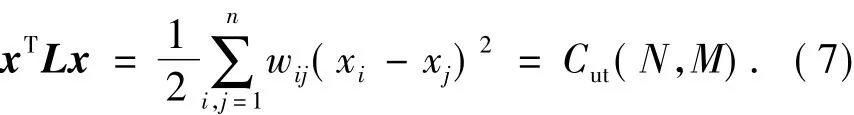
又因为

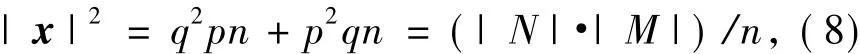
合并式(7)、(8)，根据瑞利商定理可得

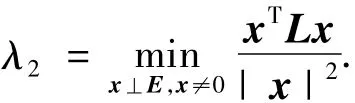
也即c≥λ2/n，这将意味着图的二分割的实数域解x由第二小特征值对应的特征向量给出，即求解方程Lx=λx，找到 λ2及其特征向量.由于聚类问题是“离散”最优化问题，故而需要将实数域解离散化，最简单的离散化方法是阈值法，即:

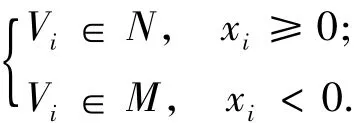
3.1.2 平均割

与上同理，令指示向量x的分量满足:

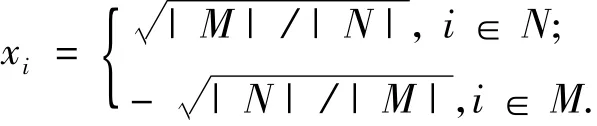
可以得出，在非归一化拉氏矩阵L与平均割之间存在如下关系:

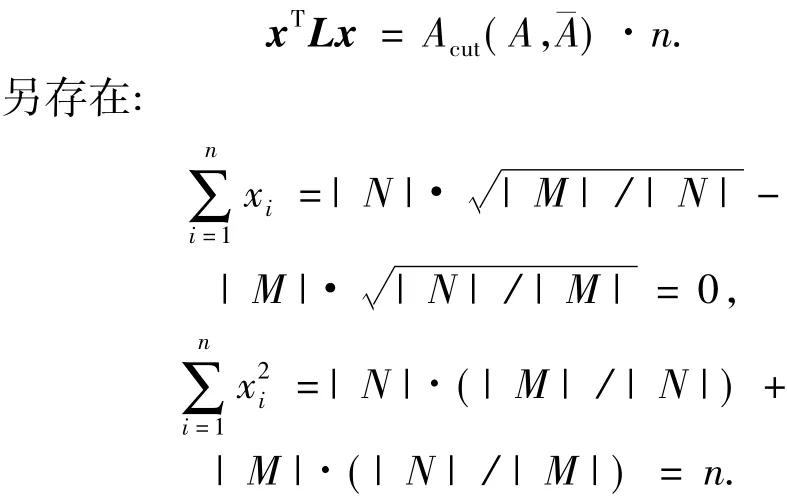
于是最小化平均割的问题与比率割的解决方法相似，需求解Lx=λx，x的离散化方法也与之类似.

3.1.3 规范割

令指示向量x满足:

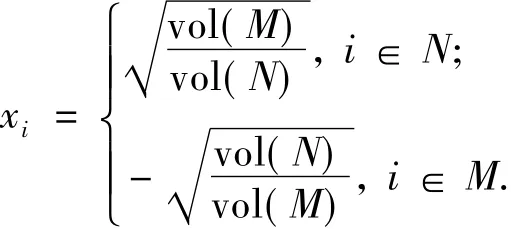
则有

又因为xTDx=vol(V)，故可得

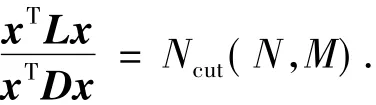
令g=D1/2x，代入上式得

因此最小化规范割相当于求解Lsx=λx或者Lx=λDx，找到归一化拉氏矩阵的第二小特征值对应的特征向量，然后将其离散化.

3.1.4 模块度

对于任意无向加权图，令w表示整个图的总权值，di代表节点i与其他节点之间的总权值.令Bij=Aij－didj/2w，v为指示向量且仅可取1或－1，当vi=vj时表示节点i与j属于同一个簇，反之属于不同的簇.用于聚类的模块度函数可表达为

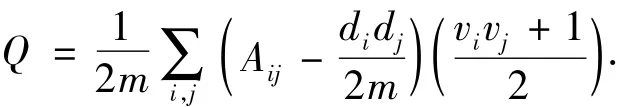
式中:w可写作w=vol(V)/2=∑ijAij，i＞j;di可写作di=vol(Vi)/=∑jAij.因为∑idi=2w=∑jdj，故存在

于是可得

即矩阵的所有项之和等于0.进一步有

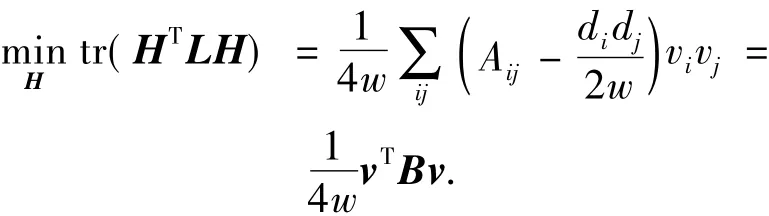
设v是矩阵B的特征向量ui的线性组合，即v=aiui，则有 ai=·v，于是有

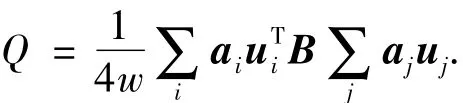
另存在关系Bv=λv，故可得

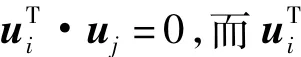
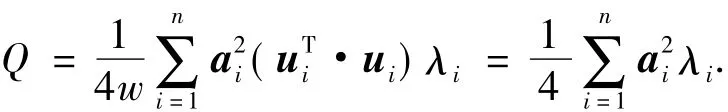
若将v的取值宽松到实数域，则可得当λi取最大特征值且v平行于其对应的特征向量时，Q取最大值.但是网络社区分割问题仍为离散最优化问题，故依然需要离散化步骤.Newman的方法是使得v的各分量与ui的各分量符号一致，也就是使二者尽量平行.

3.2 图的k分割

以平均割目标函数为例，来说明图的k分割问题的谱宽松解决方法［39］.

假定点集V可以分割为k个子集A1，A2，…，Ak，定义指示向量 hi=(h1，i，h2，i，…，hn，i)T，其中:

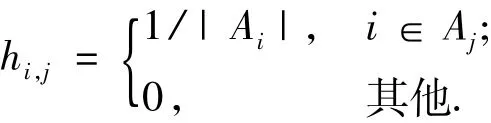
然后，令H是一个n行k列的矩阵，其列即为不同的指示向量.因为矩阵H的各列向量是相互正交的，即满足HTH=I.于是有

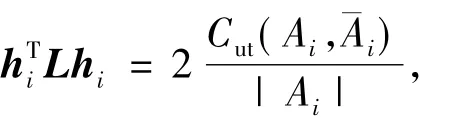
并存在

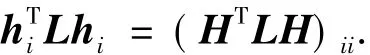
综上可得

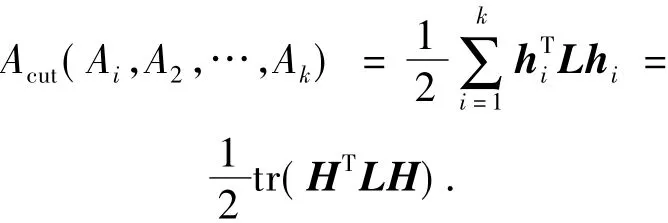
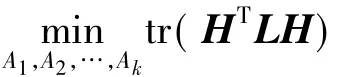
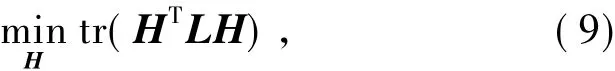
即迹最小化问题.取拉氏矩阵的前k个特征向量作为列便可得到矩阵H.然而此处H中的项在实数域中，需要离散化才能达到分类的目的.最简单的离散化方法是在实数域解H上采用K－means算法或者其他基准算法进行子空间上的聚类.

可以验证，比率割下的k分割问题与平均割的情况类似，规范割的k分割问题需要将式(9)中的拉氏矩阵L替换为归一化拉氏矩阵Ls，模块度的k分割问题需要将式(9)中的拉氏矩阵L替换为模块度矩阵B.

可见，这些最优化问题，均可运用谱方法来解决.不同的是，比率割、最小最大割、平均割派生出非归一化的谱聚类算法，而规范割派生出归一化的谱聚类算法，模块度派生出一种新的谱分割算法.然而，它们共同的本质是约束条件下的迹最优化问题［63－64］，只不过针对的矩阵不同.

4 谱图聚类中的几个关键问题

4.1 构图与加权

令wij为点i和点j之间的边权，一种最典型的加权方式是利用高斯衰减公式，即wij=exp(－‖xi－xj‖2/σ2).在给定的一个点集上建立相似图是谱聚类中最基本的问题，主要的方法如下.

1)ε 图(即阈值图):当‖xi－xj‖2＜ ε 时，相似度取0，否则取wij，其中ε为正实数.

2)k近邻图:当点i(或点j)是点j(或点i)的k个邻近点之一时，相似度取wij，否则取0.

3)互为k近邻图:当i点和j点互相落在对方的k邻域时，相似度取wij，否则设为0.

4)b－匹配图［65］:在度约束的前提下最小化图的总权值得到的一类图，可利用信任扩散方法求解其权矩阵.

5)拟合图［66］:以重构误差为优化目标，节点加权度不小于1为约束条件，利用二次规划求得的矩阵和图.

阈值图能够确保节点间的相邻关系几何对称，但阈值的选取比较困难.在一些情况下，甚至难以设定一个恰当的阈值得到一个既连通又稀疏的图.相对较好的选择应该是k近邻图，k容易选取也容易保证得到的是一个稀疏图，但是k近邻图一般是不对称的，即有向图.为了使得邻近关系对称，通常的做法是简单地消除方向.但是这样将导致连接度的不均衡性，即存在若干hub节点，从而可能对聚类问题产生一定的负面干扰.另外，互为k近邻图，虽然能保证几何对称，可以用于捕捉那些最“重要”的簇，但其缺点是不容易得到稀疏连通图(当参数k较小时).b－匹配图就拓扑结构而言是规则的，在部分场合下是优于k近邻图的，主要原因是其不存在hub节点，不会造成簇间的边过分稠密的问题;其缺点是构建一个b－匹配图时间约为O(bn3)，难以扩展其处理大规模的问题.拟合图是一种最新的研究成果，此类图能更自然地表达数据间的关系，且能从理论上保证图的稀疏性，其缺点依然是构图的时间耗费太大.

总的来看，尽管新的构图方法具有一些好的特性，但考虑到其时间耗费巨大，不及k近邻图或者互为k近邻图经济实用.近来的一些理论研究已经着眼于讨论k的界，即k大于多少时可以保证k近邻图的连通性.例如，针对包含足够多数据点的平面泊松分布数据，Xue 和 Kumer［67］证 明了 当k≥5.177 4×logn时k近邻图连通的概率为1.Balister等人［68］进 一 步 证 明 了 更 紧 的 界，即 当k≥0.513 9×logn时，k近邻图连通的概率为1.Brito等人［69］利用蒙特卡罗仿真得出了一些实证的参数，这些结果为参数k的选取提供了一定的依据.

σ是高斯核参数，许多研究者都将其设为一个全局值［3，5］，其取值范围一般满足‖xi－xj‖ ＞ σ ＞0，通过加入参数σ，将原始的相似关系映射到其他空间.考虑到机器的计算精度，过小的σ会导致相似图不连通.然而，全局设定σ的值实际上在一些情况下并不是理想的方法.文献［19］探讨了自适应设定局部参数的方式，能够更加恰当地描述节点间的邻域关系.其表达式如下:

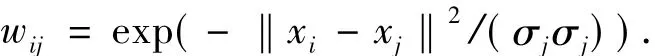
式中:σi取点i与其第K个邻近点之间的距离，σj类似.K是一个独立的参数，从几何意义上讲，它是嵌入空间的数据维数的函数，K的选取较σ更容易.该方法对于常用的人工数据(如环形嵌套的簇结构、簇间密度不同的问题等)的处理效果较好.

4.2 簇数估计问题

自动估计簇数的研究大体上可以分为2类.一种方法是通过分析特征值.文献［3］分析了在理想状况下(簇与簇之间的距离为无穷远)的簇数估计方法:对于归一化相似矩阵，特征值为1的个数严格地对应着簇数.然而实际的情况没有这么简单，一种可选的方法是分析特征值缺口(eigen－gap)［70］，在部分应用中，此方法是有效的，但是其缺乏理论根据，而且缺口往往可大可小，难以取舍.文献［71］提出将相似矩阵的特征值大于1的个数作为簇数的方法，实质上就是一种特征值缺口法.另一种更好的方法是分析特征向量，如文献［19］通过引入旋转矩阵和一个优化目标来发现最佳簇数.实验表明，该方法在一些复杂的合成数据集和图像分割应用上是有效的.

值得注意的是，以上这些方法要么是基于谱来估计簇数，要么是基于新的优化目标来估计簇数.而直接基于图割优化目标来确定簇数的研究尚少.虽然Newman［47］提出的重复二分谱算法具有这种能力，但其算法是应用在网络社区发现问题中的，在点集聚类问题上，尚需推广和验证.

4.3 复杂性与扩充性问题

快速求解稀疏矩阵的特征值和特征向量的主要算法是Arnoldi或者Lanczos算法，其他快速方法几乎都是它们的变体，关于特征空间求解方法的总结可参看文献［72］.

以非归一化谱聚类为例，即求解Lx=λx，采用Lanczos算法求解的时间复杂性分析如下.设图的总边数为m，考虑典型的稀疏矩阵(即满足m与节点数n成线性关系)，特征方程左边需要O(m)次操作，右边需要O(n)次操作，共O(m+n)次操作.再考虑上Lanczos算法的迭代次数O(n)，求解一个二分问题的时间约为O(n2).于是，重复二分谱聚类问题的时间复杂性约为O(n2logn)，解决k路谱聚类问题约为O(kn2)，空间复杂性为O(n2)，只有采用优化方法存储稀疏矩阵，才能降低其空间复杂性和时间复杂性.

一些改进的谱算法试图更快速实现该类算法.如Fowlkes等人［73］运用Nystrom近似方法避免计算整个相似矩阵，Dhillon等人［74］提出了一种不使用特征向量的方法，Yan等人［75］基于局部 K－means聚类或者随机投影树来快速近似谱聚类.这些方法虽然改善了扩充性问题，但是损失了精度，而且没有讨论空间复杂性方面的瓶颈问题.然而不论采取何种特征求解方法，当面对大规模的数据集时，都可能会遭遇空间上的瓶颈.考虑最坏的情况，也即非稀疏矩阵，设数据规模n=105，采用邻接矩阵表示法或者拉氏矩阵表示法，由于每个浮点型实数需要占据4 Byte，则大约需要占用40 GB的存储空间.

文献［24］提出了一种并行谱聚类算法，既考虑了存储空间的并行使用问题，也考虑到了并行分布式计算的问题.他们首先将n个数据实例分配到p个机器节点上，然后用最小磁盘I/O方法在每个机器节点上计算本地数据实例与所有数据实例之间的相似度.这2步与分布式特征求解和分布式参数调整结合起来，大大加速了聚类速度.其快速求解的算法采用的是较流行的ARPACK及其并行版本PARPACK［76］.通过十万数量级上的文本分类和图像分类的实证研究，表明了提出的算法有效地改善了谱聚类算法难以扩充到大规模数据集的问题.可见，若要解决大规模数量级的谱聚类问题，需要借助于并行算法.

4.4 半监督谱学习

通常，与分类问题本身无关的特征会使得大多数的谱聚类算法的性能大打折扣.几乎所有谱聚类的应用都是在某种相似性度量假设基础之上进行的，这些算法的成功依赖于度量方式的选择.而已有的大多数谱聚类算法对于不相关的特征具有较差的鲁棒性［77］.这种情况需要结合先验知识来解决，在许多情况下，某些先验知识是可以获得的，如文献［78］提及的空间一致性先验信息，文献［79］在相似性度量时依靠结合知识来减轻不相关特征造成的影响，文献［77，80］提出了从数据中自动学习的方式来确定恰当的核或者相似性度量方法，文献［77］提供了一个基于实例的相似矩阵学习的总体框架，文献［78］提出了一种从数据中学习先验知识的密度敏感的半监督聚类算法等，均取得了较好的效果.

5 结论与展望

图分割的本质可以归结为矩阵的迹最小化或最大化问题，而完成该最小化或最大化的任务需要依靠谱聚类算法.在绝大多数情况下，归一化谱聚类的性能超过非归一化谱聚类的性能，所以归一化谱聚类的应用更为广泛.它之所以吸引了大批研究者，最主要的原因有3点:1)它具有坚实的理论基础——代数图论;2)对于较复杂的簇结构，它能得到全局宽松解;3)它能在多项式时间内解决问题.近年来，在与图和网络相关的领域中，个性化的改进算法层出不穷，在某种程度上，谱聚类已经成为现代最流行的聚类算法之一.

以下提出今后依然需要探讨的几点问题.

1)谱聚类的理论解释.例如，在谱聚类中，采用哪些特征向量最好?应该采用多少个特征向量最好?为什么?采用部分特征向量张成的子空间，保留了什么信息?损失了什么信息?

2)如何更恰当地构建相似图，相似图构建的好坏决定着谱聚类性能.近来提出的b－匹配图和拟合图就是非常有趣和有用的方法，尽管已有的构建方法已经不少，但关于该问题依然需要推陈出新，最核心的一点是如何本质地描述数据之间的关系.

3)加权方式或者参数选择.虽然构图的同时已经加权，但也可以考虑重新加权的问题.例如，流形学习领域的一个重要概念“局部线性重构”［81］就是一种有效的重加权方式.再比如，高斯核参数是谱聚类中的一个非常敏感的参数，该参数选择的恰当与否直接影响着聚类的效果，关于自动选取该参数的研究是另一个难题.

4)如何将优化目标与簇数估计相结合，已有的绝大多数谱算法并不能根据其图割优化目标来决定簇数，也就是说在算法运行之前簇数是给定的.然而，在许多应用场合中，事先知道簇数是不现实的，如何在图割优化目标的指导下发现簇数是值得思考的.

5)探讨基于其他矩阵的谱聚类算法.如文中提及的模块度矩阵，它与拉氏矩阵的特性相似但又有很大区别，该算法在处理真实网络时表现出很好的性能，但是推广其用于谱聚类，依然有许多问题值得探讨.

6)如何在构建相似图的过程中进行自动特征筛选.例如:针对高维数据，L1图的构建可以有效地捕捉最稀疏的特征，从而得到非常高的聚类和分类准确性［82］.

7)如何快速解决大规模或超大规模的谱聚类问题.随着经济和社会的发展，在许多行业中，需要处理的数据规模与日俱增，虽然现有的研究已经能够解决10万数量级的问题，但是解决更大规模的问题仍然具有挑战性.

8)应用实例化.与各学科或应用领域相结合，通过改进典型的谱聚类算法切实解决实际问题.例如，在网络文档分类中，如何恰当地利用全局一致性信息，如何增量地聚类动态更新的博客社区等.

［1］LLOYD S P.Least squares quantization in PCM［J］.IEEE Transactions on Information Theory，1982，28(2):129－137.

［2］DEMPSTER A P，LAIRD N M，RUBIN D B.Maximum likelihood from incomplete data via the EM algorithm［J］.Journal of the Royal Statistical Society—Series B:Statistical Methodology，1977，39(1):1－38.

［3］NG A Y，JORDAN M I，WEISS Y.On spectral clustering:analysis and an algorithm［C］//PIETTERICH T G，BECKER S，GHAHRAMANI Z.Advances in Neural Information Processing Systems.Cambridge，USA:MIT Press，2001:849－856.

［4］RAHIMI A，RECHT B.Clustering with normalized cuts is clustering with a hyperplane［C］//Statistical Learning in Computer Vision Workshop in ECCV 2004.Prague，Czech Republic，2004:1－12.

［5］SHI J B，MALIK J.Normalized cuts and image segmentation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(8):888－905.

［6］MALIK J，BELONGIE S，LEUNG T，et al.Contour and texture analysis for image segmentation［J］.International Journal of Computer Vision，2001，43(1):7－27.

［7］ZHANG X R，JIAO L C，LIU F.Spectral clustering ensemble applied to SAR image segmentation［J］.IEEE Transactions on Geoscience and Remote Sensing，2008，46(7):2126－2136.

［8］陶文兵，金海.一种新的基于图谱理论的图像阈值分割方法［J］.计算机学报，2007，30(1):110－119.

TAO Wenbing，JIN Hai.A new image thresholding method based on graph spectral theory［J］.Journal of Computers，2007，30(1):110－119.

［9］ALPERT C J，KAHNG A B.Multi－way partitioning via geometric embeddings，orderings and dynamic programming［J］.IEEE Transactions on Computer－Aaided Design of Integrated Circuits and Systems，1995，14(11):1342－1358.

［10］DRIESSCHE R V，ROOSE D.An improved spectral bisection algorithm and its application to dynamic load balancing［J］.Parallel Computing，1995，21(1):29－48.

［11］HENDRICKSON B，LELAND R.An improved spectral graph partitioning algorithm for mapping parallel computations［J］.SIAM Journal on Scientific Computing，1995，16(2):452－459.

［12］CRISTIANINI N，SHAWE－TAYLOR J，KANDOLA J.Spectral kernel methods for clustering［C］//Proceedings of the Neural Information Processing Systems.Vancouver，Canada，2001:649－655.

［13］KLUGER Y，BASRI R，CHANG J T，et al.Spectral biclustering of microarray data:coclustering genes and conditions［J］.Genome Research，2003，13(4):703－716.

［14］KULIS B，BASU S，DHILLON I S，et al.Semi－supervised graph clustering:a kernel approach［C］//International Conference on Machine Learning.New York，USA:ACM Press，2005:457－464.

［15］PACCANARO A，CHENNUBHOTLA C，CASBON J A.Spectral clustering of protein sequences［J］.Nucleic Acids Research，2006，34(5):1571－1580.

［16］DHILLON I S.Co－clustering documents and words using bipartite spectral graph partitioning［C］//Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York，USA:ACM Press，2001:269－274.

［17］谢永康，周雅倩，黄萱菁.一种基于谱聚类的共指消解方法［J］.中文信息学报，2009，23(3):10－16.

XIE Yongkang，ZHOU Yaqian，HUANG Xuanjing.A spectral clustering based coreference resolution method［J］.Journal of Chinese Information Processing，2009，23(3):10－16.

［18］ALPERT C J，YAO S Z.Spectral partitioning:the more eigenvectors，the better［C］//Proceedings of the 32nd Annual ACM/IEEE Design Automation Conference.New York，USA:ACM，1995:195－200.

［19］ZELNIK－MANOR L，PERONA P.Self－tuning spectral clustering［C］//Neural Information Processing Systems.Vancouver，Canada，2004，2:1601－1608.

［20］NING Huazhong，XU Wei，CHI Yun，et al.Incremental spectral clustering with application to monitoring of evolving blog communities［C］//Proceedings of the SIAM InternationalConference on Data Mining. Minneapolis，USA，2007:261－272.

［21］ALZATE C，SUYKENS J A K.Multiway spectral clustering with out－of－sample extensions through weighted kernel PCA［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(2):335－347.

［22］YU S X，SHI J B.Grouping with bias［C］//The Fifteenth Annual Conference on Neural Information Processing Systems.Vancouver，Canada，2001:1327－1334.

［23］KANNAN R，VEMPALA S，VETTA A.On clusterings:good，bad，and spectral［J］.Journal of the ACM，2004，51(3):497－515.

［24］SONG Yangqiu，CHEN Wenyen，BAI Hongjie，et al.Parallel spectral clustering［C］//European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases.Antwerp，Belgium，2008:374－389.

［25］VERMA D，MEILA M.A comparison of spectral clustering algorithms，Technical Report UW－CSE－03－05－01［R］.Seattle，USA:Department of CSE，University of Washington，2003.

［26］LUXBURG U，BELKIN M，BOUSQUET O.Consistency of spectral clustering［J］.Annals of Statistics，2008，36(2):555－586.

［27］FILIPPONE M，CAMASTRA F，MASULLI F，et al.A survey of kernel and spectral methods for clustering［J］.Pattern Recognition，2008，41(1):176－190.

［28］蔡晓妍，戴冠中，杨黎斌.谱聚类算法综述［J］.计算机科学，2008，35(7):14－17.

CAI Xiaoyan，DAI Guanzhong，YANG Libin.Survey on spectral clustering algorithms［J］.Computer Science，2008，35(7):14－17.

［29］DIESTEL R.Graph theory［M］.4th ed.Heidelberg，Germany:Springer－Verlag，2010.

［30］FIEDLER M.Algebraic connectivity of graphs［J］.Czechoslovak Mathematical Journal，1973，23(98):298－305.

［31］DONATH W E，HOFFMAN A J.Lower bounds for the partitioning of graphs［J］.IBM Journal of Research and Development，1973，17(5):420－425.

［32］BAMES E R.An algorithm for partitioning the nodes of a graph［J］.SIAM Journal on Algebraic and Discrete Methods，1982，17(5):541－550.

［33］DONATH W E.Logic partitioning［M］//PREAS B T，LORENZETTI M J.Physical Design Automation of VLSI Systems.［S.l.］:Benjamin/Cummings Pub Co，1988:65－86.

［34］BIGGS N L.Algebraic graph theory［M］.Cambridge，USA:Cambridge University Press，1974.

［35］BROUWER A E，HAEMERS W H.Spectra of graphs［EB/OL］. ［2010－10－05］.http://homepages.cwi.nl/～aeb/math/ipm.pdf.

［36］CHUNG F.Spectral graph theory［EB/OL］. ［2010－10－05］.http://www.ams.org/mathscinet－getitem?mr=1421568.

［37］MOHAR B.The Laplacian spectrum of graphs［M］//ALAVI Y，CHARTRAND G，OELLERMANN O R，et al.Graph Theory，Combinatorics，and Applications. ［S.l.］:Wiley，1991，2:871－898.

［38］MOHAR B.Some applications of Laplace eigenvalues of graphs［J］.Graph Symmetry:Algebraic Methods and Applications，1997，497(22):227－275.

［39］LUXBURG U.A tutorial on spectral clustering［J］.Statistics and Computing，2007，17(4):395－416.

［40］WEI Y C，CHENG C K.Toward efficient hierarchical designs by ratio cut partitioning［C］//IEEE International Conference on CAD.New York，USA，1989:298－301.

［41］BARNARD S，POTHEN A，SIMON H.A spectral algorithm for envelope reduction of sparse matrices［J］.Numerical Linear Algebra with Applications，1995，2(4):317－334.

［42］GUATTERY S，MILLER G L.On the quality of spectral separators［J］.SIAM Journal on Matrix Analysis and Applications，1998，19(3):701－719.

［43］WEISS Y.Segmentation using eigenvectors:a unifying view［C］//Proceedings of the Seventh IEEE International Conference on Computer Vision.Washington，DC，USA:IEEE Computer Society，1999:975－982.

［44］HIGHAM D，KIBBLE M.A unified view of spectral clustering［EB/OL］.［2010－10－05］.http://meyer.math.ncsu.edu/Meyer/Courses/Selee591RPresentation.pdf，2007.

［45］MEILA M，SHI J B.Learning segmentation by random walks［C］//LEEN T K，DIETTERICH T G，TRESP V.Advances in Neural Information Processing Systems.Cambridge，USA:MIT Press，2001:873－879.

［46］NEWMAN M E J.Finding community structure in networks using the eigenvectors of matrices［J］.Physical Review E，2006，74(3):036104.

［47］NEWMAN M E J.Modularity and community structure in networks［J］.Proceedings of the National Academy of Sciences of the United States，2006，103(23):8577－8582.

［48］NEWMAN M E J.Analysis of weighted networks［J］.Physical Review E，2004，70(5):056131.

［49］LEICHT E A，NEWMAN M E J.Community structure in directed networks［J］.Physical Review Letters，2008，100(11):118703.

［50］ZAHN C T.Graph－theoretic methods for detecting and describing gestalt clusters［J］.IEEE Transactions on Computers，1971，20(1):68－86.

［51］URQUHART R.Graph theoretical clustering based on limited neighborhood sets［J］.Pattern Recognition，1982，15(3):173－187.

［52］WAGNER D，WAGNER F.Between mincut and graph bisection［J］.Lecture Notes in Computer Science，1993，711:744－750.

［53］WU Z，LEAHY R.An optimal graph theoretic approach to data clustering:theory and its application to image segmentation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1993，15(11):1101－1113.

［54］CHAN P K，SCHLAG M D F，ZIEN J Y.Spectral k－way ratio－cut partitioning and clustering［J］.IEEE Transactions on Computer－Aided Design of Integrated Circuits and Systems，1994，13(9):1088－1096.

［55］WEI Y C，CHENG C K.A two－level two－way partitioning algorithm［C］//IEEE International Conference on CAD.Santa Clara，USA，1990:516－519.

［56］HAGEN L，ANDREW B K.New spectral methods for ratio cut partitioning and clustering［J］.IEEE Transactions on Computer－Aided Design of Intergrated Circuits and Systems，1992，11(9):1074－1085.

［57］YU S，SHI J B.Multiclass spectral clustering［C］//Proceedings of the Ninth IEEE International Conference on Computer Vision.Nice，France，2003，2:313－319.

［58］DING C，HE X，ZHA H，et al.A min－max cut algorithm for graph partitioning and data clustering［C］//Proceedings of the 2001 IEEE International Conference on Data Mining.Washington，DC，USA:IEEE Computer Society，2001:107－114.

［59］SARKAR S，SOUNDARARAJAN P.Supervised learning of large perceptual organization:graph spectral partitioning and learning automata［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(5):504－525.

［60］ZHA Hongyuan，HE Xiaofeng，DING C H Q，et al.Spectral relaxation for k－means clustering［C］//DIETTERICH T G，BECKER S，GHAHRAMANI Z.Advances in Neural Information Processing Systems.Cambridge，USA:MIT Press，2002，14:1057－1064.

［61］WU Z，LEAHY R.Tissue classification in MR images using hierarchical segmentation［C］//1990 IEEE Nuclear Science Symposium Conference Record，Including Sessions on Nuclear Power Systems and Medical Imaging Conference.Piscataway，USA:IEEE Service Center，1990:1410－1414.

［62］FORD L R，FULKERSON D R.Flows in networks［M］.Princeton，USA:Princeton University Press，1962.

［63］DHILLON I S，KULIS Y B.A unified view of kernel kmeans，spectral clustering and graph partitioning，UTCS Technical Report#TR－04－25［R］.Austin，USA:Department of Computer Science，The University of Texas at Austin，2005.

［64］DHILLON I S，GUAN Y，KULIS B.Kernel k－means:spectral clustering and normalized cuts［C］//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York，USA:ACM Press，2004:551－556.

［65］JEBARA T，WANG J，CHANG S.Graph construction and b－matching for semi－supervised learning［C］//Proceedings of the 26th Annual International Conference on Machine Learning.New York，USA:ACM，2009:441－448.

［66］DAITCH S I，KELNER J A，SPIELMAN D A.Fitting a graph to vector data［C］//Proceedings of the 26th Annual International Conference on Machine Learning.New York，USA:ACM，2009:201－208.

［67］XUE F，KUMAR P R.The number of neighbors needed for connectivity of wireless networks［J］.Wireless Networks，2004，10(2):169－181.

［68］BALISTER P，BOLLOBAS B，SARKAR A，et al.Connectivity of random k－nearest－neighbour graphs［J］.Advances in Applied Probability，2005，37(1):1－24.

［69］BRITO M R，CHFIVEZ E L，QUIROZ A J，et al.Connectivity of the mutual k－nearest－neighbor graph in clustering and outlier detection［J］.Statistics ＆ Probability Letters，1997，35(1):33－42.

［70］POLITO M，PERONA P.Grouping and dimensionality reduction by locally linear embedding［C］//DIETTERICH T G，BECKER S，GHAHRAMANI Z.Advances in Neural Information Processing Systems.Cambridge，USA:MIT Press，2001:1255－1262.

［71］田铮，李小斌，句彦伟.谱聚类的扰动分析［J］.中国科学 E 辑:信息科学，2007，37(4):527－543.

TIAN Zheng，LI Xiaobin，JU Yanwei.Perturbation analysis of spectral clustering［J］.Science in China Series E:Technological Sciences，2007，37(4):527－543.

［72］HERNANDEZ V，ROMAN J，TOMAS A，et al.A survey of software for sparse eigenvalue problems［EB/OL］.［2010－10－05］.http://www.grycap.upv.es/slepc/documentation/reports/str6.pdf.

［73］FOWLKES C，BELONGIE S，CHUNG F，et al.Spectral grouping using the Nystrom method［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26(2):214－225.

［74］DHILLON I S，GUAN Y，KULIS B.Weighted graph cuts without eigenvectors:a multi－level approach［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29(11):1944－1957.

［75］YAN D H，HUANG L，JORDAN M I.Fast approximate spectral clustering［C］//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York，USA:ACM Press，2009:907－915.

［76］MASCHHOFF K J，SORENSEN D C.A portable implementation of ARPACK for distributed memory parallel architectures［EB/OL］. ［2010－10－05］.http://www.caam.rice.edu/_kristyn/parpack home.html.

［77］BACH F R，JORDAN M I.Learning spectral clustering，Technical Report No.UCB/CSD－03－1249［R］.Berkeley，USA:Computer Science Division，University of California，2003.

［78］王玲，薄列峰，焦李成.密度敏感的半监督谱聚类［J］.软件学报，2007，18(10):2412－2422.

WANG Ling，BO Liefeng，JIAO Licheng.Density－sensitive semi－supervised spectral clustering［J］.Journal of Software，2007，18(10):2412－2422.

［79］KAMVAR S D，KLEIN D，MANNING C D.Spectral learning［C］//Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence.Acapulco，Mexico，2003:561－566.

［80］FISCHER I，POLAND I.New methods for spectral clustering，Technical Report No.IDSIA－12－04［R］.Manno，Switzerland:Dalle Molle Institute for Artificial Intelligence，2004.

［81］ROWEIS S，SAUL L.Nonlinear dimensionality reduction by locally linear embedding［J］.Science，2000，290(5550):2323－2326.

［82］CHENG B，YANG J，YAN S，et al.Learning with L1－graph for image analysis［J］.IEEE Transactions on Image Processing，2010，19(4):858－866.

李建元，男，1979年生，讲师，博士研究生，CCF及ACM学生会员，主要研究方向为数据挖掘、机器学习、遥感与GIS等.

周脚根，男，1978年生，副研究员，博士，主要研究方向为空间数据挖掘和空间统计等.

关佶红，女，1969年生，教授，博士生导师，博士，主要研究方向为分布计算、数据库、数据挖掘、生物信息学等.

周水庚，男，1966年生，教授，博士生导师，博士，主要研究方向为网络数据管理与搜索、海量数据挖掘与学习、生物信息学等.

A survey of clustering algorithms based on spectra of graphs

LI Jianyuan1，ZHOU Jiaogen2，GUAN Jihong1，ZHOU Shuigeng3

(1.Department of Computer Science＆ Technology，Tongji University，Shanghai 201804，China;2.Center of Information Technology in Agriculture，Shanghai Academy of Agricultural Sciences，Shanghai 201106，China;3.Shanghai Key Lab of Intelligent Information Processing，Fudan University，Shanghai 200433，China)

Over the past decade，a huge amount of research has covered the clustering algorithms that are based on the spectra of graphs.It is essential to analyze the relationships among those works so as to reveal the research tendencies.In this paper，the typical works on topics ranging from cost functions to spectral relaxation solutions were investigated and compared in an effort to clearly reveal the essence of these algorithms.Furthermore，the focus was concentrated on several crucial technical issues，including the construction of similarity graphs，the estimation of the clusters’number，the complexity and scalability，and semi－supervised spectral learning.Finally，some open issues were highlighted for future studies，e.g.，finding more theoretical interpretations of spectral clustering，constructing better similarity graphs，selecting features via learning，and the instantiations of concrete fields.

spectral clustering;graph－cut objectives;method of spectral relaxation;construction of similarity graphs;semi－supervised learning

TP301.6

A

1673－4785(2011)05－0405－10

10.3969/j.issn.1673－4785.2011.05.004

2010－10－12.

国家自然科学基金资助项目(60873040).

李建元.E－mail:lijy79@gmail.com.