电磁波极化和天线极化的教学研究

张建华，黄 冶

(电子工程学院，安徽合肥 230037)

电磁波的极化是“电磁场与电磁波”和“天线与电波传播”课程中的一个重要的概念［1-4］。极化是电磁波中与频率、振幅和相位并列的四大要素之一，在通信、雷达信号检测、目标识别和抗干扰等方面具有重要的应用价值。

我们在教学中对电磁波极化和极化匹配的概念进行了深入研究，详细分析了教学中常见的几个容易引起误解的问题，能有效地提高课程教学质量。

1 极化匹配问题

接收天线的极化状态应与发射天线的极化状态相一致(称为极化匹配)，以期获得最大的接收能力。

假如收发天线均为对称振子，一个容易引起误解的问题是，对于图1所示的两个对称振子处于同一个平面内组成的收发系统，常有学生认为是极化失配的。由此造成在计算接收功率的Friis公式中还需再乘以极化不匹配形成的因子cos2α=sin2θ2，其中α为天线1的辐射电场矢量方向与天线2之间的夹角。当发射天线与接收天线极化不匹配时，定义极化匹配因子为:实际收到的功率与极化匹配时应收到的功率之比，极化匹配因子计算表达式为［5-6］式中，eT和eR分别是发射和接收天线电场复单位矢量，上标*表示复矢量取共轭，p的值在0到1之间。文献［4］用Poincaré球表示波的极化，其极化匹配因子的计算公式虽然与式(1)不同，但两者实质是一样的。

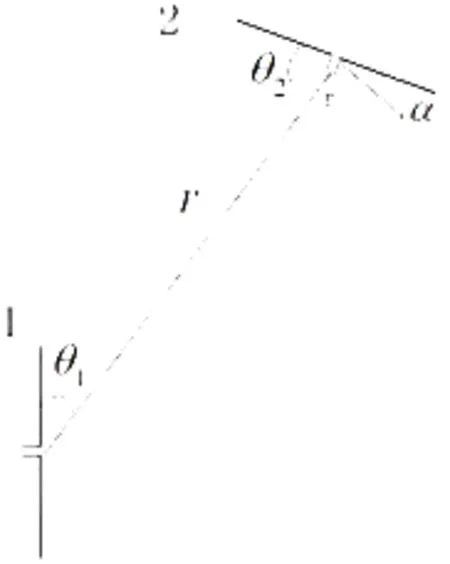
图1 线极化收发天线的共面示意图

将式(1)应用到图1所示的情况中，因为两天线共面，所以两天线的电场矢量方向一致，极化匹配因子p=1。天线的接收功率按Friis传输公式可得

式中，PT为发射天线的输入功率，GR和GT分别为收发天线的增益，FR和FT分别为收发天线的归一化方向函数。因为天线极化是匹配的，式中无需再乘以极化匹配因子p。

对于线极化天线，通过分析极化匹配因子p可以得到:p是发射平面和接收平面所构成的二面角的余弦的平方。其中，发射平面是指收发天线连线与发射天线轴线构成的平面，接收平面是指收发天线连线与接收天线轴线构成的平面。因此，发射天线与接收天线共面时，天线是极化匹配的。

2 圆极化波消除重影的问题

一般认为，采用圆极化制式的电视发射天线和用户接收天线，有助于抑制(减弱)重影现象。其依据是:当圆极化波入射到一个平面上或球面上时，其反射波旋向相反，天线只能接收旋向相同的直射波，抑制了反射波传来的重影信号。

我们知道，圆极化波可以分解为等幅、相位相差900的垂直极化波和水平极化波，而垂直极化波的反射系数与水平极化波的反射系数并不相等，因此对于圆极化的入射波，其反射波更一般的极化形式是椭圆极化。只有在垂直入射即θ=0o时，反射波的旋向才与入射波相反。因此，笼统地说采用圆极化波可消除因反射而引起的重影是不恰当的。

设电波由空气向介电常数为εr'－jεr″的媒质入射，垂直极化波和水平极化波的反射系数分别是［1-2］

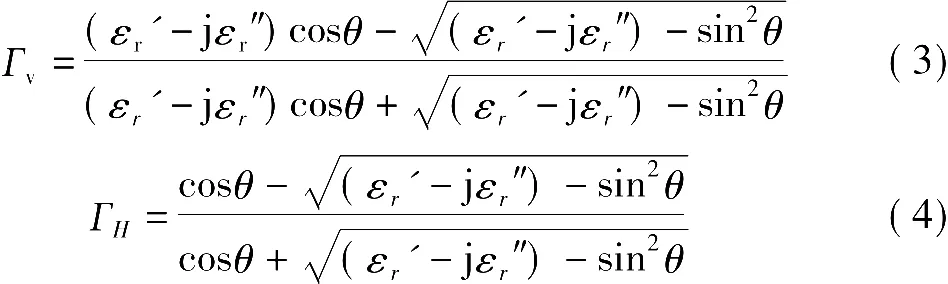
其中，θ为入射角，即入射波方向与界面法线方向的夹角。下面以水泥墙面的反射为例，文献［7］给出了水泥的介电常数和损耗正切tanδ随频率的变化曲线。在下面的计算中我们取用一组数据:εr'=10，tanδ= εr″/εr'=0.2，反射系数的模值及其相位的计算结果如图2所示。由图可见，垂直极化和水平极化的反射系数的模值和相位并不相等，垂直极化波在某个入射角(称之为布儒斯特角)时，反射系数出现极小值，该值趋于零，反射波中只有水平极化波。

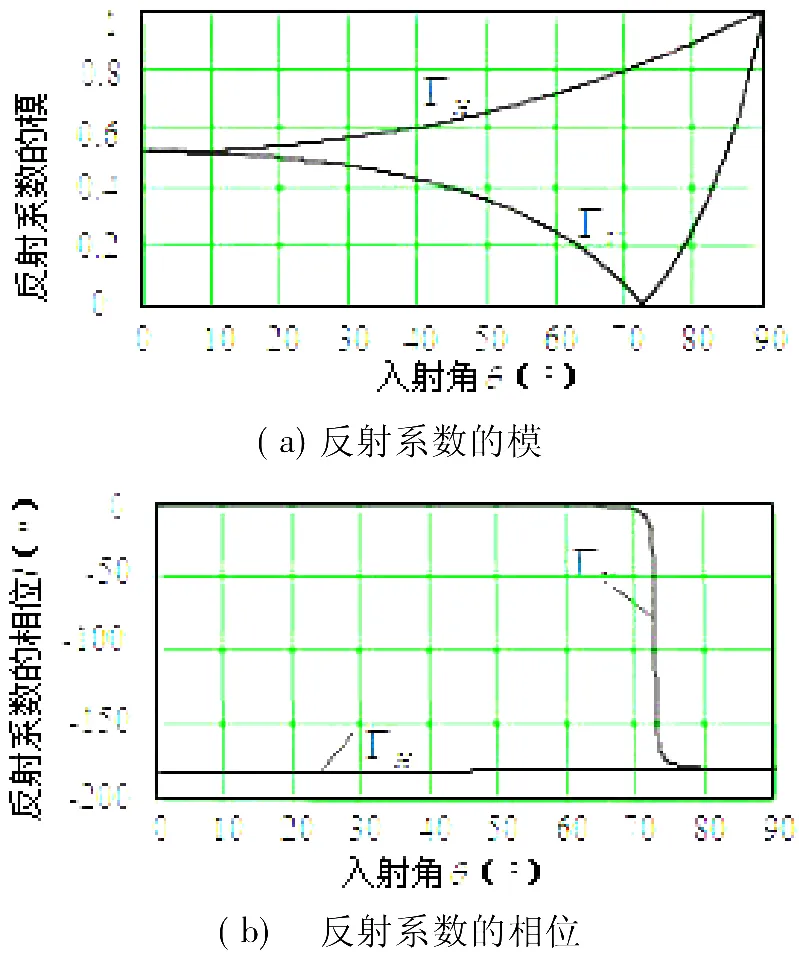
图2 垂直极化与水平极化的反射系数

下面我们来分析反射波中可被接收的同旋转方向的圆极化波有多大。假设入射的圆极化波可表示为

式中，E0为波幅，eV和eH分别为垂直极化和水平极化电场单位矢量。则反射波为

该椭圆极化波可分解为两个旋向相反的圆极化波，表达式如下:

因此可得同旋向的反射波与入射波振幅之比为

该比值v还表示接收信号中，反射波与直射波的比值，图3是v的计算结果。由图可见，入射角越小，同旋向的反射波就越小。假如以小于-10dB作为可消除反射波的判断标准的话，所对应的入射角粗略地近似为布儒斯特角。当入射角大于布儒斯特角，接收到的反射波则不可忽略。

对此结论可解释如下:因为垂直入射即θ=0o时，反射波的旋向与入射波完全相反，v很小，分贝数趋于－∞。随着入射角的增大，结合如图2(b)所示的相位，垂直极化波的反射系数的相位在布儒斯特角两侧反相，因此入射角小于布儒斯特角时，可维持相反旋向的反射波占优势。而当入射角大于布儒斯特角以后，由于垂直极化波反相，相同旋向的反射波占优势。

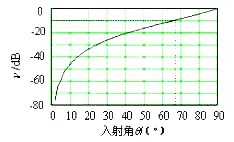
图3 相同旋向的反射波与入射波振幅之比

需要说明的是，重影的定量描述应是:经历投射—反射路径的同旋向的反射波场强与经历直射路径的直射波场强之比，还取决于两种射线路径之长度和用户接收天线之方向性函数等诸多因素，上述的判断标准非常的粗浅，主要用于说明同旋向反射波的大小。

3 圆极化波的传播

线极化波通过电离层时，会发生法拉第旋转效应，为了分析法拉第效应及其不可逆性，需要用到圆极化波的空间传播概念和图像。

利用Mathcad软件，可以画出圆极化波在某一时刻随不同传播距离的旋转情况，如图4所示。

由图可见，圆极化波随空间变量z的旋转方向与随时间旋转的方向是相反的。该现象可以从圆极化波的表达式来理解，往z方向传播的圆极化均分平面波的瞬时表达式为

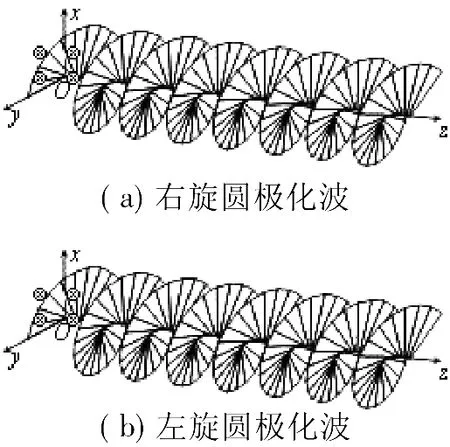
图4 极化波在同一时刻随不同传播距离的旋转情况

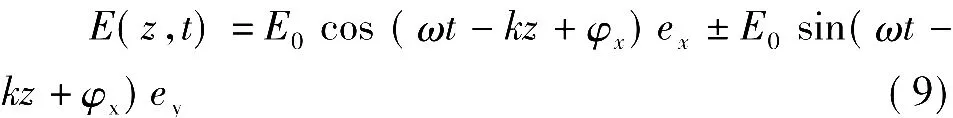
式中，“+”号对应右旋圆极化波，“－”号对应左旋圆极化波，电场矢量与x轴之间的夹角为

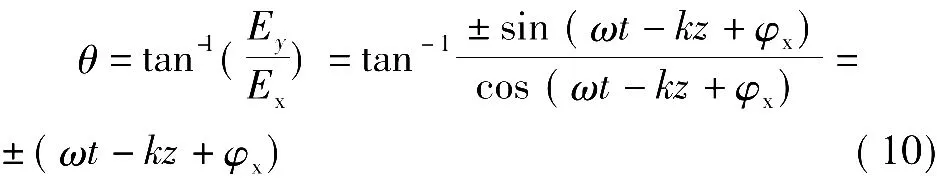
由上式可以直观地看到，圆极化波随空间变量z的旋转方向与随时间t旋转的方向是相反的。如图4(a)的右旋圆极化波，在某一固定时间，z越大圆极化的起始角度越负，而任意点上的电场随时间都是绕z轴成右手旋转关系的。

在教学中，圆极化波的传播过程用随时间和空间变化的avi格式以动态图象形式表现出来。

4 线极化波的接收

采用方向图函数为 F(θ，φ)的对称振子来接收线极化波，当来波电场方向与接收对称振子的轴线方向不一致时，如图5所示。其中来波电场矢量平行于入射面，有学生认为由于对称振子只接收到平行于振子轴线的分量Ez=Eθsinθ。因此除考虑接收天线的方向图函数外，还需要再将来波电场矢量作投影，接收的感应电动势为

其中，le为天线的有效长度。

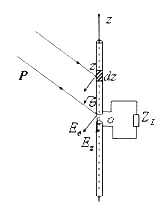
图5 接收天线的方向性分析

其实方向函数F(θ，φ)中已经考虑了sinθ因子的影响。为此，我们来深入研究天线方向性的形成因素。

形成发射天线方向性有如下三个因素。

(1)电流元的方向性

为求解天线的辐射场，可将天线分割成无限多个电流元dz，在距中心z处的电流元dz对远区场的贡献为［5］

式中，R为电流元dz到场点的距离，θ为传播方向与天线轴夹角，sinθ一是电流元的方向性，I(z)为天线上电流分布，k为波数，λ为波长。

(2)各电流元到场点的相位差

在远区，以坐标原点到场点的路径r为参考，上

式中距离R与r的关系为

式中，R与r的差异与方向θ有关。路程差不同而引起的相位差正是形成天线方向性的因素之一。

(3)电流分布

式(12)的积分结果是与电流分布有关的。

上述三个因素形成了发射天线的方向性。对于接收天线，其方向性也有三个对应的形成因素。设来波方向与天线轴之间的夹角为θ，来波电场可分解为两个分量:一个是与入射面相平行的分量Eθ，一个是与入射面相垂直的分量，该垂直分量是接收不到的，称之为正交极化分量。

形成接收天线方向性有如下三个主要因素。

(1)基本元的方向性

将接收天线分割成无限多个基本单元dz，可参考图5。只有与天线轴相平行的电场分量才能在天线导体dz段上产生感应电动势dV(z)=Eθsinθdz，因此基本元的方向性为sinθ。

(2)来波到达各基本元的相位差

接收天线位于发射天线的远区辐射场中，因此可以认为到达接收天线处的无线电波是均匀平面波，其等相位面为平面，以天线中心点为参考时，来波到达基本元dz段与到达中心点的距离差为Δr≈-zcosθ，该式与式(13)本质是一致的。

(3)接收电流

基本元dz段上的感应电动势dV将在天线接收端的负载处产生接收电流，由互易原理可知:dV在天线接收端的负载处产生的接收电流，与dV加载于天线馈电端时在天线上激励的电流相等。

以上分析表明，接收天线与发射天线其方向性的形成因素是相同的。由于接收和发射的方向图函数是相同的，因此接收时方向图函数中包含了sinθ因子的影响，故图5中感应电动势的计算公式(11)应更正为

5 电流元的极化形式

教学中常遇到有些学生认为电流元的极化形式是圆极化的，其理由是:如图6所示，在远区，电流元的电场矢量方向是^eθ方向，即在圆弧的切线方向上，轨迹是圆形的。对此问题，我们的教学对策是:引导学生重温电磁波极化的定义，让他们自己醒悟到错误所在。

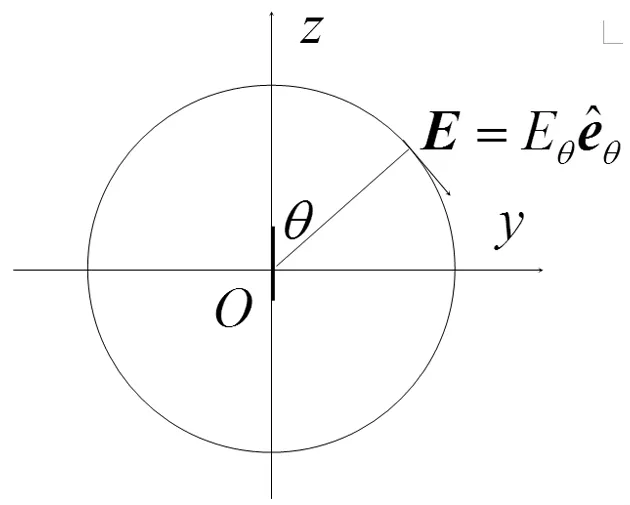
图6 电流元的电场方向

［1］ Kong J Au.Electromagnetic wave theory［M］.北京:高等教育出版社，2002

［2］ 钟顺时.电磁场基础［M］.北京:清华大学出版社，2006

［3］ 丁大志，盛亦军，樊振宏.电磁波极化理论的实验教学研究［J］.南京:电气电子教学学报，2010，32(2):55-57

［4］ 南京Kraus J D，Marhefka R J.天线［M］.第三版.北京:电子工业出版社，2006

［5］ 康行健.天线原理与设计［M］.北京:北京理工大学出版社，1993

［6］ Stutaman W L，Thiele G A.Antenna theory and Design［M］.New York:John Wiley＆ Sons，Inc.1998

［7］ 王君达，谈慕华，吴科如.无宏观缺陷水泥基复合材料的介电常数［J］，上海:同济大学学报，2000，28(2):168-171