“信号与系统”课程与解决问题能力的培养

张法全，王国富

(桂林电子科技大学 信息与通信学院，广西 桂林 541004)

“信号与系统”课程是电气信息类专业本科生的一门重要的专业基础课，以“高等数学”、“线性代数”及“电路分析”等课程为基础，是“数字信号处理”、“通信原理”、“自控原理”等后续专业课程的基础，起着承上启下的作用［1-3］。学生在学习这门课程的过程中，不但可以掌握信号、系统等重要概念和分析方法，也可以培养自己分析问题、解决问题的能力。

1 培养解决复杂问题的能力

在“信号与系统”课程中，多次讲到用基本信号及其移位信号表示任意信号的方法。如对于连续时间信号f(t)，在时域中可以用冲激信号δ(t)的移位加权和表示:

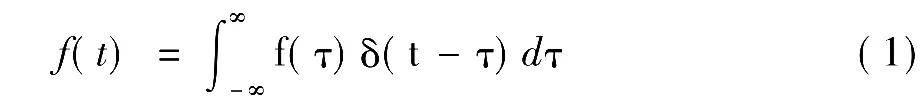
其中，δ(t－τ)是冲激信号的移位，某一时刻的函数值f(τ)作为权，积分符号相当于累加和。运用上述表达式，任意连续信号f(t)都可由冲激信号的移位加权和表示。

对于连续时间信号f(t)，在频域中可以用虚指数信号ejωt的线性组合表示为

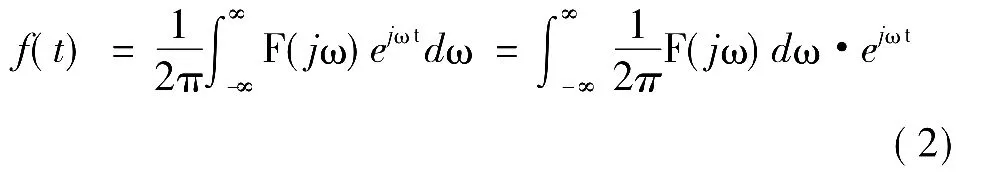
式中，(1/2π)F(jω)dω 相当于权，ejωt表示不同频率成分的虚指数信号，积分符号相当于累加和。

同样的方法也适合于离散时间信号f(n)。

如果已知基本信号对某一系统的响应，则任意信号通过该系统所产生的响应都可以求解得到。如某线性时不变系统对于单位冲激信号δ(t)的响应(即单位冲激响应)为h(t)，则根据系统的线性和时不变性，对于任意输入f(t)，利用式(1)得

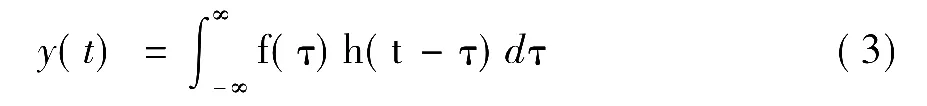
这就是该系统对任意输入的响应。

上述内容提示我们，针对某一复杂问题，可以采用分解的方法，把复杂问题分解为一系列简单问题。而简单问题一般容易解决，如果所有的简单问题都得到了解决，则复杂问题也就解决了。

2 培养解决理想与现实差距的能力

在“信号与系统”课程中，Laplace变换的引入是用于解决不满足Fourier变换条件的信号。对于单边指数信号:

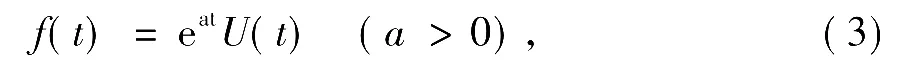
由于t→∞时，f(t)→∞，其Fourier变换不存在，只有设法变换为衰减信号，才存在Fourier变换。这就是目标与现实条件不匹配问题。此处的目标是求式(1)所示的指数信号f(t)的Fourier变换，要实现此目标则要求f(t)为衰减信号。而现有条件f(t)是指数增长信号，采用的方法是乘以一个衰减速率比原信号增长速率更快的信号，使得到的信号变为衰减信号。此处将指数增长的信号f(t)=eatU(t)(a＞0)乘以衰减因子 e－σt，当 σ ＞a时，eatU(t)e－σt就成为指数衰减信号，其 Fourier变换存在，即

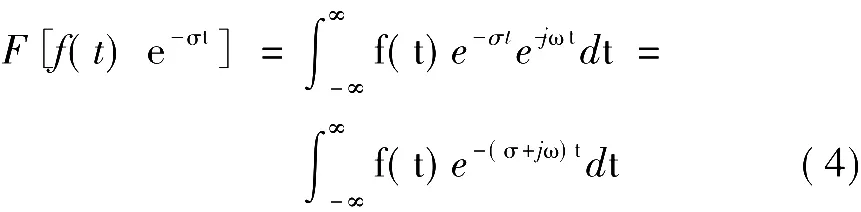
令s=σ+jω，则上式可写为

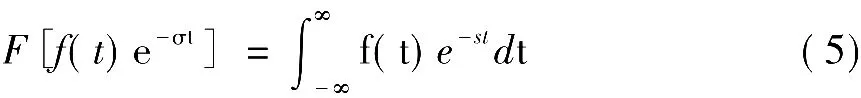
推广到一般情况，利用衰减因子e－σt乘以信号f(t)，根据信号的不同特征，选取合适的σ值，使乘积信号f(t)e－σt的幅度随着时间的增加而衰减，从而使其Fourier变换存在，引出Laplace变换:

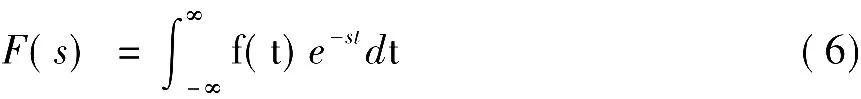
通过上述讲解过程，学生既可以很容易地从Fourier变换过渡到Laplace变换，又能从整个过程中体会到解决目标与现实条件不匹配问题的思路和方法，即如果现实条件不满足目标要求，则应增加中间过程，设法使现实条件转换为满足要求的条件，从而培养自己在这方面的能力。这种方法，同样也可以用于指导学生解决学校的条件与自己目标不匹配的问题。

3 培养从特殊到一般的思维能力

从特殊到一般的思想贯穿了整个信号与系统的课程［4-5］，上面提到的从单边增长的指数信号出发，推广到一般情况，就是一例，下面再举两例。

(1)从矩形脉冲信号总结出周期信号频谱

对于图1所示的周期矩形信号，利用Fourier级数可以求出其频谱为

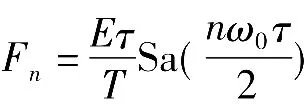
图1 周期矩形脉冲信号

通过对周期矩形脉冲信号的频谱分析，可以归纳出有关周期信号频谱的一般特点，如周期信号的频谱都是离散谱(谱线间隔为ω0)，总的趋势是递减的，信号时间特性与频率特性成相反关系等。

(2)从频域到复频域是从特殊到一般的实例

在现有理论基础上，改变问题的某一个前提条件，将问题的讨论推广到另一领域，进而得到更一般条件下的解决方法。从频域到复频域，是将一个实数域中的问题推广到复数域，从而得到更一般问题的处理方法。

4 培养综合分析问题的能力

在“信号与系统”课程内容中，连续信号与系统的频域分析、连续信号与系统的复频域分析、离散信号与系统的变换域，存在着共同的脉络，但也有各自的特点。这三部分的分析步骤是一样的，均按照正变换、变换的性质与应用、反变换及系统分析顺序进行［6］。每一部分又有各自特有的性质和作用，如Fourier变换有对偶性质。

在求解很多信号的Fourier正变换和反变换时，应用该性质可以起到事半功倍的作用。Laplace变换有单边性质，可以求解带有初始条件的系统响应。

在教学过程中，还可以将相关课程的有关问题进行比较分析，如微分方程的求解，有以下几种方法:①按照数学方法求齐次解和特殊解;②求解零输入响应，利用卷积求解零状态响应;③求解零输入响应，利用频域响应求解零状态响应;④利用复频域求解带有初始条件的系统响应。学生在分析上述内容的基础上，可以充分体验“信号与系统”介绍的分析方法的高效性，培养自己综合分析能力。

5 结语

本文从“信号与系统”的教学内容出发，探讨了学生在掌握教学内容的同时，还应努力培养自己分析问题、解决问题的能力，这既是自身能力提高的一种方法，更重要地能锻炼自己，学会思考，提高自己的综合素质。如果具备了这种能力，就能够融会贯通，把所学知识应用到实践中去。当然这种能力的培养是一个长期的过程，需要多次从理论到实践，实践再到理论的过程。同时要求教师在授课时结合教学内容，引导学生有针对性进行各种能力的培养。

［1］ 张翠芳.高等教育新形势下“信号与系统”课程的教学研究［J］.西安:西安邮电学院学报，2010，15(3).

［2］ 陈琦玮，张静亚.“信号与系统”课程教学的探索和实践［J］.北京:中国电力教育，2008，11.

［3］ 邱晓晖.“信号与线性系统”课程教学实践体会［J］.南京:电气电子教学学报，2009，31(4).

［4］ 王秀芳，高丙坤，刘霞.信号与系统课程教学的改革与实践［J］.北京:高等教育与学术研究，2010，3:27-29.

［5］ 许波，陈晓平，姬伟.“信号与系统”课程教学改革思考与实践［J］.南京:电气电子教学学报，2008，30(1).

［6］ 熊庆旭.“信号与系统”中三个层次教学探索［J］.南京:电气电子教学学报，2009，31(1).