“信号处理”课程中三种信号分析方法的比较

张海燕，方 勇，彭章友

(上海大学通信与信息工程学院，上海 200072)

小波分析、希尔伯特黄变换HHT(Hilbert Huang Transform)在数学、信号分析、地震勘探数据处理和机械故障诊断等许多领域已取得了具有科学意义和应用价值的重要成果。

在信号处理教材中，信号频谱分析的基本方法是经典的傅里叶变换。教师所教和学生所学的是傅里叶变换的定义和性质，而对其工程应用以及应用上的局限性却了解不多。我们在讲授本科生“信号与系统”和“教学信号处理”课程时，感到将傅里叶变换经典理论和最新技术相互融合是教学改革的一个方向［1］。为此本文介绍了傅里叶变换、小波变换和HHT三种频谱分析方法，利用一个简单非平稳信号，比较这三种频谱分析方法，利用新的分析方法来解决工程实际问题。

1 三种谱分析方法的特点

传统的傅里叶分析是一种纯频域的分析方法，如果一个信号函数f(t)L2(R)(R为实数)代表模拟信号，且能量有限，其Fourier变换为［1］

它用频率不同的各复正弦分量的叠加来拟合原函数，也即用F(ω)来分辨 f(t)。但是，F(ω)只能刻画f(t)在整个时间域(-∞，∞)上的频谱特征，不能反映出信号在时间的局部区域上的频率特征，特别是非平稳信号在时间轴上的任何突变，其频谱将散布在整个频率轴上。在傅立叶变换中，人们若想得到信号的时域信息，就得不到频域信息。反之亦然。

小波分析是一种窗口面积固定但时间窗和频率窗都可改变的时频局部化分析方法［2］。但这种变换实际上没有完全摆脱傅立叶变换的局限.且小波变换结果很大程度上依赖于基小波，不同的基小波得到精度不同的结果，基小波的选用往往给研究造成了一定的障碍。

HHT是1998年由Huang等提出的信号处理方法［3］。该方法适用于非平稳的信号分析，被认为是近年来对以傅立叶变换为基础的稳态谱分析的一个重大突破。但HHT在低信噪比时性能下降，在对信号用HHT分析之前，需要进行预处理以降低噪声。

HHT变换完全独立于傅立叶变换，有如下两个主要步骤:①对原始数据进行预处理，即通过EMD(Empirical Mode Decomposition)方法，把数据分解为满足Hilbert变换要求的一系列固有模式函数IMF(Intrinsic Mode Decomposition;②对分解出的每一阶IMF做Hilbert变换，得出各瞬时频率，汇总所有IMF分量得到原始非平稳信号的Hilbert谱。

2 简单非平稳信号频谱分析方法举例

本文应用上面介绍的三种方法对一个非平稳信号进行分析。我们通过对分析结果的比较，说明在信号处理中引入新方法的必要性。

假定一个频率突变的正弦信号，在1s之前的频率是10Hz，在1s之后的频率突变为20Hz，其表达式写为［4］

该信号的时域波形如图1(a)所示，该正弦信号不存在噪声干扰。从图1可以看出，Fourier谱小波变换和HHT谱一样都可以反映信号的频率特征，也即包含了10Hz和20Hz两种频率成分，但精确度却有差别。图1(b)给出了Fourier频谱。

图1(c)所示的Morlet基小波变换谱，在10Hz和20Hz附近的频率分辨率比较差。这是由于小波变换本质上是一种窗口可调的傅里叶变换，如果增加频率分辨率，便会降低时域分辨率。同时，小波变换不能脱离选择基函数的困扰，运用不同的基小波其结果也会相差很远。与Fourier谱和小波变换谱相比，图1(d)所示的HHT谱的分辨率在10Hz和20Hz处更具有频率聚焦性，分辨率较高。

图2给出了Haar和Gaussian基的小波变换谱。图2(a)中Haar小波基20Hz分量的频谱较宽，10Hz的频谱峰值只是略微能够观察到。图2(b)中10Hz和20Hz处的频谱峰值出现不同程度的偏移。与图1(c)中Morlet基小波变换谱比较可见，Morlet小波基的频谱特性较好，其频谱峰值与两个频率分量具有较好的对应性。

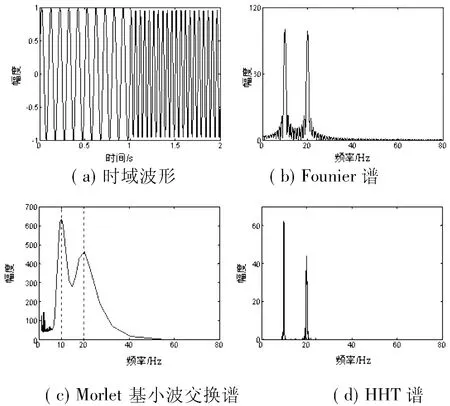
图1 正弦信号及其频谱

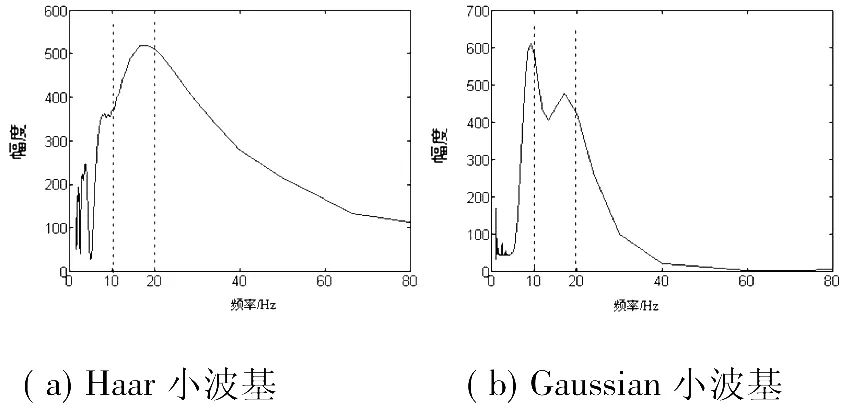
图2 正弦信号Haar和Gaussian基小波变换谱

图3给出了不同信噪比下正弦信号的HHT频谱。可以看到，低信噪比如(SNR=10dB)时 HHT的频谱严重失真，不能区分10Hz和20Hz两种频率成分。随着信噪比的提高，频谱分辨率提高，在信噪比达到40dB时即可接近理想情况。而Fourier频谱和Morlet基小波变换谱在低信噪比时只会引起旁瓣幅度增加，并没有影响两个主频分量。图4所示为信噪比为10dB时的信号频谱。

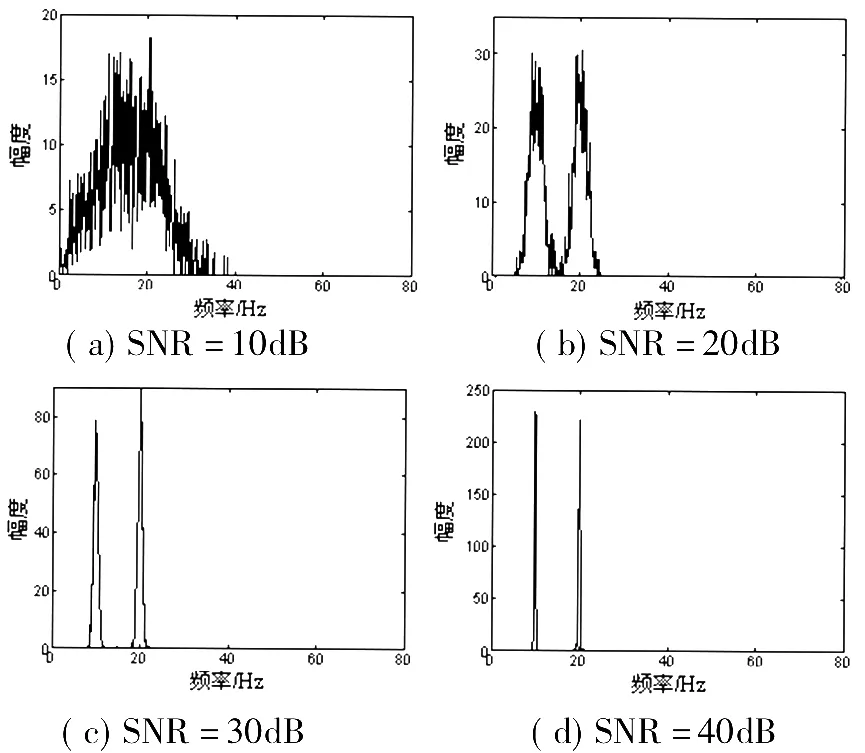
图3 不同信噪比下正弦信号的HHT谱

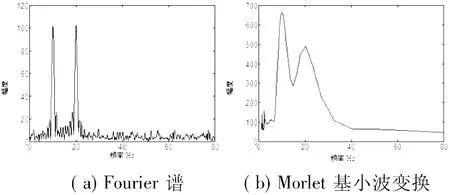
图4 SNR=10dB正弦信号的信号频谱

3 结语

教学效果成败的关键不在于学生认识和记忆了多少定义和定理，而是能否引导学生运用数学工具分析典型的物理问题［5］。本文通过一些简单示`例，使学生了解各种信号处理方法的特点以及适用性，引导学生在课堂之外关注信号处理的新方法，为其尽早进入科研领域奠定良好的基础。

［1］ 郑君里，应启珩，杨为理.信号与系统(第二版)［M］.北京:高等教育出版社，2000

［2］ 方勇.数字信号处理－原理与实践［M］.北京:清华大学出版社，2010

［3］ Huang N E，Shen Z，Long S R.The empirical mode decomposition and Hilbert spectrum for nonlinear and non－stationary time series analysis［M］.Proc.R.Soc.London.A.1998，903-95

［4］ 张海燕等.HHT在Lamb波检测信号分析中的应用［J］.南京振动、测试与诊断，2010，30(3):223-26

［5］ 郑君里.信号与系统第二版写作手记［M］.南京:电气电子教学学报，2000，22(4):61-63，82