二阶动态电路和状态方程教学的几点注记

2011-08-16关永刚于歆杰

电气电子教学学报 2011年5期

关永刚，杨颖，于歆杰

(清华大学电机工程与应用电子技术系，北京 100084)

本科“电路原理”课程教学中，动态电路是难度较大的部分。其主要原因在于求解动态电路的方法与数学联系紧密，学生往往容易死记硬背各种公式，缺乏对电路内在本质的了解和掌握。单位冲击响应、电容电压或电感电流的跳变、卷积求零状态响应、二阶电路的求解和状态方程的列写是动态电路教学中几个比较困难的知识点。本文介绍了笔者对于后两个内容的一些思考。

1 二阶动态电路时域求解的经典法

对于任意待求支路量f(t)(这里，f可以为电压u或电流i)来说，现行教材中介绍的求解过程一般是这样的:首先需要根据基尔霍夫定律(KCL和KVL)和元件约束(VCR)列写微分方程。然后求解对应的齐次方程的特征方程，得到特征根，从而确定响应形式。第三步是根据微分方程等号右端项确定方程的特解，进而获得 f(t)的通解。第四步是求 f(0+)和 f'(0+)最后根据 f(0+)和 f'(0+)确定通解中的两个待定系数，完成支路量的求解过程［1-6］。

实际教学过程中，学生往往会死记硬背上述过程，以纯数学的手段完成二阶电路的求解。这就使得“电路原理”课程在完成方程列写后缺乏物理意义，不免有些遗憾。此外，上述过程中，微分方程列写和f'(0+)求解这两个过程往往存在一定的技巧性。学生在这两个环节易走弯路。

本文就是针对这一情况，从几个方面加深学生对二阶电路物理过程和物理本质的理解，从而达到更好的教学效果。

2 二阶动态电路响应的内在联系

1)二阶动点电路响应的形式

读电路响应形式分为过阻尼、临界阻尼、欠阻尼和无阻尼四种:

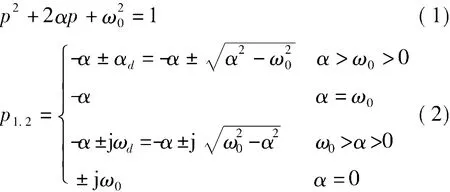
对于式(1)所示的特征方程来说，式(2)所示的四种特征根分别对应上述四种响应形式。

对于任意支路量 f(t)来说，过阻尼自由分量通解形式为f(t)=A1ep1t+A2ep2t，临界阻尼自由分量通解为 f(t)=(B1+B2t)e-αt，欠阻尼自由分量通解为 f(t)=ke-αtsin(ωdt+ φ)，无阻尼自由分量通解为f(t)=k sin(ω0t+ φ) 。其中 A1、A2、B1、B2、k 和 φ为待定系数。

表面上看，四种阻尼条件下电路通解的形式各不相同。但是，这四个表达式描述的都是二阶电路的响应特性，是否应具有某种共同的特性或内在的联系呢?

从欠阻尼状态到无阻尼状态的过渡是容易理解的。无阻尼表达式就是欠阻尼表达式在α→0时的极限情况，这一般也对应着电路中消耗能量的电阻趋向于0。这两种条件下响应的表达式无论在形式上和本质上都是统一的。

2)阻尼通解表达式关系

下面着重讨论过阻尼、临界阻尼和欠阻尼三种通解表达形式之间的关系。

以图1所示的典型RLC串联零状态二阶电路作为例。图中电源电压U=100V，电阻R=100～300Ω，电感 L=10mH，电容 C=1μF。t=0时，S 闭合。根据式(2)易知R＞200Ω时，电路为过阻尼;R=200Ω时，电路为临界阻尼;0＜R＜200Ω时，电路为欠阻尼。对该电路进行仿真，考察电容上电压uC，结果如图2所示。从波形曲线上看，在电阻R由300 Ω逐渐减小至100Ω的过程中，电路由过阻尼状态逐渐过渡到欠租尼状态，曲线过渡自然连续、没有突变。因此，各条曲线对应的数学表达式也应该是相互关联和内在统一的。

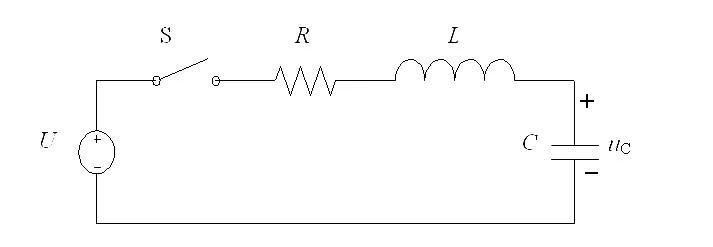
图1 RLC串联零状态二阶电路

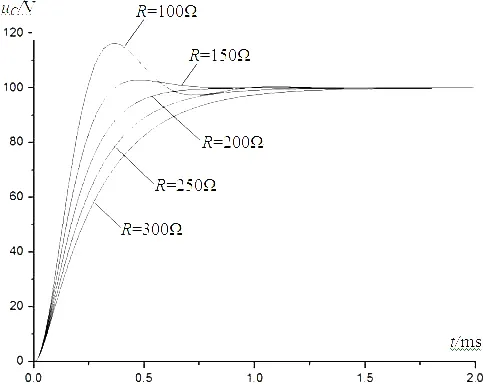
图2 不同阻尼情况下电容电压ue波形

我们先考察欠阻尼到临界阻尼的过渡。图1所示电路中，随着R增大，式(1)中的α越来越大，使得ωd→0，意味着欠阻尼的衰减震荡周期T→∞ 。

于是对于任意时间范围［0，t］来说，ωdt均可被视为属于无穷大周期正弦在t=0附近的小区域，因此可将sin(ωdt+φ)用一阶泰勒展开式替代，即写为sin(ωdt+ φ)→ ωdt。也就是说，ke－αtsin(ωdt+ φ)→ ke－αtωdt，这就是临界阻尼表达式中出现 te－αt的原因。因此，临界阻尼的表达式 B1e－αt+B2te－αt中，前者对应过阻尼的指数衰减部分，后者对应欠阻尼的衰减震荡部分。

我们还可以考察过阻尼到临界阻尼的过渡。类似地，图1所示电路中，随着R的减小，式(1)中的α越来越小，使得 αd→0。于是对于任意时间范围［0，t］来说，αdt属于在 t=0附近的小区域。因此，我们可以将 eαdt和 e－αdt分别用一阶泰勒展开式替代，即 eαdt→1+αdt和 e－αdt→1 － αdt。这样，过阻尼表达式就变成［A1(1+αdt)+A2(1 － αdt)］e－αt→［(A1+A2)+(A1－ A2)αdt］e－αt，从而顺利过渡为临界阻尼表达式。

通过上述过程，我们可讲清楚二阶电路所有响应形式之间的过渡关系。

3 列写状态方程的一般性方法

对于状态方程的列写来说，一般讲授两种方法:①根据KCL、KVL和元件约束列写数量足够的、包含状态量和非状态量的独立方程，消去非状态量，得到仅包含状态量的一阶常系数常微分方程组;②将电容看作电压源，电感看作电流源，用叠加定理求流经电容的电流和电感两端的电压，然后根据电容和电感的VCR获得状态方程。

这两种方法各有利弊。前者在列写方程和消去非状态量过程中有一定技巧性，后者转化为求解多个电阻电路，有时颇为琐碎。

从第②种方法出发，可引申出列写状态方程的一般性方法。该方法将状态方程列写与电阻电路求解紧密结合起来，学生可灵活选择求解电阻电路的各种方法以获得状态方程。

该一般性的方法其实就是在获得上述第二种方法所示电路后，不拘泥于用叠加定理求解该电阻电路，可用电阻电路的任意分析方法来求解出流经电容的电流和电感两端的电压。

下面以图3(a)所示零状态电路为例来说明，其中激励为单位阶跃函数ε(t)。

将图3(a)所示电路中电容替换为电压源，电感替换为电流源后，得到如图3(b)所示电阻电路。我们可以用求解电阻电路的任何方法来求iC和uL。这里以节点法为例参考点已标注于图3(b)中。对于节点电压u来说，有方程:

求得 u=0.25uC－0.25iL+0.25。易知 iC=-uC+u －1=-0.75uC－0.25iL－0.75，uL=u=0.25uC－0.25iL+0.25。因此，可整理出状态方程为

需要指出，节点法不一定为求解图3(b)所示电路最便捷的方法。这里仅用其说明任意方法均适用。

用该思路也适用于列写输出方程。以图3(a)中iR为例，根据图3(b)和式(3)易知

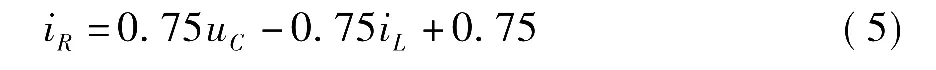
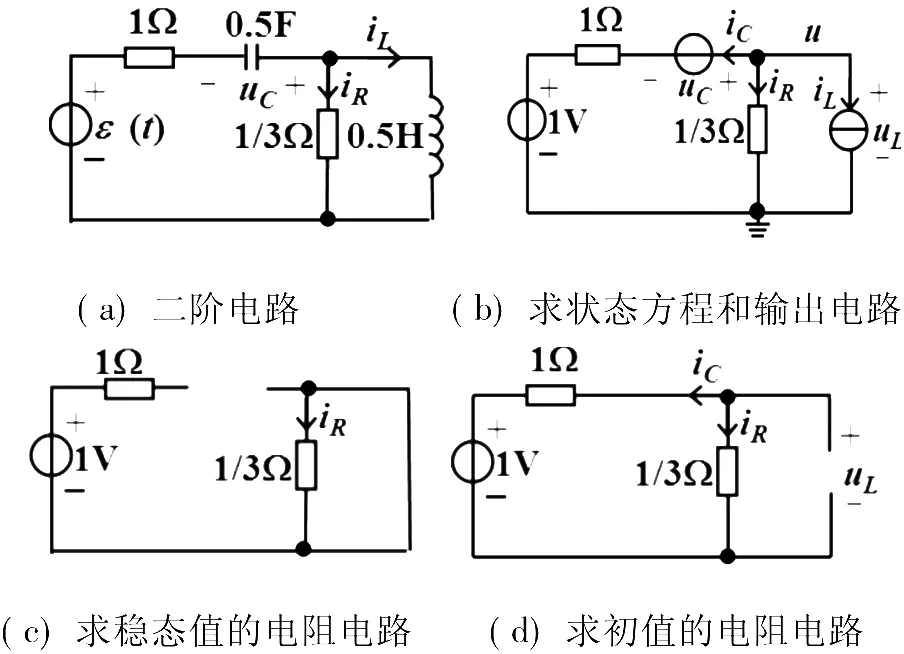
图3 状态方程和二阶例题

4 二阶动态电路求解的一般性方法

我们可根据状态方程与高阶微分方程之间内在的联系，利用状态方程列写的一般性方法，获得求解二阶动态电路的一般性方法。这里不加证明地叙述三个事实:①动态电路中任意支路量的响应形式均相同，各个支路量的区别在于稳态值、0+值和各阶导数的0+值不同;②高阶微分方程对应的特征方程就是求状态方程系数矩阵特征根所需的方程;③实际稳定的电路中由于电阻均为正值，过渡过程势必最终趋向于0，因此任意支路量的通解可写作稳态解+过渡过程的形式。

对于二阶电路来说，第1节所示经典法的难度主要在于列写任意支路量的微分方程和求解任意支路量一阶导数0+值这两步均有一定技巧性。下面我们以图3(a)所示电路为例，采用如下四步以一般性的方法来求解iR。

1)可以通过第3节所述一般性方法列写出状态方程，求其系数矩阵特征根，即可得到电路的响应形式。在本例中，根据式(4)，求解系数矩阵特征根的方程为

可求得p1=p2=-1，即该电路为临界阻尼。

2)图3(a)所示电路稳态时，等效电路如图3(c)所示(电容开路，电感短路)。易知iR(∞)=0。因此，iR的通解为

3)求取0+值。由于图3(a)所示电路为零状态电路，容易画出其0+时刻等效电路如图3(d)所示(电容短路，电感开路)，可求得iR(0+)=0.75A 。

4)求一阶导数的0+值。在第3节中我们已经求解出式(5)所示的输出方程，因此有

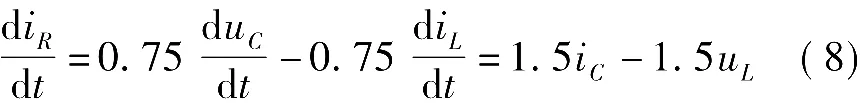
上式中，第2个等号应用了电容和电感的VCR。在图3(d)所示0+电路中容易求出iC(0+)=-0.75A，uL(0+)=0.25V，因此可知 i'R(0+)=-1.5A/s。

5)将iR(0+)和i'R(0+)代入式(7)可求出A1=0.75 ，A2=-0.75 。因此 iR=0.75(1 － t)e－1A(t＞0+)。

需要指出的是，前面讨论的方法并不一定是求解图3(a)所示电路支路量iR的最简便方法。但仔细观察整个求解过程可以发现，该方法将二阶电路求解转化为图3所示的一系列电阻电路求解，充分利用状态方程、输出方程与二阶电路支路量之间的物理联系，是一种一般性的求解方法。采用这种方法，不需要任何技巧，即可求解二阶电路中的任意支路量。在这一点上，该方法与一阶电路的三要素法具有相同的地位。此外，该方法还可以方便地扩展至正弦激励作用下的二阶动态电路。